Лабораторная работа № 4

Модульная арифметика: основы вычисления в классах вычетов

Цель работы

• Ознакомиться с использованием классов вычетов в библиотеке “FLINT\C”.

• Научиться выполнять арифметические операции с классами вычетов с использованиембиблиотеки“FLINT\C”.

Методическое указание к выполнению лабораторной работы

При делении целого числа а на натуральное число m , существует единственное представ­ление

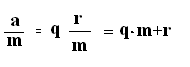
где q - целая часть числа

r - остаток от деления

Число m делит (a – r) без остатка

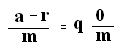
Это соотношение Гаусс предложил записывать как

a ≡ r mod m

читается оно как “ a сравнимо c r по модулю m ”;

число r называется “ вычетом по модулю m ”

Существуют определения сравнимых чисел

Определение 1. Целые чис­ла а и r называются сравнимыми по модулю m, если их разность делится без остатка на m.

Определение 2. Целые числа а и r называются сравнимыми по модулю m, если их остатки при де­лении на m одинаковы .

Все числа, сравнимые с числом r по модулю m, одинаково ведут себя при делении на m — они дают остаток r.

Объединение таких чисел в одно множест­во, называемое классом вычетов по модулю m, обозначается как ( чтобы отличить его от числа a).

Значит,- не число, а бесконечная совокупность чисел.

Все множество Z целых чисел рас­падается на m классов вычетов по модулю m.

Так, например:

Класс вычетов по модулю 5 будет включать в себя все числа

= (-10 ,-5, 0, 5 ,10, 15,……)

класс вычетов по модулю 5 будет включать в себя все числа

={-9, -4 , 1, 6 ,11 , 16,…......}

класс вычетов по модулю 5 будет включать в себя все числа

= {-8, -3 , 2 , 7 , 12 , 17, ….}

класс вычетов по модулю 5 будет включать в себя все числа

= {-7, -2 , 3 , 8 , 13, 18 …. }

а класс вычетов по модулю 5 будет включать в себя все числа

={-6 ,-1, 4 , 9, 14 , 19,……..} и т.д.

Множества чисел в классах вычетах не пересекаются, а все множество целых чисел Z можно представить как множество классов вычетов по модулю 5

Z=

Над классами вычетов по одному и тому же модулю можно проводить арифметические операции – сложение, вычитание и умножение . Результатом всех этих операций будет новый класс вычетов.

Принцип вычислений в модульной арифметике заключается в следующем: к операндам применяется соответствующая обычная («немодульная») операция, а затем результат делится с остатком на модуль.

Операция сложения опре­деляется следующим образом:

• в каждом из слагаемых классов вычетов берут по представителю, давших названия сла­гаемым класса и складывают их;

• находят вычет по модулю( остаток от деления на модуль) от полученной суммы.

Этот вычет и называют суммой данных клас­сов вычетов.

Например, сложим классы вы­четов 4 и 5 по модулю 6. Для этого возьмем сами остатки 4 и 5, давшие названия сла­гаемым классам.

• Их сумма равна 9.

• Вычет по модулю 6(остаток от деления 9/6) равен 3.

Результат 4+5=3.

Пример 2. Сложим классы вы­четов 0 и 1 по модулю 2.

• Сумма их представителей равна 1.

• Вычет по модулю 2 (остаток от деления 1/2) равен 1.

Операции вычитания и умножения выполняются аналогично операции сложения

Вычтем из класса вы­четов 1 и классы вы­четов 2 по модулю5.

• Разность их представителей равна- 1.

• Вычет по модулю 5 (остаток от деления 1/5) равен 1.

Умножим класс вы­четов 2 на класс вы­четов 4 по модулю5.

• Произведение их представителей равно 8.

• Вычет по модулю 5 (остаток от деления 8/5) равен 3.

Деление классов вычетов

Разделить класс вычетов a на класс вычетов b — значит найти такой класс вычетов х, что ах=b. Для целых чи­сел задача деления разрешима не всегда, но уж если она выполняется, то единственным образом. Это связано с тем, что произведение двух целых чисел равно нулю лишь в случае, когда хоть один из множителей ра­вен нулю. Но в F_m дело обстоит не так. Взглянув на таблицу умножения для f«, замечаем, что нули стоят в ней не только в первой строке и пер­вом столбце (там, где один из множи­телей равен нулю).

Нулю равны и произведения 2 • 3, 3 • 4, хотя множители отличны от нуля. Как говорят, в F есть делите­ли нуля (класс вычетов а называется делителем нуля, если он отличен от 0, но существует такой класс b , что а - b =0. Делителями нуля оказались классы 2, 3. 4. Числа 2, 3, 4 имеют общее свойство — они не являются взаимно простыми с моду­лем 6. Это наводит на мысль о спра­ведливости следующей теоремы:

Теорема 2. Класс вычетов а в F_m не является делителем нуля в том и только в том случае, когда а и т взаимно просты.

В случае, когда модуль является простым числом, можно делить на любой ненулевой класс вычетов — в этом случае все такие классы взаимно просты с модулем!

Примеры выполнения модульных операций

Проверка сравнимости по модулю т

Синтаксис : int mequ_l (CLINT a, CLINT b, CLINT m);

Вход: a, b (операнды), m (модуль)

Возврат: 1, если ( a ≡ b mod m )