МАТЕМАТИЧЕСКАЯ ЛОГИКА

Лекция 6. Исчисление высказываний

6.1Аксиоматизация исчисления высказываний.

6.2Формальное доказательство и формальный вывод.

6.3Свойства отношения выводимости

6.4Некоторые вспомогательные правила вывода.

6.5Полнота, непротиворечивость и независимость аксиом исчисления высказываний.

Формальные системы

Чтобы формализовать процесс человеческого мышления и создать искусственный интеллект, строятся формальные системы.

В их основе лежит алфавит, т.е. непустое конечное множество, элементы его называются символами. Любая упорядоченная последовательность символов называется словом. Построение формальной системы начинается с того, что отбираются исходные слова в той или иной предметной области. Эти начальные слова называются аксиомами. Потом формулируют правила, с помощью которых из аксиом получаются слова, которые называют теоремами. Процесс получения теорем из аксиом с помощью правил вывода можно записать в виде последовательности. Она называется доказательством теоремы. Исчисление высказываний - пример формальной аксиоматической теории.

Алфавит исчисления высказываний состоит из логических переменных, которые будем обозначать большими буквами латинского алфавита (возможно с индексами), из логических связок¬ и круглых скобок. Понятие формулы исчисления высказывания дается так же, как и в алгебре высказываний.

Формальные системы

Под формальностью понимается соблюдение ряда принципов, таких, как педантизм (всё, что

делается в системе, подчинено строго

определённым правилам), принцип явного описания (все условия применения правил и

действия, которые надо совершить при их применении, формализуются явно).

Правила формальной грамматики рассматривают правила вывода как элементарные операции, которые применяются к исходной цепочке (аксиоме) и порождают лишь правильные цепочки.

Каждый элемент (символ) алфавита принято называть буквой, а совокупность символов – словом или выражением над алфавитом А.

Например, слова ладья и лютый_мороз над алфавитом

А={а, б, …, ю, я, 0, 1, …, «,», «.», «_»}

имеют смысл в русском языке (т.е. принадлежат некоторому выделенному подмножеству F всего множества возможных слов над заданным

алфавитом и называются формулами), а слова

ълотс и 2йк,щ_ - не имеют смысла: ълотс F.

	Если пара ( f , g ), где		f f , f	,..., f		n	F,n а g F,
			1 2					илиR
находится в отношении R (т.е.					f , g
f	g	g	называется непосредст-
	R ), то формула
венным следствием			формул		f1, f2 ,..., fn или
непосредственно		выводимым		выражением из
формул f1, f2 ,..., fn		, полученным				по		правилу

вывода R.

Заданные алфавит, множество формул, аксиомы и правила вывода, т.е. совокупность

T 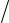A, F, P, R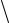, называются формальной системой (теорией) Т.

Требования, предъявляемые к формальным системам

Полнота. Если высказывание x(f), которое сопоставлено формуле f, является истинным в смысле L – языка, с помощью которого интерпретируются формулы (т.е. ν(х(f))=1 –

семантическая характеристика высказывания x(f)), то считают, что формула f выполняется в

интерпретации х.

Из аксиом должны следовать истинные высказывания, и, наоборот, для полноты нужно, чтобы все истинные высказывания модели выводились из аксиом.

Требования, предъявляемые к формальным системам

Непротиворечивость. Формальная система непротиворечива, если в ней нельзя из

некоторого набора аксиом одновременно вывести два противоречивых суждения.

Стремление математиков формализовать различные математические теории (иногда их называют математическими конструкциями) вызвано желанием найти общий метод не

только для имеющихся теорий, но и для

конструирования новых.

Если L – модель формальной теории Т

(х: F → L), то Т называется полной, если всякому истинному высказыванию из L соответствует теорема из Т, т.е.

l L : (l) 1 t x 1 (l) {h | h}├.

Независимость. Независимой системой аксиом непротиворечивой формальной теории называется такая система, в которой любая аксиома не может быть выведена на основании всех остальных аксиом этой системы.

Основные определения

Исчисление высказываний – это формальная система, позволяющая формировать новые высказывания путем указания исходных высказываний, имеющих значение «истина», а также аксиом и правил вывода, каждое из которых описывает, как формировать новое высказывание из исходных и уже построенных высказываний. Поэтому изучение исчисления высказываний следует начинать с определения аксиом и правил вывода, обеспечивающих доказательство истинности заключения.

Аксиома – это высказывание, имеющее значение истины при любых значениях пропозициональных переменных, входящих в это высказывание.

Правилом вывода называют такое отношение между высказываниями, которое позволяет из множества посылок и аксиом делать выводы об истинности заключения.

Доказательством или выводом называют такую упорядоченную последовательность высказываний, каждое из которых является либо аксиомой, либо выводимо из одного или нескольких предыдущих высказываний.

Задание необходимого числа аксиом определяет полноту исчисления, а задание правил вывода – метод исчисления.