Лаб ОДМ 1 с ПИИТС11-КНИТС 11 2012-2013 / Лаб раб 4 Распознавание свойств графов

Лабораторная работа 4

Распознавание свойств графов. Операции над графами.

1. Граф G=(V,E) представляет собой конечное множество вершин V = и некоторое множество E неупорядоченных пар вершин, называемых ребрами. Число элементов множеств V и E будем обозначать соответственно через n и m. В дальнейшем для удобства будем предполагать, что вершины графа перенумерованы и имя вершины совпадает с её номером, т.е. V={1, 2, …,n}.

Граф, имеющий конечное множество вершин называют конечным.

Вершины, соединённые ребром, называются смежными. Рёбра, имеющие общую вершину, также называются смежными. Ребро и любая из его двух вершин называются инцидентными.

Рис.1. Неориентированный граф.

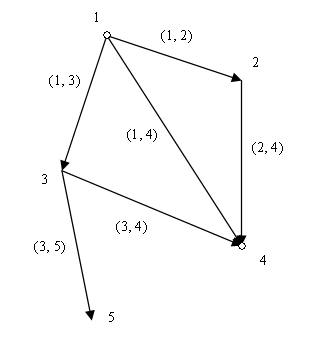
Рис.2. Ориентированный граф.

Два ребра также называют смежными, если они различны и имеют общую вершину.

Изучаются также ориентированные графы. Ориентированный граф (или орграф) – это пара G = (V, A), где V – множество вершин, A – множество упорядоченных пар элементов множества V (ориентированных ребер), которые называются дугами.

Граф G называют полным, если любые две его вершины смежные.

Граф, не имеющий ребер, называется пустым.

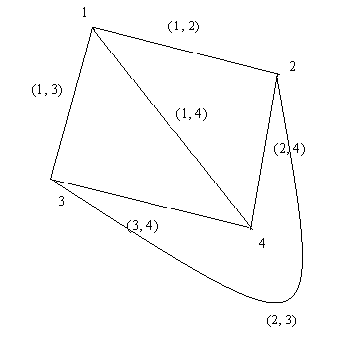
Рис. 3. Полный граф.

Рис. 4. Пустой граф.

Граф D =(R, W) называется подграфом графа G=(V,E), если и .

Подграф D называется остовным подграфом графа G, если R=V, т.е. графы D и G имеют одинаковое множество вершин.

Число рёбер инцидентных некоторой вершине x называется степенью этой вершины и обозначается через deg(x).

Два ребра вида (i, j), (i, j) называются параллельными.

Граф называется простым, если он не имеет петель − ребер вида (i, i) и параллельных ребер. В дальнейшем будем предполагать, что все рассматриваемые графы простые.

Множество всех вершин графа G, смежных с некоторой вершиной v, называется окрестностью (окружением) вершины v и обозначается NG(v) или просто N(v).

Граф G можно задавать матрицей смежности или матрицей инцидентности.

Матрица W размера nn называется матрицей смежности графа G, если W[i,j] =1 тогда и только тогда, когда вершины i и j смежны в графе G , а все остальные элементы матрицы равны 0.

Матрица W размера nm называется матрицей инцидентности графа, если

W[i,j] =

Последовательность S = смежных вершин графа G называют маршрутом. Длина маршрута равна числу рёбер этого маршрута. Например, длина маршрута S равна (k−1).

Маршрут, у которого все ребра различны, называется цепью. Маршрут, у которого первая и последняя вершины совпадают, называется замкнутым, в противном случае − открытым. Замкнутая цепь называется циклом. Цепь, у которой все вершины различны, кроме, быть может, первой и последней, называется простой. Если простая цепь замкнута, то она называется простым циклом.

Цикл графа, содержащий все его ребра, называют эйлеровым. Граф, имеющий эйлеров цикл, также называют эйлеровым.

Простой цикл графа, содержащий все его вершины, называют гамильтоновым. Граф, имеющий гамильтоновым цикл, также называют гамильтоновым.

Граф G называют связным, если любые две его вершины можно соединить цепью.

Максимальный по включению связный подграф графа называют его компонентой связности.

Граф G называют деревом, если он связный, но не имеет циклов.

Граф G называют лесом, если каждая компонента связности этого графа является деревом.

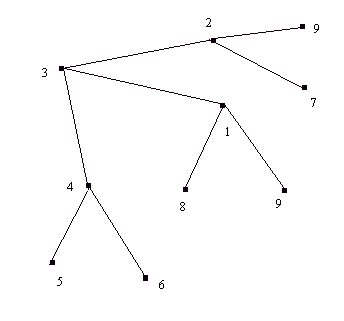
Рис.5. Граф типа дерево.

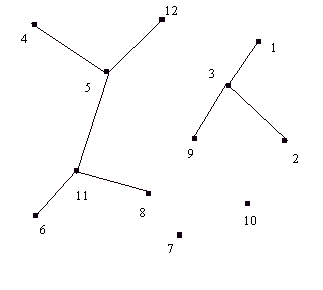
Рис.6. Граф типа лес.

Граф G называют двудольным, если множество его вершин можно разбить на два не пустых подмножества такие, что концевые вершины любого ребра принадлежат различным подмножествам.

Вершинной раскраской графа называют такое отображение (раскраску) множества его вершин в множество С={1, 2, …,k}, элементы которого называются цветами, при котором каждая вершина графа получает некоторый цвет (помечается некоторым элементом множества С). Вершинная раскраска называется правильной, если при этой раскраске смежные вершины получают различные цвета.

Граф G называют правильно вершинно раскрашиваем в K цветов, если для него существует правильная вершинная раскраска в К цветов.

Граф называют плоским или планарным, если он может быть изображён на плоскости так, что вершинам соответствуют различные точки плоскости, а линии, соответствующие рёбрам графа, не пересекаются.

Два графа G=(V,E) и D =(R, W) называют изоморфными и обозначают G D, если существует взаимно однозначное соответствие между их вершинамип, сохраняющее смежность (два изоморфных графа можно «совместить» наложением).

Опишем некоторые теоремы о свойствах графа, необходимые в дальнейшем.

Теорема 1. Конечный граф G эйлеров тогда и только тогда, когда он связан и степени всех его вершин четны.

Теорема 2. Граф G является двудольным тогда и только тогда, когда n > 1 и любой его цикл имеет четную длину.

Теорема 3. Граф G является двудольным тогда и только тогда, когда для него существует правильная вершинная раскраска в два цвета.

Теорема 4. Граф G является деревом тогда и только тогда, когда он связен и число ребер на единицу меньше числа вершин − выполняется равенство m = n − 1.

2. Над графами можно производить различные операции.

Граф называют дополнением графа G, если он имеет такое же множество вершин и две вершины смежны в тогда и только тогда, когда они не смежны в графе G.

Пусть v – вершина графа G. Тогда операцию построения графа H=G–v назы-

вают удалением вершины v: удаляется вершина v и все инцидентные ей ребра.

Пусть e – ребро графа G. Тогда операцию построения графа H=G–e называют

удалением ребра e: из G удаляется ребро e, а все вершины сохраняются.

Граф H = (R, W) называется объединением графов G=(V, E) и G= (V, E), если R = VV и W = EE. В этой ситуации пишут H = GG. Объединение H называется дизъюнктивным, если V∩V= Ø. Аналогично определяются объединение и дизъюнктивное объединение любого множества графов, причем в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.

Граф H = (R, W) называется пересечением графов G=(V, E) и G= (V, E), если R = VV и W = EE. В этой ситуации пишут H = G G. Аналогично определяются пересечение любого множества графов.

Граф H = (R, W) называется соединением графов G=(V, E) и G= (V, E), если он получается из графа GG добавлением всех ребер, соединяющих вершины V и V. В этой ситуации пишут H = G + G.

Задание

1. Выбрать произвольные два графа G=(V, E) и G= (V, E) с заданным числом вершин и ребер (в соответствии с номером в журнале), имеющие не менее двух общих вершин.

2. Для данных графов G=(V, E) и G= (V, E) построить графы: − дополнение графа G, G − получен из Gудалением вершины i, G− получен из Gудаление ребра (i, j), GG, G G, G + G.

2. Для результирующих графов, полученных в результате операций дополнения, удаление вершины и удаления ребра, построить матрицы инцидентности, а для графов, полученных в результате операций объединение, пересечение и соединение, описать их матрицы смежности.

3. Определить, какими свойствами обладают графы G, G и графы, полученные из них: , G , G, GG. Результаты описать в виде таблицы:

	Пол-ный	Пус- той	Связ- ный	Дерево	Лес	Эйле-ров	Гамиль-тонов	Дву-дольный	Плос- кий
G	*								*
G		*						*
			*
G				*
G					*
GG						*

отметив соответствующий результат знаком «+» или «−». Для клеточек, отмеченных символом «*», выводы обосновать.

Исходные данные:

Группа 1			Группа 2
	G1	G2		G1	G2
	(i,j)	(i,j)		(i,j)	(i,j)
1	(5;7)	(4;3)	1	(6;6)	(4;3)
2	(5;6)	(4;3)	2	(6;5)	(4;3)
3	(5;5)	(4;3)	3	(6;4)	(4;3)
4	(5;4)	(4;3)	4	(6;3)	(4;3)
5	(5;2)	(4;3)	5	(6;7)	(4;3)
6	(5;1)	(4;3)	6	(6;5)	(4;2)
7	(5;7)	(4;4)	7	(6;4)	(4;4)
8	(5;6)	(4;4)	8	(6;3)	(4;4)
9	(5;5)	(4;4)	9	(6;6)	(4;4)
10	(5;4)	(4;4)	10	(6;5)	(4;5)
11	(5;2)	(4;4)	11	(6;4)	(4;5)
12	(5;1)	(4;4)	12	(6;3)	(4;5)
13	(5;7)	(4;5)	13	(4;2)	(4;2)
14	(5;6)	(4;5)	14	(5;6)	(4;1)
15	(5;5)	(4;5)	15	(6;7)	(4;2)
16	(5;4)	(4;5)	16	(6;7)	(5;1)
17	(5;2)	(4;5)	17	(6;7)	(5;2)
18	(5;1)	(4;5)	18	(6;5)	(5;2)
19	(5;7)	(4;2)	19	(6;6)	(5;2)
20	(5;6)	(4;2)	20	(6;4)	(5;2)
21	(5;5)	(4;2)	21	(6;3)	(5;2)
22	(5;4)	(4;2)	22	(6;7)	(5;3)
23	(5;2)	(4;2)	23	(6;2)	(5;3)
24	(5;1)	(4;2)	24	(6;4)	(5;3)
25	(5;0)	(5;6)	25	(6;1)	(5;6)

Первый столбец − параметры графа G, второй − графа G. В паре (i, j) первое число − число вершин, второе число − число ребер.