
Теормех
.doc
|
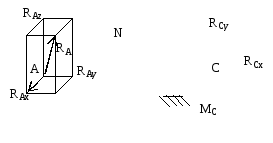
Статика – раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил , приложенных к твёрдому телу. Равновесие – такое механическое состояние тела, при котором оно находится в состоянии покоя или движется прямолинейно и равномерно. Все тела в природе взаимодействуют между собой и с окружающей средой. Сила – векторная величина, характеризующаяся величиной (модулем силы), направлением и точкой приложения. Система тел – совокупность тел, каким-либо образом связанных между собой. Внутренние силы – силы, с которыми тела данной системы взаимодействуют друг с другом. Внешние силы – силы, с которыми тела, не входящие в систему, взаимодействуют с телами данной системы. 2) Аксиомы статики А1(1 з-н Ньютона) Аксиома инерции: Тело сохраняет первоначальное состояние покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния. А2 (3 з-н Ньютона) Аксиома взаимодействия: Силы взаимодействия 2 тел равны по величине и направлены по одной прямой в противоположные стороны. А3 Условия равновесия двух сил: Для равновесия тела, находящегося под действием 2 сил, необходимо и достаточно, чтобы эти силы были равны по величине и направлены по одной прямой в противоположные стороны. А4 Аксиома присоединения: Система уравновешенных сил механического состояния твердого тела не изменит, если к нему присоединить или удалить систему уравновешенных сил. А5 Аксиома параллелограмма: Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложенных в этой же точке. А6 Аксиома затвердевания: Любое тело не изменит свое механическое состояние при переходе в абсолютно твердое. 3) Связи и их реакции. Принцип освобождаемости от связей. Основные виды связей. Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены. В любом другом случае тело является несвободным. Связи – ограничения, налагаемые на свободу любого несвободного тела. Силы, с которыми связи действуют на данное тело, называются реакциями связей. Принцип освобождаемости от связей: Всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их реакциями. Виды связей:
4) Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей. Сходящимися называются силы, линии действия которых пересекаются в одной точке. Если у такой системы сил л.д. расположены в одной плоскости, то она называется плоской системой сходящихся сил. В любом другом случае система сходящихся сил пространственная.
Равнодействующая
сходящихся сил
равна геометрической сумме этих сил
и приложена в точке их пересечения
Геометрический способ: Теорема: любая система сходящихся сил приводится к равнодействующей, равной геометрической сумме составляющих сил и приложенных в точках пересечения линий их действия. Сложность данного подхода в сложности геометрических построений. Для упрощения построений сложим геометрически силы следующим образом: конец предыдущей силы должен совпадать с началом следующего, а л.д. сил должны быть параллельны заданным. Замыкающая, полученная таким образом, и будет являться вектором равнодействующей, причем он должен быть направлен то начала к концу. Аналитический способ: Проекцией силы на ось называется направленный отрезок, заключенный между перпендикулярами, проведенными к соответствующей оси из начала к концу вектора силы. В случае пространственной системы сил используется метод двойного проецирования: сначала сила проецируется на плоскость, а затем определяются проекции полученной проекции на осях координат.
18) Теорема Вариньона о моменте равнодействующей плоской системы сил. ТЕОРЕМА: Момент равнодействующей силы относительно любой точки на плоскости равен алгебраической сумме моментов составляющих сил относительно той же точки.
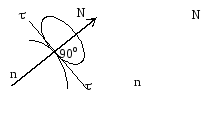
Определим момент равнодействующей силы R, приложенной в точке К, относительно произвольно выбранного центра приведения О. Мо(R)=Rh, но R=R* и h=M*/R* Тогда Мо(R)=R*/M*R*=M=M1o+M2o+…+Mno Что и требовалось доказать… 19) Статически определимые и неопределимые системы. Расчет составных конструкций. Статически определенными называют системы, которые можно решить методами статики твердого тела, т. е. системы, в которых число неизвестных не превышает числа уравнений равновесия сил. Статически неопределенными называют системы с числом неизвестных, превышающим число уравнений равновесия сил, т. е. системы, которые нельзя решать методами статики твердого тела и для решения которых нужно учитывать деформации тела, обусловленные внешними нагрузками. Если к телу приложена плоская система параллельных сил, то можно использовать только 2 уравнения равновесия сил, чтобы система была статически определена. Расчет составных конструкций. Чтобы рассчитать составную конструкцию выполняют следующие действия: 1.К конструкции прикладывают все задаваемые силы. 2. Согласно принципу освобождаемости тел от связей отбрасывают мысленно внешние связи, заменяя их соответствующими реакциями. 3. Установив, что число неизвестных реакций связей превышает число уравнений равновесия, которые можно составить для полученной системы . сил, конструкцию расчленяют, заменяя внутренние связи соответствующими реакциями. 4. Каждое из тел, входящих в состав конструкции, рассматривают как свободное, находящееся под действием задаваемых сил и реакций внешних и внутренних связей. 5. Сопоставляя общее число неизвестных величин и число всех уравнений равновесия сил, которые могут быть составлены после расчленения конструкции, устанавливают, является ли задача статически определенной. 6. Составляют уравнения равновесия сил> приложенных к каждому телу. 7. Если задача статически определенна, то полученную систему уравнений решают в наиболее удобной последовательности и определяют все неизвестные величины. 20) Распределённые нагрузки. Распределённые нагрузки: Помимо сосредоточенных сил (приложенных в точке) встречаются случаи действия на тело нагрузок распределенных по объёму, поверхности или прямой линии. Такие нагрузки называются распределенными, и они характеризуются интенсивностью q (кН/м;кН/м2;кН/м3). Распределённые нагрузки, как правило, заменяют сосредоточенными силами. Распределённые нагрузки бывают двух видов: равномерно распределённые (рисунок) Q=qe неравномерно распределённые (рисунок) Q=1/2qe 21) Трение скольжения. Законы трения. Угол и конус трения. Условия равновесия тел на шероховатой поверхности. Сила трения, возникающая при скольжении одного тела по поверхности другого называется силой трения скольжения. СТС меньше предельного значения силы трения покоя Fсц, т.к. fn чуть меньше коэффициента трения скольжения (fn˂f). F зависит только от материалов трущихся поверхностей: 0,01…0,02 – сталь по льду 0,2…0,5 – сталь по стали 0,4…0,6 – резина по асфальту 0,8 – резина по асфальту Предельное значение силы трения определяется произведением коэффициентов трения скольжения на модуль норм реакции опорной поверхности. Fтр.макс.=fN – используется лишь в том случае, если известно, что наступает предельное состояния равновесия; Во всех остальных случаях сила трения определяется из уравнения равновесия. Законы: (1)сила трения всегда направлена противоположно направленному движению тела. (2)Величина силы трения не зависит от площади соприкасающихся поверхностей. (3) Величинв силы трения зависит от состояния и материала трущихся поверхностей, а также наличия и вида смазки. (4) Предельное значение силы трения определяется по ф-ле Fтр.макс.=fN Угол трения – угол между полной реакцией опорной плоскости R и нормальной реакцией N. Геометрическое место возможных направлений предельной реакции R образует коническую поверхность – конус трения. 23) Трение качения. Трение качения При решении задач обычно силы нормальной реакции прикладывают посередине площадки по которой происходит смятие, а трение качения учитывает пары сил с моментом трения, направленным противоположно возможному движению.
Частные случаи вращения тела: 1) Равномерное вращение: =const, =t, =/t,
2) Равнопеременное
вращение: =0+t;
Скорости и
ускорения точек вращающегося тела.
28)Передаточные механизмы. Метод Виллиса. Передаточные механизмы предназначены для передачи вращения от ведущего вала к ведомому. Они реализуются в виде различного рода передач с жёсткой или гибкой связью. Фрекционные передачи функционируют за счёт сцепления между колёсами, зубчатые передают крутящий момент за счёт зацепления между зубьями. Отношение угловой скорости ведущего вала к угловой скорости ведомого называется передаточным числом i. Иногда хар-ка вращательного движения задаётся в виде числа оборотов в минуту.
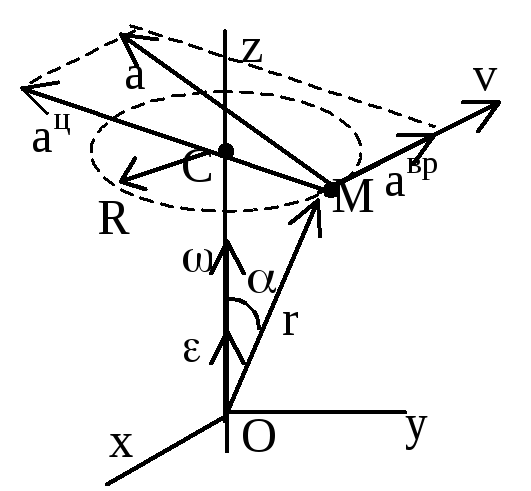
13)Выражения
скорости и ускорения точки вращающегося
тела в виде векторных произведений.
а вращ. равняется (ε x r) где r это (СМ), а центр. равняется ( x V) из этого выразим а: a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(^4+ε^2)
12)Определение
кинематических характеристик движения
точек вращающегося тела. Траектории,
закон движения. Скорость и ускорение
точек вращающегося тела. ,,ε
– основные кинематические характеристики
вращательного движения твёрдого тела.
Они одинаковы для всех точек вращательного
твёрдого тела. Скорости и ускорения
точек вращающегося тела.
a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(^4+ε^2)
15) Плоскопараллельное движение твердого тела и движение плоской фигуры. Уравнения плоского движения. Разложение плоского движения на поступательное и вращательное. Независимость вращательной части движения от выбора полюса. Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: xA= xA (t), yA= yA (t), = (t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.
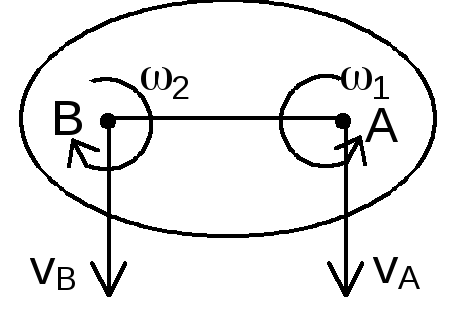
24) Сложное движение твердого тела. Сложное поступательное движение. Сложным наз такой вид движ тела при котром оно одновременно участвует в 2 или более двужениях. Рвссмотрим движ твердого тела движ относит подвиж тела со скорость V1 которое в свою очередьдвиж поступател со скоростью V2.Т.к скорость точек А и В одинаковы то результирующая при сложении движ поступательна то движ также будет поступате со скоростью равной векторной сумме относительной и посткпательной скорости.(Рис в 7.1) Vав=Vra+Vеа=V1+V2 Vав=Vrв+Vев=V1+V2 V=V1+V2 26) Сложение противоположно направленных вращений вокруг параллельных осей. В этом случаи будет поступательное движ со скоростью равной векторному произведению одного из составляющих движ на вектор соед точки проходящте через оси состав вращ (рис в 7.2) Vав=Vr+Vе ρ=OA+rB OA=ρ+rB Vr= ω2× rB Vе= ω1+ ρ Vав=ω2× rB +ω1× ρ= ω2× rB -- ω2×ρ= ω2(rB- ρ)= ω1×( ρ- rB )= ω1×OA ( везде в формуле сверху векторы)
19)Теорема Эйлера-Даламбера. Мгновенная ось вращения. Мгновенные угловая скорость и угловое ускорение тела. Скорость точек тела при сферическом движении. Формулы Эйлера. Теорема: твёрдое тело имеющее одну неподвижную точку можно переместить из одного положения в другое поворотом вокруг некоторой оси проходящей через эту точку. В соответствии с теоремой Эйлера-Даламбера вращение тел при сферическом движении происходит вокруг некоторой оси которая постоянно меняет своё положение (мгновенная ось вращения). Вектор угловой скорости ω всегда направлен вдоль мгновенной оси и в процессе движения постоянно меняет своё положение. Мгновенная
угловая скорость определяется как
производная от угловой координаты
Мгновенное угловое ускорение определяется как производная от угловой скорости по времени έ=dω/dt Скорости точек тела определяются по формулам Эйлера
x,y,z
– проекции вектора угловой скорости.
Проекция вращательной (окружной)
скорости: vx=yz
– zy;
vy=zx
– xz;
vz=xy
– yx.
Если ось вращения совпадает с осью z,
то vx=
– y;
vy=x.
Ускорение:
Вращательное
ускорение
Вектор скорости точки направлен перпендикулярно плоскости векторов ω и r таким образом чтобы смотря ему навстречу поворот на наименьший угол от ω к Vr был виден против часовой стрелки.
|
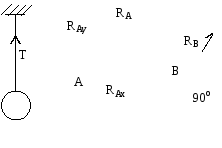
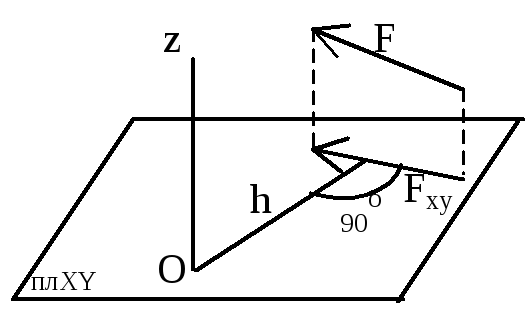
5) Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Теорема о трех непараллельных силах. Геометрическое условие равновесия: Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого. Аналитическое условие равновесия: Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0). Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0). Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат. Теорема о трех непараллельных силах: Используется когда известны величина и направление одной силы, линия действия другой и точка приложения третьей. Линии действия трех непараллельных уравновешенных сил, лежащих в одной плоскости, пересекаются в одной точке. R12=F1+F2 Равновесие равнодействующей R12 сил F1 и F2 возможно только в том случае, если третья сила F3 будет направлена по линии действия R12 противоположно ей, т.е. проходить через точку пересечения линии действия сил F1 и F2. 7) Момент силы относительно оси. Аналитическое выражение момента силы относительно оси. Момент силы относительно оси – скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси. Момент силы относительно оси равен 0 в двух случаях:
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0. 8) Связь между моментом силы относительно оси и векторным моментом силы относительно точки. Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось. 9) Сложение параллельных сил. Равнодействующая двух параллельных сил, направленных в одну сторону равна алгебраической сумме модулей составляющих сил. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Две параллельные, противоположно направленные силы, не равные по модулю, эквиваленты равнодействующей, модуль которой равен разности модулей слагаемых сил и направлены в сторону большей силы. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Если модули противоположно направленных сил равны, то такая система не имеет равнодействующей, она сообщает свободному телу вращательное движение и называется парой сил. 6) Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно точки. Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (F x r). Получаем, что векторный момент силы относительно точки – векторная величина. 10) Пара сил. Векторный момент пары сил. Алгебраический момент пары сил. Пара сил – совокупность двух противоположно направленных равных по модулю параллельных сил, действующих по несовпадающим линиям действия. Плоскость, в которой действует пара сил, называется плоскостью действия пары. Момент пары сил не зависит от выбора центра привидения, а определяется лишь модулями сил и расстоянием между л.д. – плечом пары. Векторный момент пары сил – вектор, равный векторному произведению радиус-вектора ρ, соединяющий точки приложения сил на вектор силы и направленный перпендикулярно плоскости действия пары сил таким образом, чтобы, смотря ему навстречу, пара сил стремилась поворачивать плоскость действия против часовой стрелки. Алгебраический момент пары сил равен произведению модуля одной из сил, составляющих пару, на плечо пары и имеет знак в соответствии с правилом знаков для момента силы.
25) Случаи приведения пространственной системы сил к простейшему виду. В зависимости от соотношения R0* и М0* возможны следующие случаи приведения: 1) R0*=0 и М0*=0 – система сил находится в равновесии. 2) R0*≠0 и М0*=0 – система сил приводится к равнодействующей, равной главному вектору, л.д. которой проходит через центр приведения (поступательное движение) 3) R0*=0 и М0*≠0 – система сил приводится к паре сил с моментом равным главному моменту с л.д. проходящей через центр приведения (вращательное движение) 4) R0*≠0 и М0*≠0 – система сил приводится к равнодействующей, равной главному вектору с л.д. проходящей через центр приведения (R0* перпендикулярно М0*) (плоско-параллельное движение) 5) R0*≠0 и М0*≠0 (R* параллельно М*) – система сил сводится к главному вектору и главному моменту с л.д. проходящими через центр приведения (винтовое движение) 6) R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение) 26)Приведение системы сил к динаме. Уравнение центральной оси. R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение) 31 Центры тяжести некоторых фигур. Прямоугольник – центр тяжести на пересечении диагоналей. Треугольник – центр тяжести на пересечении медиан.
Дуга окружности:
Круговой сектор
Полукруг:
Круговой сегмент: Для получения координаты необходимо разбивать сечение на круговой сектор и равнобедренный треугольник и затем применить метод отрицательных площадей. Конус, пирамида: Центр тяжести находится от основания пирамиды на расстоянии равной ¼ высоты. 30 Методы нахождения центра тяжести(симметрии, разбиения, дополнения): (1) Метод симметрии. Если объемное тело имеет плоскость или ось симметрии, то центр тяжести тела расположен на этой оси в этой плоскости. Если плоское тело имеет 2 оси симметрии то центр тяжести расположен на пересечении этих осей. (2) Метод разбиения на части. Любой тело можно разбить на части для которых известны координаты центра тяжести этих частей, а также площади массы объёмы элементов известны. Если плоское тело состоит из 3-х элементов, то центр тяжести такого тела находится в пределах треугольника, ограниченного линиями соединяющими центр тяжести элементов сечении. (3)Метод ортогональных площадей. В том случае если тело имеет вырезы, полости и т.д. необходимо применять метод разбиения на части при условии, что массы площади и объёмы свободных полостей считаются отрицательными. 29) Центр параллельных сил. Центр тяжести твёрдого тела. Центр тяжести однородного объема, площади , материальной линии. Статистический момент площади относительно оси.
Центр параллельных
сил
Центр тяжести: Центр тяжести тела – точка приложения его силы тяжести. Силы тяжести элементов тела представляют собой систему сходящихся сил, линии действия которых пересекаются в центре земли, однако угла между ними настолько малы. что ими пренебрегают, поэтому эту систему можно рассматривать как систему параллельных сил и используются те же формулы.
центр тяжести плоской фигуры (Ак – площадь)
15). Определение скоростей точек плоской фигуры. Теорема о проекциях скоростей точек плоской фигуры. Теорема: Скорость любой точки принадлежащей плоской фигуре равна геометрической сумме скорости полюса и той скорости которую имела бы точка при вращательном движении вокруг оси проходящей через полюс
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcos = vBcos. 16. Мгновенный центр скоростей. Определение скорости с помощью МЦС. Частные случаи нахождения МЦС. МЦС – точка плоскости движения плоской фигуры, скорость которой в данном положении равна 0. Скорости всех точек будут направлены перпендикулярно отрезкам соединяющим точку и МЦС в сторону угловой скорости и пропорциональны длинам этих отрезков. Частные случаи определения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. vA и vB); 3) если они при этом равны между собой, то м.ц.с. находится в , а угловая скорость =vA/=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в , и угловая скорость =vA/=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания. 17) Определение ускорений точек плоской фигуры. Мгновенный центр ускорений. Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения точки которое она имела бы при вращательном движении тела вокруг оси проходящей через полюс. aB=aA+aBA(нормальное)+aBA(тангенциальное)=aA+aBA aBA(нормальное)=ωAB^2*AB aBA(тангенциальное)=έAB*AB Существует 2 способа определения ускорений: Метод проекций Построение многоугольника ускорений
Мгновенный
центр ускорений
– точка (Q)
плоской фигуры, ускорение которой в
данный момент времени равно нулю. Для
его построения из точки А откладываем
под углом
18) Сферическое движение твёрдого тела. Углы Эйлера. Определение ускорений точек тела при сферическом движении. Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка). Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная О, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: – угол прецессии, – угол нутации, – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: =f1(t); =f2(t); =f3(t). Углы отсчитываются от осей против хода час.стр. 25) Сложение одинакого направленных вращений вокруг параллельных осей. 1)сложение одинакого направленных движений.При сложении 2 один направ движ результир яв вращ движ вокруг оси проходящей пареллельно оси вращения через точку делящую отрезок между осями относит и переносного вращения внутренним образом на части обратно пропорционально угловым скоростям составляющим вращения Vав=Vr+Vе Vав=0=Vr+Vе=> Vr= - Vе Vе=ω1*OB Vr=ω2*AB ω1*OB= ω2*AB ω1/ AB= ω2/ OB=ω/OA (рис в 7.2) 2)Сложение вращ движ направ противоположно вокруг направленных осей. При сложении 2 противоположно направленных вращений с разными угловыми скоростями результирущая яв вращ движ вокруг мгновенной оси проходящей параллельно осям состовляющим вращение через точку делящую отрезок заключенный между осями внещним образом на части обратнопропорционол угловым скоростям состав вращ Угловая скорость результирующего вращ равна разности угловых скоростей и состав вращ.( рис в 7.2) ω1≠ ω2 Vав=Vr+Vе Vе= ω1*OB Vr = ω2*AB Vе(со штрихом)= ω12 *OA ω= ω1- ω2 ω1/AB= ω2/OB=ω/OA 27) Пара вращений 3)
Пара вращений
– вращения вокруг ||-ных осей направлены
в разные стороны и угловые скорости
по модулю равны (
|
11) Эквивалентность пар. Теоремы об эквивалентности пар. Две пары сил называются эквивалентными, если они имеют геометрически равные моменты. Поэтому пара сил характеризуется при решении задач лишь моментом пары и обозначается m=M0(F1;F2). т-мы: (1)Две пары сил произвольно расположенных в пространстве эквивалентны одной паре сил с моментом, равным геометрической сумме моментов слагаемых пар. (2) еси на тело действует произвольная система пар, то ветор момента результирующей пары равен векторной сумме моментов составляющих пар. (3)Если все пары сил расположены перпендикулярно одной плоскости, то вектора моментов пар направлены перпендикулярно этой плоскости в ту или иную сторону, поэтому моменты пар можно складывать алгебраически. (4) для равновесия тела, находящегося под действием системы произвольно расположенной в пространстве пар необходимо и достаточно, чтобы момент результирующей пары был равен 0. 12) Сложение пар сил. Условие равновесия системы пар сил. Теорема о сложении пар сил: Две пары сил, произвольно расположенные в пространстве, эквивалентны одной паре с моментом равным геометрической сумме моментов слагаемых пар. Если на тело действует произвольная система (М1,М2,…,Мn) пар, то вектор момента результирующей пары равен векторной сумме моментов, составляющих пары. M=M1+M2+…+Mn=ΣMk (сверху векторы) Если две пары сил расположены в одной плоскости, то векторы моментов пар направлены перпендикулярно этой плоскости в ту или иную стороны. Поэтому моменты пар можно складывать алгебраически. M=M1+M2+…+Mn=ΣMk Условие равновесия системы пар сил: Для равновесия тела, находящегося под действием системы произвольно расположенных в пространстве пар, необходимо и достаточно, чтобы момент результирующей (эквивалентной) пары был равен 0. M=ΣMk=0 В случае, если все пары сил расположены в одной плоскости (или в параллельных плоскостях), то для равновесия необходимо равенство 0 алгебраической суммы моментов составляющих пар. 13) Основная лемма статики о параллельном переносе силы. Силу F, приложенную в точке А, можно перенести в любую другую точку плоскости ее действия параллельной линии действия, добавив при этом момент, равный моменту заданной силы F относительно нового центра приведения О. Док-во: Приложим в точку О систему двух параллельных уравновешенных сил с модулями, равными модулям заданных сил и линиям действия параллельным линиям действия заданных сил. F’=F”=F M0(F;F”)=-F·h=M0(F’) Полученная пара сил и сила F' эквивалентны заданной силе F. F~(M0(F1;F”),F’) 14) Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил. Любую систему произвольно расположенных в пространстве сил можно привести к одной силе, равной геометрической сумме составляющих сил и одной паре сил с моментом, вектор которого равен геометрической сумме векторов моментов составляющих сил относительно нового центра приведения. Главный вектор R это равнодействующая некоторой системы сходящихся сил (F1'_F2'….Fn'). А главный момент Mo это результирующий момент некоторой системы пар сил (Mo(F1)_Mo(F2…..Mo(Fn). 15) Перемена центра приведения пространственной системы сил. Инварианты приведения пространственной системы сил. Инварианты статики – это величины, значение которых не зависит от выбора центра привидения. Вектор главного момента относительно нового центра привидения равен сумме двух векторов: главного момента относительно старого центра привидения и момента главного вектора относительно нового центра привидения. R=сумма (Fk) он является первым инвариантом (векторным) т.к при его параллельном переносе в новый центр привидения, его модуль и направление не меняется. Mo1*R=Mo2*R=const – второй инвариант (скалярный) произвольной системы сил. 16) Уравнения равновесия плоской системы сил. Частные случаи. Для того, чтобы плоская система сил находилась в равновесии, необходимо выполнение 2 условий: 1.Моменты сил относительно осей расположенных в плоскости должны быть равны 0 2.Проекции сил на оси, произвольно выбранной системы координат должны быть равны 0 Система уравнений равновесия произвольной плоской системы сил: Fkx=0; Fky=0; Mо(Fk)=0 Частные случаи: 1. Mа(Fk)=0; Mв(Fk)=0; Mс(Fk)=0. Эту систему уравнений нельзя использовать если точки А, В, С лежат на одной прямой 2. Fky=0; Mа(Fk)=0; Mв(Fk)=0; Эту систему уравнений нельзя использовать, если ось ОУ перпендикулярна отрезку АВ. 17) Уравнения равновесия плоской системы параллельных сил.Для системы параллельных сил на плоскости имеем 2 условия равновесия: М*=0 R*=0 Для получения уравнений равновесия одну из осей координат надо направить параллельно заданным силам ( например ось ОУ). Тогда все силы проектируются на ось ОУ, а проекция каждой силы на ось ОХ равна нулю. Этих два условия равновесия системы параллельных сил на плоскости можно выразить в виде двух уравнений: Fkу=0; Mо(Fk)=0; Эти уравнения называют основными уравнениями равновесия параллельных сил на плоскости. Центр моментов для этой системы уравнений можно выбирать произвольно. Существует и другая система двух уравнений равновесия параллельных сил: MА(Fk)=0; MВ(Fk)=0; При этом прямая АВ не должна быть параллельна заданным силам. 1.Предмет кинематики. Пространство и время в класической механике.Относительность движения. Траектория движения точки. Основная задача кинематики. Кинематика – раздел теоретической механики изучающий законы механического движения материальных точек или тел без учёта причин, вызывающих это движение. Механическое движение – изменение положения тела в пространстве с течением времени. Любое движение точки или тела рассматривается относительно какой-либо системы отсчёта. Обычно систему отсчёта связывают с землёй, считая её неподвижной. Если рассматривать движение тела относительно подвижной системы отсчёта, то при расчётах необходимо учитывать движение подвижной системы отсчёта относительно неподвижной. Траектория точки – геометрическое место последовательных положений точки в процессе её движения. Прямолинейное, если траектория-прямая, в других случаях криволинейное.Основные задачи кинематики: - определение закона движения точки или тела в выбранной системе отсчёта. - По заданному закону определить кинематические характеристики движения. 2)Способы задания движения точки (векторный, координатный, естественный). Движение точки считается заданным, если существует зависимость, позволяющая определить положение точки в пространстве в произвольный момент времени, эта зависимость называется законом движения. Способы задания движения: (1) Естественный – используется. Если известна траектория движения, уравнение движения точки по этой траектории, начало отсчёта и положительное направлении движения. S=S(t) – угловая координата. (2) Векторный – положение описывается радиус-вектором проведённым из некоторой неподвижной точки. r=r(t) уравнение движения при векторном способе. Траектори в данном случае является гадографом радиус-вектора. (3) координатный – положение точки задаётся зависящими от времени дифференцируемыми функциями координат. X=x(t) y=y(t) z=z(t). y=f(x) – уравнение траектории. 3)Скорость точки при векторном способе задания движения. Величина равная отношению приращения дэльта(r) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средней скоростью точки за это время Vср.= дэльта(r)/дэльта(t). При дэльта(t) стремящимся к 0: V= dr/dt скорость точки в данный момент времени. Скорость всегда направлена по касательной к траектории движения. 4) Ускорение точки при векторном способе задания движения. Величина равная отношению приращения дэльта(V) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средним ускорением точки за это время a cр.= дэльта(V)/дэльта(t). При дэльта(t) стремящимся к 0: a= dV/dt ускорение точки в данный момент времени. Ускорение всегда направлена по касательной к гадографу вектора скорости. 5) Скорость и ускорение точки при координатном способе задания движения. V= dr/dt = d(xi+yj+zk)/dt = Vxi + Vyj + Vzk где Vx=dx/dt, Vy=dy/dt, Vz=dz/dt – проекции вектора скорости на оси координат V=корень(Vx^2+Vy^2+Vz^2)Положени вектора Vопределяется направлением косинусов , а именно углов между направлением вектора V и положительно направленной соответствующей оси координат. 6) Скорость точки при естественном способе задания движения. V= dS/dt*dr/dS сдесь dS/dt – v – алгебраическая скорость точки, а dr/ds – ŧ(тау) – вектор, направленный по направлению вектора dr. V= ŧ(тау)*v. 7) Естественный трехгранник. Разложение ускорения по естественным осям. Касательное и нормальное ускорения. Если выбрать в качестве осей координат независимые оси ŧ(тау), n, в - которые связаны с движущейся точкой при этом ŧ(тау)-является касательной, n – нормалью , в – бинормалью, тогда ŧ(тау) и n образуют касательную плоскость, n и в нормальную плоскость, в и ŧ(тау) – спрямляющуюся плоскость, это и есть естественный трёхгранник. Нормальное ускорение точки всегда направлено к центру кривизны траектории(a норм. =V^2/q, где q – радиус кривизны траектории), а касательное по касательной к траектории, если знаки касательного ускорения и скорости совпадают, то и направления их тоже совпадают, или наоборот(а ŧ(тау)=dV/dt) 8) Частные случаи движения точки. Смысл касательного и нормального ускорений. Касательное ускорение показывает изменение скорости по величине, нормально – по направлению. Если (а ŧ(тау)=0) и ( a норм.=0) – движение равномерное и прямолинейное, если (а ŧ(тау)=0) и ( a норм. не равно 0) то криволинейное и равномерное, если (а ŧ(тау)не равно 0) и ( a норм.=0) то прямолинейное равномерное, если (а ŧ(тау) не равно 0) и ( a норм. не равно 0) то криволинейное неравномерное. При постоянном а ŧ(тау) движение либо равноускоренное, либо равнозамедленное. 9) Поступательное движение твердого тела. Теорема о траекториях,скоростях и ускорениях точек тела при поступательном движении.Поступательным называется такое движение, при котором в теле можно выделить прямую, остающуюся параллельной самой себе в процессе движения. Т-ма: Все точки тела, движущиеся поступательно имеют в данный момент геометрически равные скорости и ускорения и движутся по одинаковым траекториям. Для изучения тела, движущегося поступательно достаточно изучить движение одной его точки, обычно рассматривают центр тяжести.
10)Вращательное
движение твердого тела вокруг
неподвижной оси. Уравнение вращательного
движения тела. Угловая скорость и
угловое ускорение. Векторы угловой
скорости и углового ускорения.
Вращательное
движение
тела –
такое движение твердого тела, при
котором точки, принадлежащие некоторой
прямой, остаются неподвижными, а
остальные точки описывают окружности
в плоскости перпендикулярно оси
вращения. Уравнение (закон) вращательного
движения: =f(t)
– угол поворота тела в радианах.
Угловая
ск-сть:
Вектор угловой
скорости тела, совершающего вращение
вокруг неподвижной оси, направлен
вдоль оси вращения так, что если
смотреть ему навстречу вращение будет
против час. стрелке. Угловое ускорение
тела:
20) Общий случай движения свободного твёрдого тела. Уравнения движения свободного твёрдого тела. Скорости точек тела. Движение
свободного тв.тела
(общий
случай движения). Свободное тв.тело
имеет шесть степеней свободы. При
рассмотрении движения св.тв.тела,
кроме неподвижной системы координат
Oxyz,
вводится подвижная система координат
Ax1y1z1,
которая связана с телом в точке А.
Тогда движ. св.тв.тела представляет
собой сложное движение, которое можно
рассматривать как состоящее из
поступательного движения вместе с
полюсом (А) и сферич. движ. вокруг
полюса. Ур-ия движ.св.тв.тела: xA=f1(t);
yA=f2(t);
zA=f3(t);
=f4(t);
=f5(t);
=f6(t)
(углы Эйлера). Первые три ур-ия определяют
поступательную часть движ. и зависят
от выбора полюса, остальные три
определяют сферич. движ. вокруг полюса
и от выбора полюса не зависят. Скорость
любой точки св.тв.тела = геометрической
сумме скорости полюса и скорости этой
точки в ее сферическом движении вокруг
полюса.
21) Сложное движение точки. Абсолютное, относительное и переносное движения. Абсолютные, относительные и переносные скорость и ускорение точки. Основное векторное уравнение кинематики сложного движения. Сложным называется такое движение тела при котором оно одновременно участвует в двух или нескольких движениях. В рассмотрение вводится подвижная и неподвижная система отсчёта аналогично сложному движению тела. Сложное движение тела рассматривается как совокупность двух движений – относительного и переносного.В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O1x1y1z1). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона). 22) Теорема сложения скоростей при сложном движении точки Скорость точки относит НСО наз. абсолютной Vабс (Va).Скорость точки относит ПСО наз. относительной Vотс (Vr).Скорость которую имела бы точка находясь в данном положении движущегося тела при отсутствии относит. Движ. Наз. переносная скорость движ. Vпер (Vc). Теор. абсолют скорость точки равна геометр. Сумме относит. и перенос. Скорости Va=Vr+Vc. Док. Пусть точка М приходит в полож М3 двигаясь по троектории обсолютного движения.(Рис в 4.1).Для определения Vr необход мысленно остановить переносное движ. Для опред Ve необход мысленно остановить относительное движ. Поэтому для опред. абсолют. Скорости точ. Необход снач. Опред. Полож. Точ. В требуемый момент времени на троектории относит движ. 23) Теорема сложения ускорений при сложном движении точки. Ускорение Кориолиса. Определение направления ускорения Кориолиса. Правило Жуковского. Смысл ускорения Кориолиса. 1) Переносное движение поступательно. Абсолютное ускорение точки равна геометрич. Сумме относит и переносного движ aa=ar+ae . Если относит движение движ по криволинейной троектории то aa= arn + ar t+ae.Для определения относит ускорения нужно остановить переносное движение. Для определения переносного ускорения нужно остановить относительное движение. 2)Обсолютное ускорение точки при не поступательном переносном движении равна геометрич сумме aa=ar+ae+ aс Кариолисово ускорение характер:1)Изменение велечины переносной скорости в следствии относит движения.2)Изменением направления вектора относит скорости в след непоступательного переносного движ. . aс =2 aсώe Vrsin(ώr,Vr) Кариолисово ускорение опред по правилу векторного произведения. . aс┴ (ώe, Vr) и направлено таким образом чтоб смотря ему навстречу поворот от ώe к Vr на найменьший угол происходит против часовой стрелки.
|

 1)
Предмет статики. Основные понятия и
определения
1)
Предмет статики. Основные понятия и
определения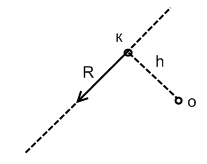

 11)Частные
случаи вращательного движения.
11)Частные
случаи вращательного движения.
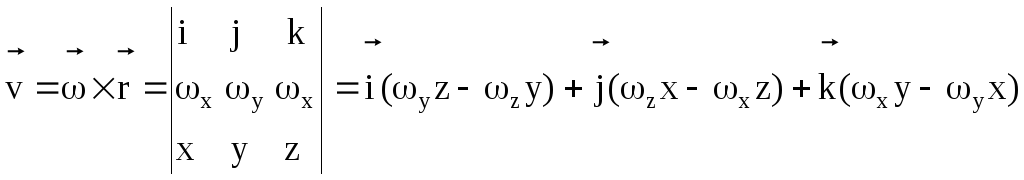
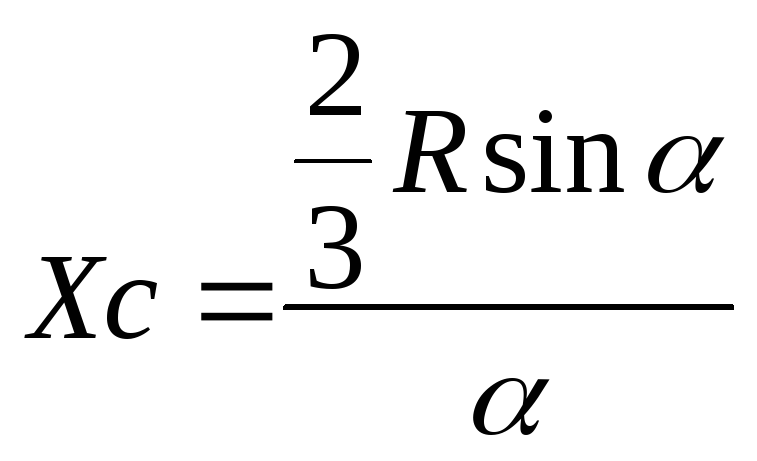 Ус = 0
Ус = 0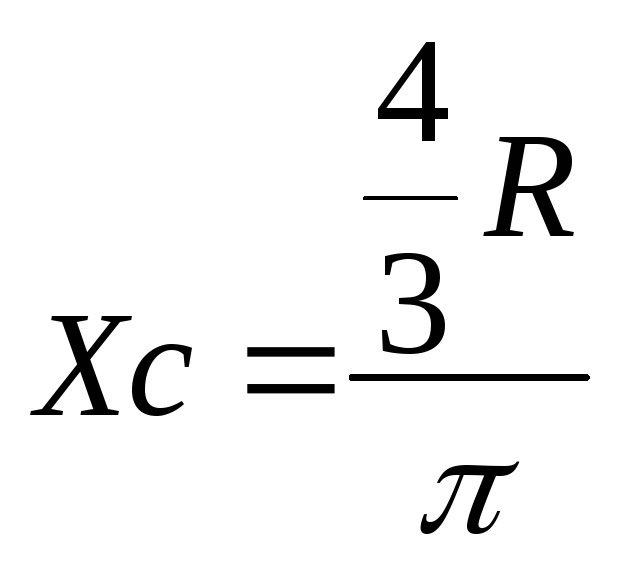 Ус = 0
Ус = 0