для первого курса / для первого курса / ВЫШКА / 20. Кривые 2 порядка

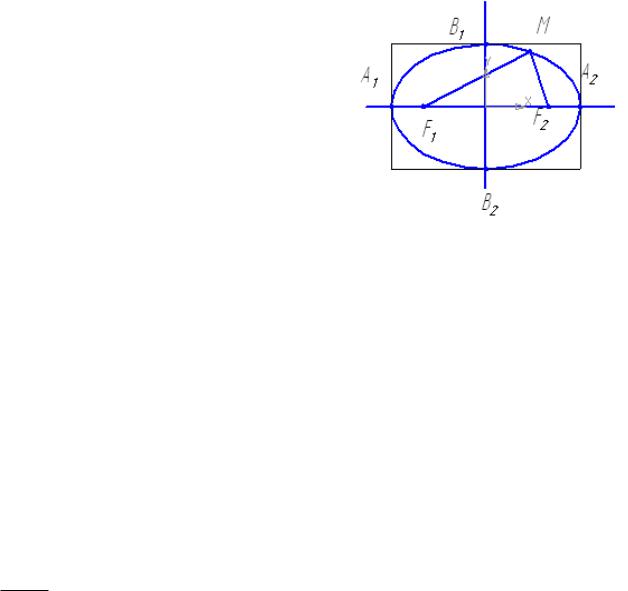
КРИВЫЕ ВТОРОГО ПОРЯДКА

ОПРЕДЕЛЕНИЕ 12. Кривой второго порядка называется множество точек плоскости, декартовы координаты X и Y которых удовлетворяют алгебраическому уравнению второй степени:

Ax2 2Bxy Cy 2 Dx Ey F 0 ,

(40)

где A , B , C , D , E , F – постоянные действительные числа. Уравнение (40) называется общим уравнением кривой второго порядка.

Причем первые 3 слагаемых образуют квадратичную форму. С помощью поворота координатных осей это уравнение можно привести виду, не содержащему слагаемого с произведением переменных , Поэтому изучаем уравнение

Ax2 Cy2 Dx Ey F 0

Путем выделения полного квадрата для х и у мы получаем каноническое уравнение 2-го порядка. При этом возможны следующий случаи.

1.Если А *С больше 0, следовательно будет эллипс

	x 2			y 2		1
	a	2		b	2
						Где точки А1(-а,0)

А2(а,0) В1(0,b) В2(0,-b) в данном случае центр системы является центром симметрии эллипса…, а оси осями симметрии. Элипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух значений точек F1 и F2(фокусов есть величина постоянная.

F1M+F2M = 2a

F1(-c;0) F2(c;0) F1F2=2c

Поскольку а с, то а2=b2+с2. Величина Е=с/а называется эесцентриситот эллипса и характеризуется его выпуклостью, для эллипса он меньше единицы. Если фокусы эллипса лежат на ОУ, то коническое уравнение эллипса примет вид.

x 2	y 2 1 и такой эллипс вертикальный.				Если			полуоси эллипса равны
b2	a2
а=b=R, то мы получаем уравнение окружности. x 2					y 2			R2 . Еокр=0
Если центр находиться не в начале координат , а смещена в некоторую точку
1.уравнение эллипса имеет вид:		x x0 2		y y0	2	1
		a2		b2
2. уравнение окружности имеет вид x x 2 y y						0	2	R2
			0

2. А*С меньше 0 – гипербола

x 2 y 2 1

a2 b2

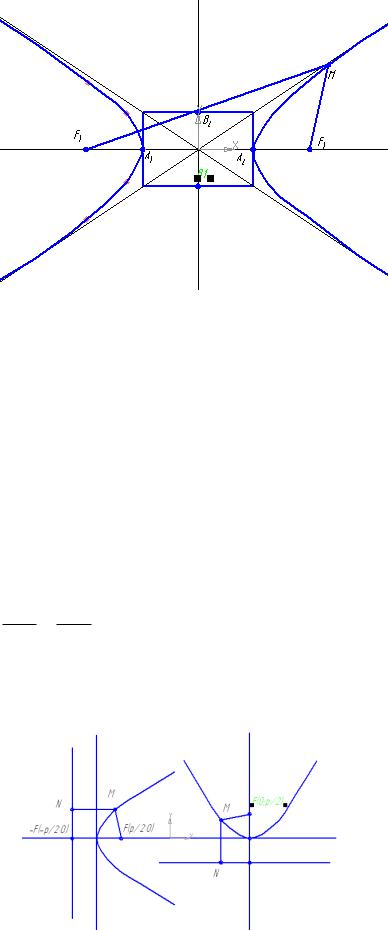
Асимптоты гиперболы в общем случае: y=(+-)bx/a- асимптотами называются прямые линии, к которым приближаются заданные кривые на бесконечном удалении.

А1(-а,0) А2(а,0) – вершины гиперболы длинна а действительная полуось гиперболы. В1(0,b) В2(0,-b) мнимые вершины гиперболы b-мнимаю полуось гиперболы. Уравнение асимптоты из уравнения прямой линии^

y=kx+b, b=0 k=tg =-y/x

Гиперболой называется геометрическое место точек плоскости, абсолютное значение разности расстояний которых до двух точек F1 и F2(фокусов) есть величина постоянная и равная

F1M-F2M = 2a F1F2=2c

Прямоугольник с центром в начале координат и со сторонами параллельными осям и проходящим через вершины гиперболы называется основным прямоугольником гиперболы. с а а2+b2=с2

Е=с/а больше единицы, и характеризует выпуклость основного прямоугольника гиперболы. Если полуоси гиперболы равны, то гипербола называеться равносторонней, основной прямоугольник гиперболы превращается в квадрат и Е= 1.4и уравнение гиперболы приобретает вид: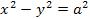 Если равностороннюю гиперболу повернуть на 45 градусов против часовой

стрелки относительно начала координат то получим школьную кривую.

Если фокусы гиперболы расположены на оси ОУ то ее уравнение принимает вид:

x 2 y 2 1 х=(+-)ау/b

a2 b2

3. A*C=0 Произведение равняется 0 если один из множителей равняется 0 Первый вариант. А=0 С не равняется 0. И у2=2рх. Если взять произвольную точку на параболе М то расстояние MN=FM/

Второй вариант С=0 А не равно 0 x2=2ру.

Парабола - геометрическое место точек плоскости, равноудаленных от фиксированной точки F и от фиксированной прямой, не проходящей через эту

точку(директриса) Число р называется параметром параболы и представляет собой расстояние от фокуса до директрисы Е=1