для первого курса / для первого курса / тер мех / 22. Свободные колебания. Затухающие колебания

Свободных колебаний точки без учета сил сопротивления. Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы F, направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы F

на ось Ох (рис. 253) будет

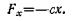(65)

Сила F, как видим, стремится вернуть точку в равновесное положение О, где F=0; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости или сила притяжения.

Найдем закон движения точки М. Составляя дифференциальное уравнение движения в проекции на ось х, получим:

Деля обе части равенства на т и вводя обозначение

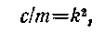(66)

приведем уравнение к виду

(67)

Уравнение (67) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного

однородного дифференциального уравнения второго порядка ищут в виде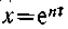

.Полагая в уравнении (67) 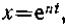, получим для определения n

характеристическое уравнение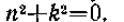 Поскольку корни этого уравнения являются чисто мнимыми, то, как известно из теории дифференциальных уравнений, общее решение уравнения (67) имеет вид

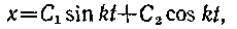(68)

где C1 и С2 — постоянные интегрирования. Если вместо постоянных С1 и С2 ввести постоянные A и α такие, что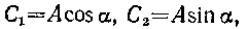 то получим

или

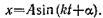(69)

Это другой вид решения уравнения (67), в котором постоянными интегрирования являются А и α. Им удобнее пользоваться для общих исследований.

Скорость точки в рассматриваемом движении

(70)

Промежуток времени Т , в течение которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза

изменяется на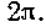Следовательно, должно быть 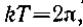откуда период

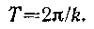(71)

Величина ν, обратная периоду и определяющая число колебаний, совершаемых за 1 с, называется частотой колебаний:

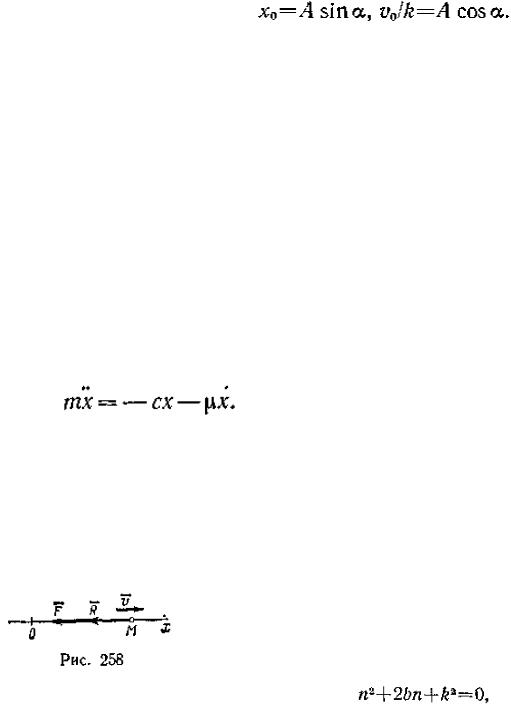
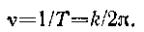(72)

Отсюда видно, что величина k отличается от ν только постоянным множителем 2π. В дальнейшем мы обычно для краткости частотой колебаний будем называть и величину k.

Найдем теперь значения постоянных интегрирования А и α.

Определение А и α. по начальным условиям. Считая, как всегда, при t=0 х=х0 и vx=v0, получим из:

Отсюда, складывая сначала почленно квадраты этих равенств, а затем деля их почленно одно на другое, найдем:

(73)

Свойства свободных колебаний. В заключение отметим следующие важные свойства свободных колебаний: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следовательно, и период Т колебаний от начальных условий не зависят определяются равенствами (66) и (71) и являются неизменными характеристиками данной колеблющейся системы.

Рассмотрим, как влияет на свободные колебания сопротивление, создаваемое силой вязкого трения т. е. силой, пропорциональной первой степени

скорости: 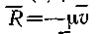(знак минус указывает, что сила R направлена противоположно V. Пусть на точку при ее движении действуют восстанавливающаяся сила F и сила сопротивления R (рис. 258). Тогда

и дифференциальное уравнение движения будет

Деля обе части уравнения разделим на m, получим

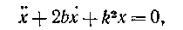(76)

где обозначено

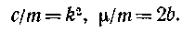(77)

Легко проверить, что величины k и b имеют одинаковые размерности (1/время), это позволяет сравнивать их с друг с другом.

Уравнение (76) представляет собой дифференциальное уравнение свободных колебаний при сопротивлении, пропорциональном скорости. Его решение, как и решение уравнения (67), ищут в виде

Подставляя это значение х в уравнение (76),

получим характеристическое уравнение

корни которого будут

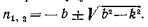(78)

1. Рассмотрим случай, когда k>b, т. е. когда сопротивление по сравнению с восстанавливающей силой мало. Введя обозначение

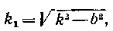(79)

получим из (78), что 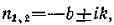т. е. что корни характеристического уравнения являются комплексными. Тогда общее решение уравнения (76) будет,

очевидно, отличаться от решения уравнения (67) только множителемт. е.

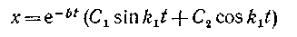(80)

или, по аналогии с равенством (69),

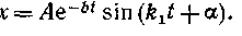(81)

Входящие в (81) величины Л и а являются постоянными интегрирования и определяются по начальным условиям.

Колебания, происходящие по закону (81), называются затухающими, так как

благодаря наличию множителя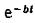величина х=0М (рис. 258) с течением времени убывает, стремясь к нулю. График этих колебаний показан на рис. 259 (график заключен между пунктирными кривыми

так как sin(k1t+a) по модулю не может стать больше единицы).

Промежуток времени Т и равный периоду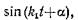т. е. величину

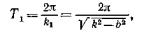(82) принято называть периодом затухающих колебаний.

2.Рассмотрим теперь случай, когда b>k, т. е. когда сопротивление по

сравнению с восстанавливающей силой велико. Вводя обозначение 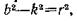найдем, что в этом случае корпи характеристического уравнения (78) равны т. е. оба действительны и отрицательны. Следовательно, решение уравнения (76), описывающее закон движения точки, имеет при b>k вид

3. В заключение рассмотрим случай, когда b=k. Корни характеристического уравнения (78) будут при этом тоже действительны ми, но

кратными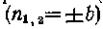и общее решение уравнения (76) примет вид (что можно

проверить 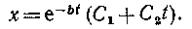подстановкой х в уравнение.

Движение точки в данном случае тоже не будет колебательным и она со временем стремится асимптотически к равновесному положению x—Q [по правилу Лопиталя График движения в зависимости от

начальных 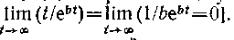условий имеет тоже вид кривых, показанных на рис. 260.