Курсовая работа / Вариант 18 - Браженков - 2004 / Курсовик по стандартизации (18вар)

Российский химико-технологический университет им. Д.И. Менделеева.

кафедра стандартизации и сертификации

Курсовая работа.

На тему: “Методы обработки экспериментальных данных, оценка распределений и их параметров, проверка гипотез о распределениях ”

Выполнил:

студент гр. Н-51

Скирда А.А.^®

Вариант - 18

Проверил:

Браженков А.И.

Москва 2004 г.

4,2	5,4	8,4	12,6	4,8	0,6	13,8	1,2	9,6	32,4
33	3,6	24,6	27,6	4,2	40,8	30	15	1,2	3
56,4	6	0	14,4	4,2	0	37,2	7,2	27	6,6
14,4	0	13,2	7,2	6	13,8	0	17,4	3	1,8
20,4	10,8	38,4	32,4	0,6	15	22,8	17,4	21	7,8
16,2	3,6	3	12,6	4,2	13,8	55,2	25,2	1,8	0
11,4	2,4	3	5,4	6,6	0,6	9,6	9,6	3,6	49,2
45	5,4	5,4	12	5,4	0,6	42	4,2	15,6	0,6
12	0	4,2	6,6	0	20,4	25,8	28,8	18,6	6,6
6,6	12,6	4,2	1,2	5,4	34,8	31,8	4,2	11,4	30,6

Получено сто значений одной и той же величины Х:

Решение.

1. По формулам находим точечные оценки математического ожидания и дисперсии случайной величины Х (n=100)

Математическое ожидание: МХ == = 13,4

Исправленная дисперсия: X = = 179,6

Выборочная дисперсия: X = X = 177,8

2. Рассчитаем доверительные интервалы для математического ожидания и дисперсии, предварительно задав доверительную вероятность (1 - ) = 0,95. Тогда по таблице значений функции Лапласа находим и, следовательно, искомые доверительные интервалы будут иметь вид:

• для математического ожидания:

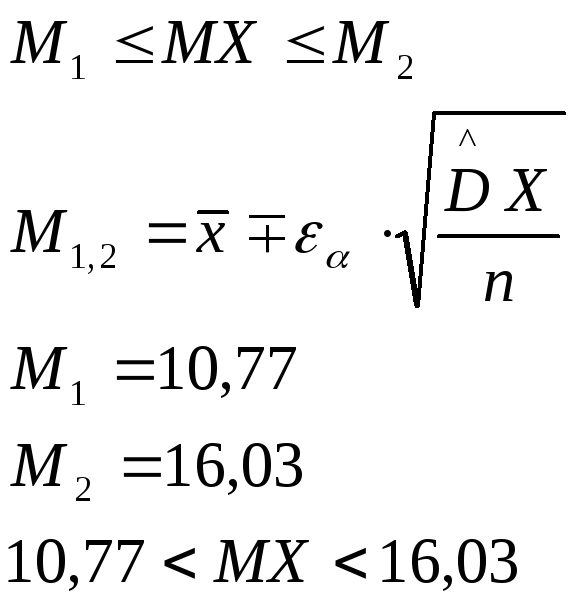
• для дисперсии:

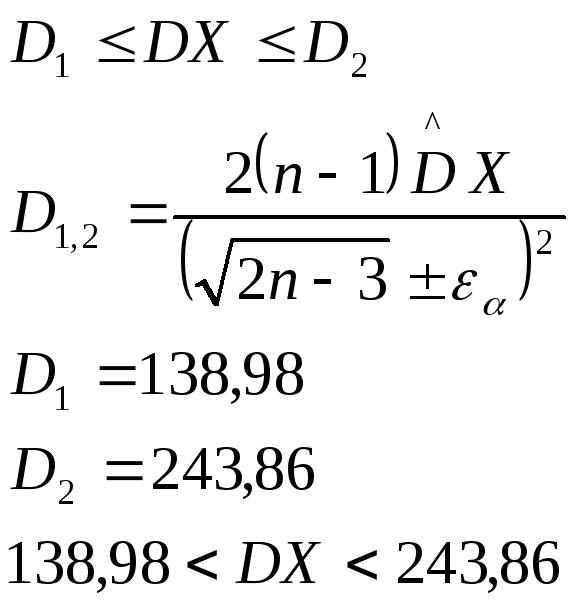
3. Находим точечную оценку вероятности попадания случайной величины X в интервал (0,7;1) = (9,4;13,4).Так как в этот интервал попало m=12 экспериментальных значений, то искомая оценка будет равна:

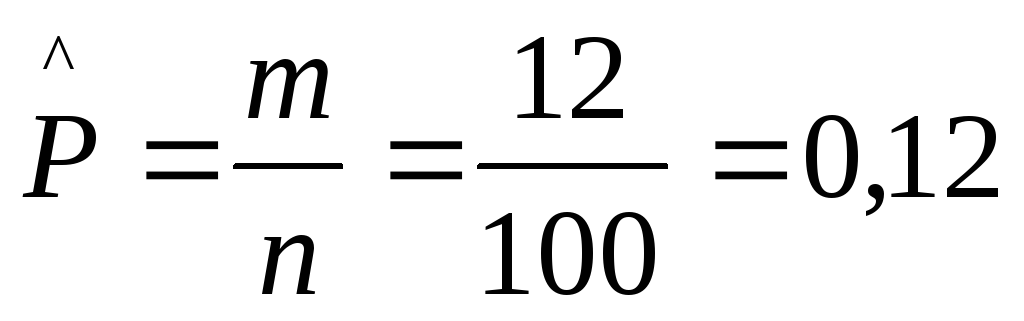
4. Рассчитываем доверительный интервал для вероятности Р, оцененной в предыдущем пункте. Доверительная вероятность равна (1-) = 0,9. Тогда =1,65 , и искомый интервал имеет вид :

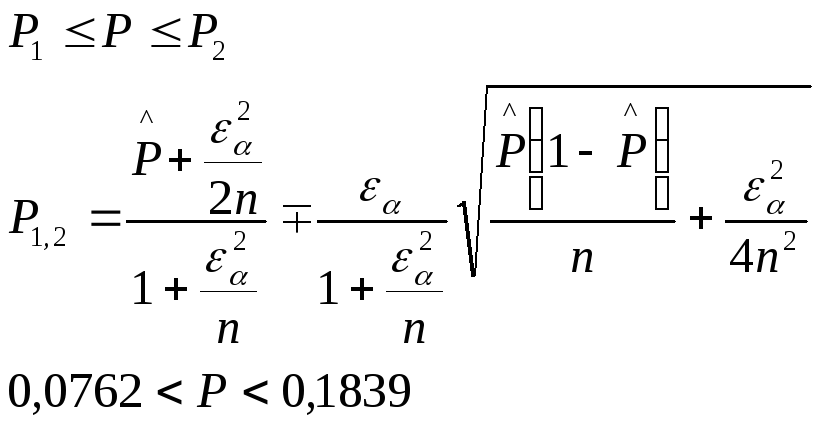
5. Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (0;60) и разбиваем его на 10 равных разрядов, каждый длиной 6. Для каждого разряда рассчитываем:

• значение гистограммы Г(x):

, где - число экспериментальных точек, попавших в этот разряд , а - его длина.

• частоты попадания экспериментальных точек в разряды гистограммы:

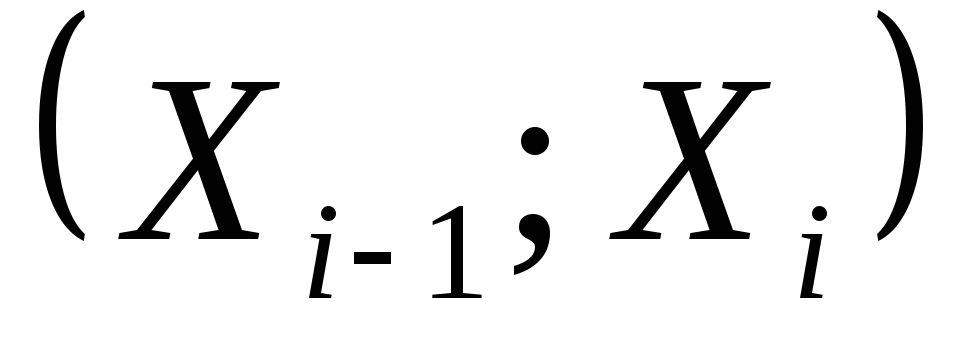
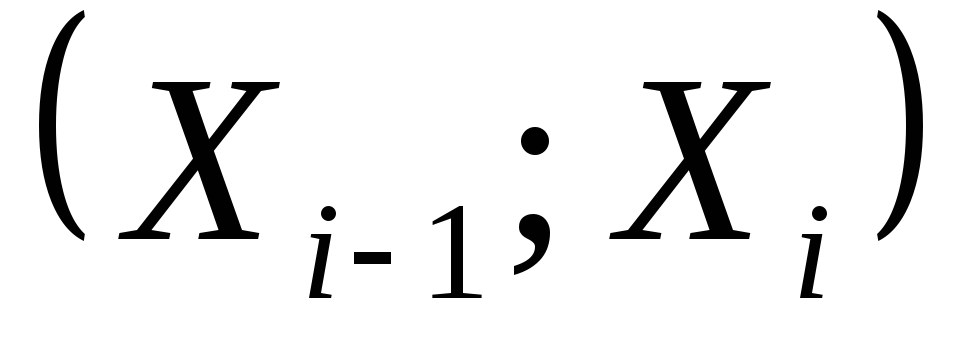
Разряд	Частота попадания Х в разряд	Значение гистограммы Г(x)
(0;6)	0,42	0,0700
(6;12)	0,17	0,0283
(12;18)	0,15	0,0250
(18;24)	0,05	0,0083
(24;30)	0,07	0,0117
(30;36)	0,06	0,0100
(36;42)	0,04	0,0067
(42;48)	0,01	0,0017
(48;54)	0,01	0,0017
(54;60)	0,02	0,0033

Соответствующую эмпирическую функцию рассчитываем по формуле:

;

где - число экспериментальных точек, лежащих левее х.

6. Находим доверительные области для плотности распределения f(x) и функции распределения F(x).

а) Для плотности распределения.

На каждом разряде находим доверительную область для вероятности попадания исходной величины X в этот разряд. Вычисляем по формуле (пункт 4.) с заменой величины 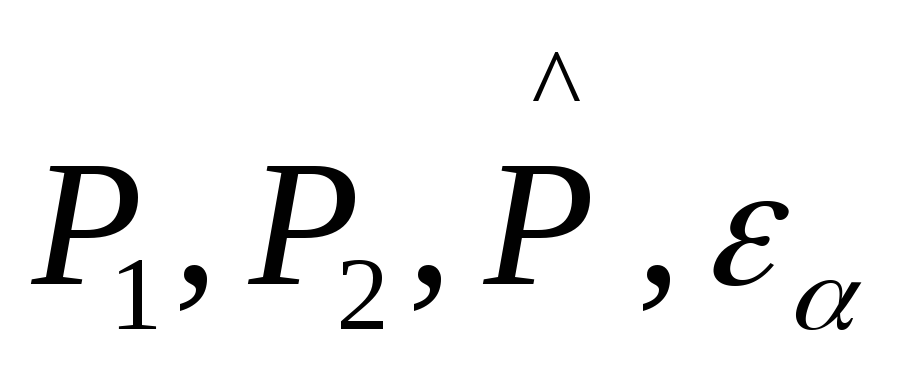соответственно на 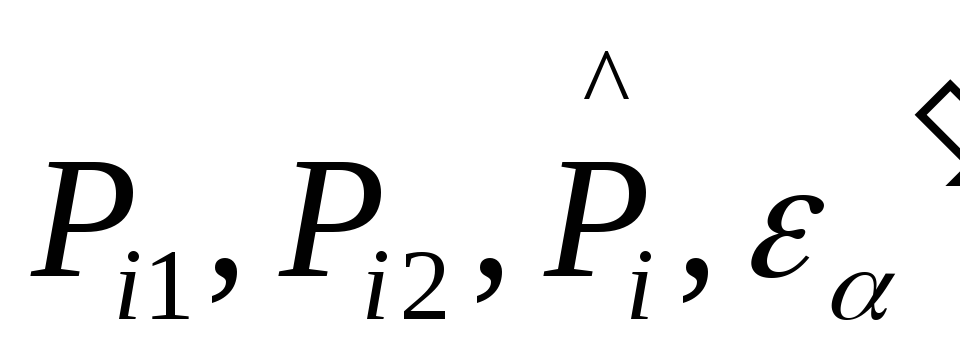. В данном случае общее число разрядов r=10 плюс 1 полубесконечный разряд, r=11. Доверительная вероятность (1-)=0,95 , из условия:

= 0,4977 и, используя таблицу значений функции Лапласа, находим = 2,84.

- плотность на i-ом разряде;

- доверительные границы для плотности , которая находится по формуле:

, ; длина разряда.

б) Для функции распределения.

По таблице распределения величины (распределение Колмогорова) находим ее величину, соответствующую коэффициенту доверия (1-) = 0,8. Она равна =1,07. Затем рассчитываем доверительную область для функции распределения F(x):

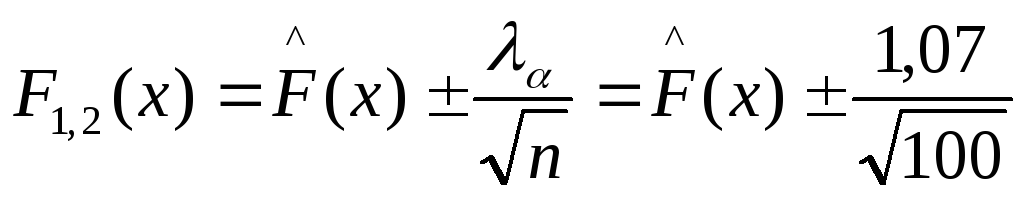= 0,107

7. Из формы гистограммы следует, что гипотетическим распределением может быть экспоненциальное распределение

для плотности распределения:

для функции распределения:

8. Проверка правдоподобия гипотезы о совпадении выбранного закона распределения с истинным законом при заданном уровне значимости.

а) С помощью критерия Колмогорова.

Максимальное различие между гипотетической и эмпирической функциями распределения равно в данном случае:

Экспериментальное значение критерия Колмогорова равно:

Гипотетическое значение этого критерия при уровне значимости α=0,1 (по таблице Колмогорова) равно 1,22

Таким образом, , следовательно, гипотеза по критерию Колмогорова является правдоподобной.

б) С помощью критерия согласия

Экспериментальное значение вычисляется по формуле:

где для экспоненциального распределения определяется следующим образом:

;

0,42	0,361
0,17	0,230
0,15	0,147
0,05	0,094
0,07	0,060
0,06	0,038
0,04	0,025
0,01	0,016
0,01	0,010
0,02	0,006

Экспериментальное значение,согласно вышеуказанной формуле = 10,05.

Теоретическое значение зависит от двух величин (α,s). Уровень значимости α = 0,1; число степеней свободы:

S = r – 1 – k

Для экспоненциального распределения k = 1

S = 11-1-1 = 9

Значит, теоретическое значение (по табл.)

Таким образом,

<;

гипотеза является правдоподобной.