
Курсовая работа / Вариант 22 - 2006 / Stand 22
.docРОССИЙСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
ИМ. Д. И. МЕНДЕЛЕЕВА
Курсовая работа по стандартизации.
Вариант №22.
Студент:
Группа:
Преподаватель: Горбунов И.А.
Москва 2006
Задание:
Производится исследование точности измерения приборов на химическом производстве. Зарегистрированы следующие ошибки показаний прибора:
|
-26 |
68 |
200 |
-56 |
7 |
-147 |
220 |
13 |
-225 |
25 |
|
14 |
157 |
136 |
-17 |
272 |
170 |
-98 |
185 |
73 |
-115 |
|
-128 |
121 |
-63,8 |
53,3 |
55 |
-39 |
134 |
54 |
83 |
111 |
|
-82 |
20 |
41,9 |
-9 |
67 |
109 |
-15 |
72 |
-107 |
19 |
|
-119 |
-119 |
159 |
-100 |
75 |
136 |
43 |
-279 |
16 |
111 |
|
-70 |
198 |
-179 |
113 |
71 |
46 |
0 |
-107 |
72 |
-103 |
|
97 |
30 |
-139 |
307 |
125 |
55 |
-7 |
34 |
20 |
158 |
|
170 |
153 |
-207 |
-141 |
68 |
-162 |
-40 |
108 |
36 |
115 |
|
89 |
-84 |
16 |
154 |
-55 |
-33 |
50 |
1 |
181 |
-53 |
|
-117 |
-7 |
133 |
-105 |
2 |
225 |
229 |
-17 |
-17 |
-51 |
Найти:
-
Используя табличные значения необходимо найти математическое ожидание и дисперсию (Мх, Dx)
-
Найти доверительный интервал для Мх, Dx, соответствующий доверительной вероятности (1-α) = 0,85.
-
Оценить вероятность попадания случайной величины Х в интервал
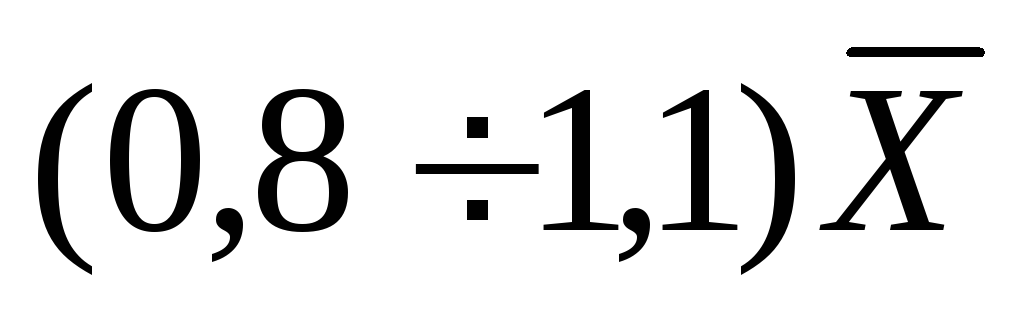
Решение:
-
Найти оценки математического ожидания и дисперсии случайной величины Х:
n = 100
Оценка математического ожидания:
![]()
Оценка дисперсии:
![]()
![]()
-
Найти доверительный интервал для Мх, Dx, соответствующий доверительной вероятности (1-α) = 0,85:
Доверительная вероятность
![]() ,
по таблице значений функции Лапласа
находим
,
по таблице значений функции Лапласа
находим
![]() 1,44
1,44
![]()
9,808 < MX < 42,940
![]()
10935,959 < DX < 16506,602
-
Оценить вероятность попадания случайной величины Х в интервал
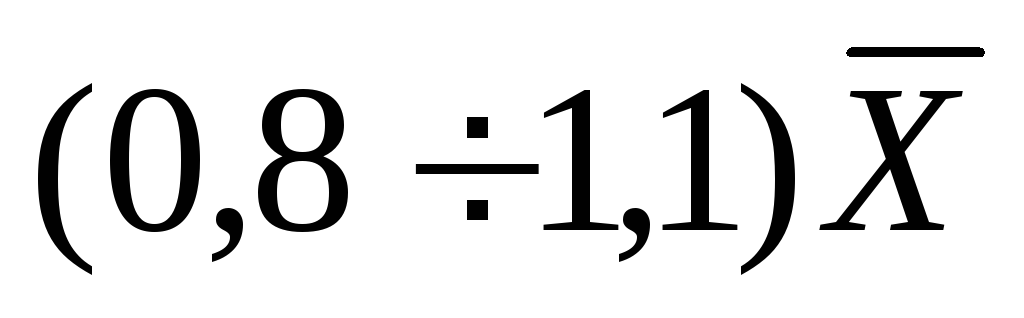
В интервал
![]() попало
m=1
значение.
попало
m=1
значение.
![]()
-
Рассчитываем доверительный интервал для вероятности
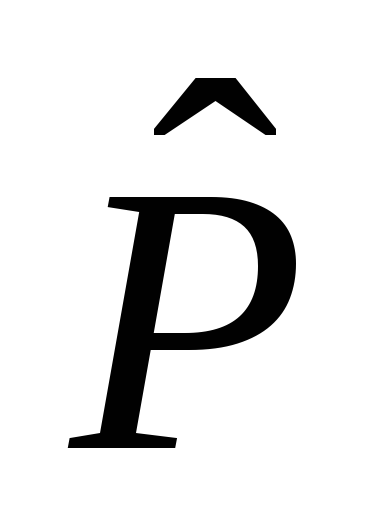 ,
при условии равенства коэффициента
доверия
,
при условии равенства коэффициента
доверия
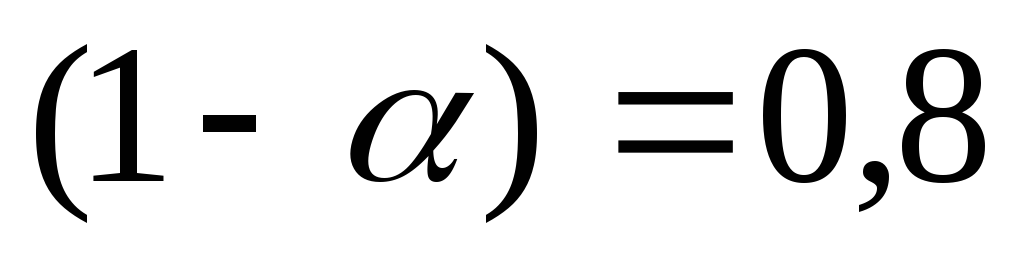
Доверительная вероятность
![]() ,
по таблице значений функции Лапласа
находим
,
по таблице значений функции Лапласа
находим
![]() 1,29
1,29
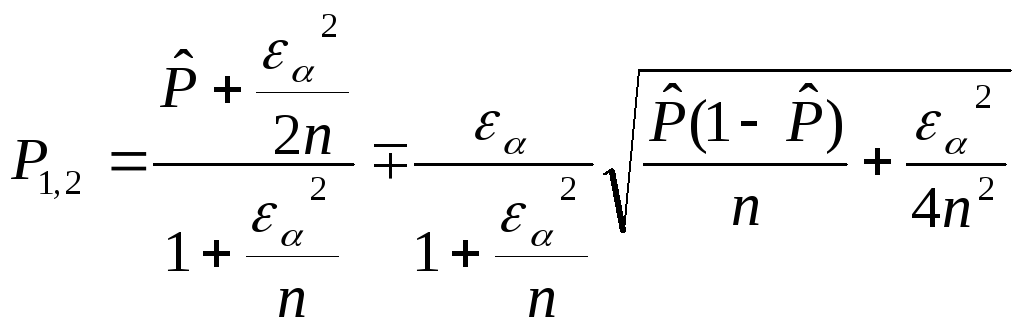
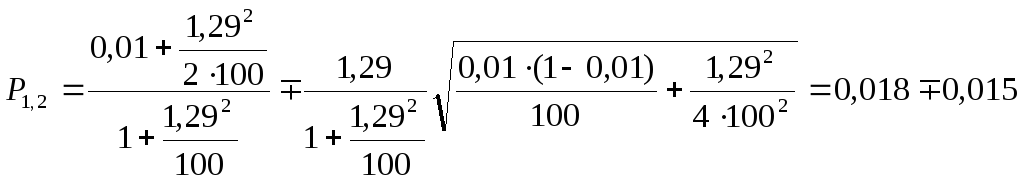
Искомый интервал для
![]() : 0,003
<
: 0,003
<
![]() < 0,033
< 0,033
-
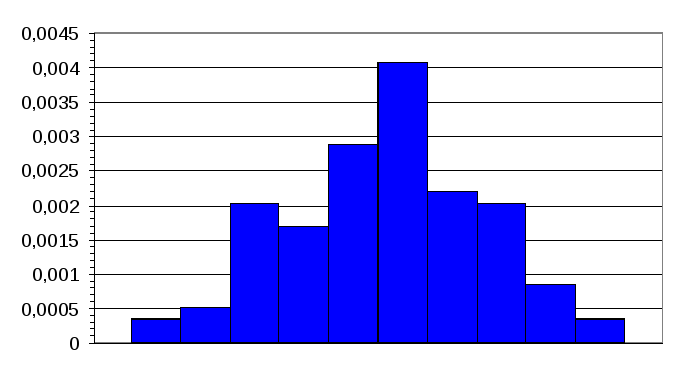
Построение гистограммы.
Заключаем все экспериментальные данные в интервал (-280;310). Разбиваем его на 10 равных разрядов, длиной 59.
|
Разряд (Хi-1,Xi) |
Частота попадания случайной величины Х в разряд |
Значение гистограммы
|
Доверительные границы для плотности распределения |
|
(-280;-221) |
0,02 |
0,00034 |
0,00009059 – 0,00153240 |
|
(-221;-162) |
0,03 |
0,00051 |
0,00016650 – 0,00179547 |
|
(-162;-103) |
0,12 |
0,00203 |
0,00115719 – 0,00385563 |
|
(-103;-44) |
0,1 |
0,00169 |
0,00090868 – 0,00342618 |
|
(-44;15) |
0,17 |
0,00288 |
0,00181852 – 0,00488922 |
|
(15;74) |
0,24 |
0,00407 |
0,00281348 – 0,00626714 |
|
(74;133) |
0,13 |
0,00220 |
0,00128528 – 0,00406653 |
|
(133;192) |
0,12 |
0,00203 |
0,00115719 – 0,00385563 |
|
(192;251) |
0,05 |
0,00085 |
0,00034957 – 0,00229037 |
|
(251;310) |
0,02 |
0,00034 |
0,00009059 – 0,00153240 |
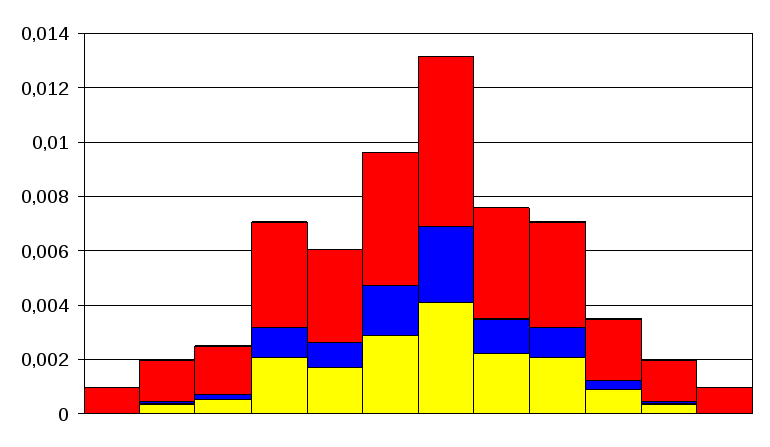
Гистограмма
Эмпирическая функция распределения
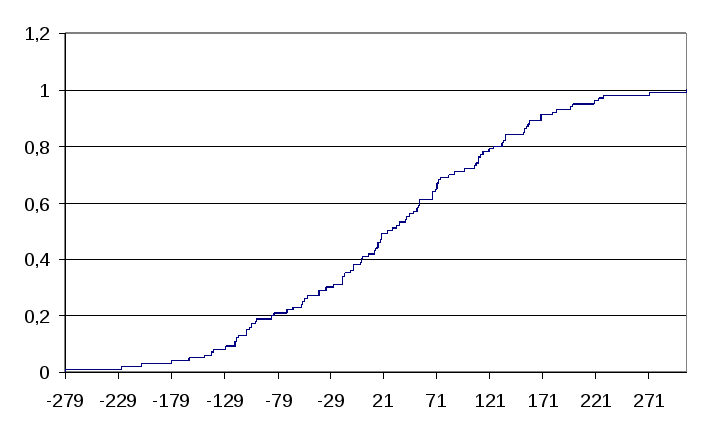
-
Доверительные области для плотности распределения и функции распределения.
![]()
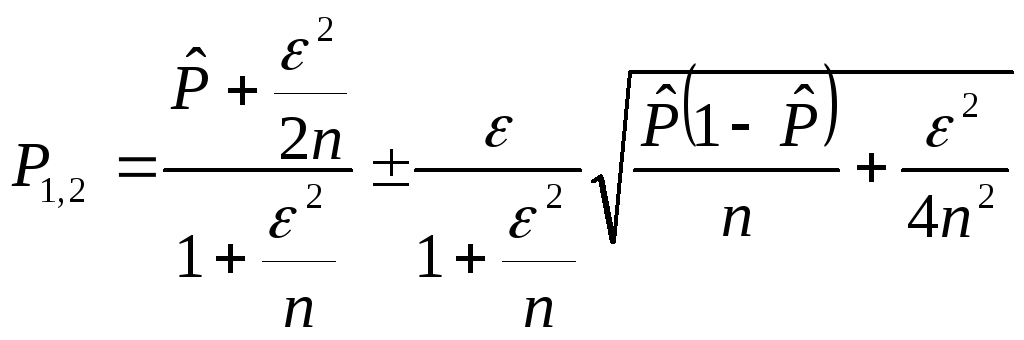
Гистограмма с доверительными областями
Доверительная область
для функции распределения F(x),
соответствующая коэффициенту доверия
![]()
![]() , по таблице значений
предельного распределения Колмогорова
определяем λ
= 1,21
, по таблице значений
предельного распределения Колмогорова
определяем λ
= 1,21
![]()
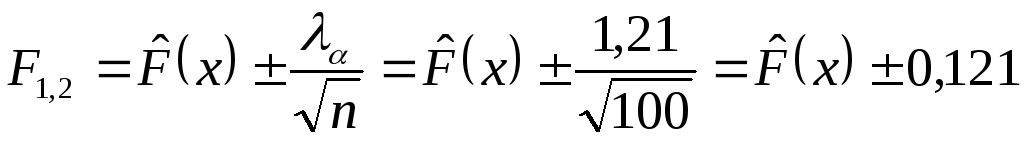
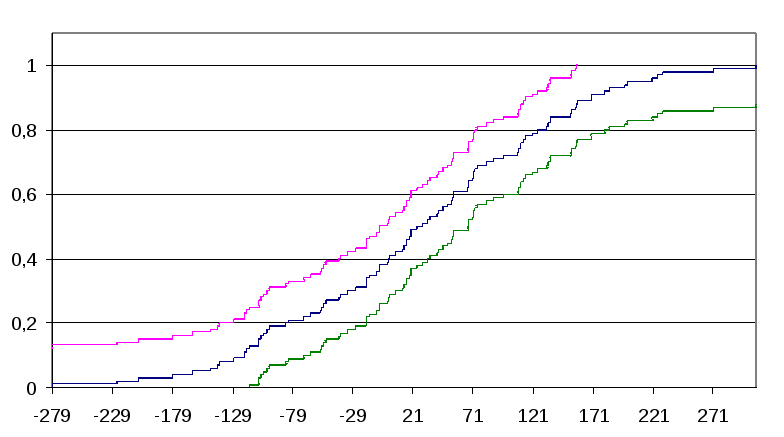
Эмпирическая функция распределения с доверительными интервалами
-
Сглаживание гистограммы и эмпирической функции распределения подходящим законом распределения
Сглаживание гистограммы нормальным законом распределения:
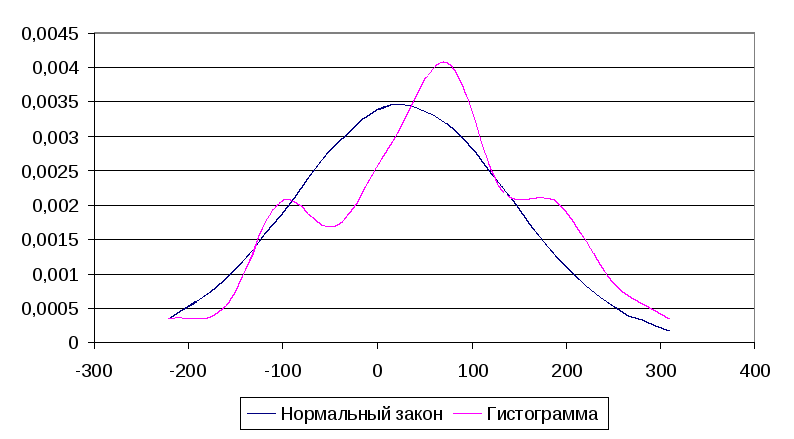
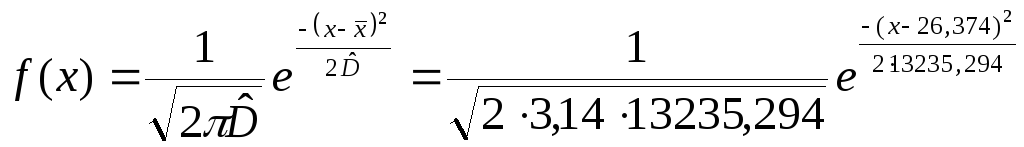
Сглаживание эмпирической функции:
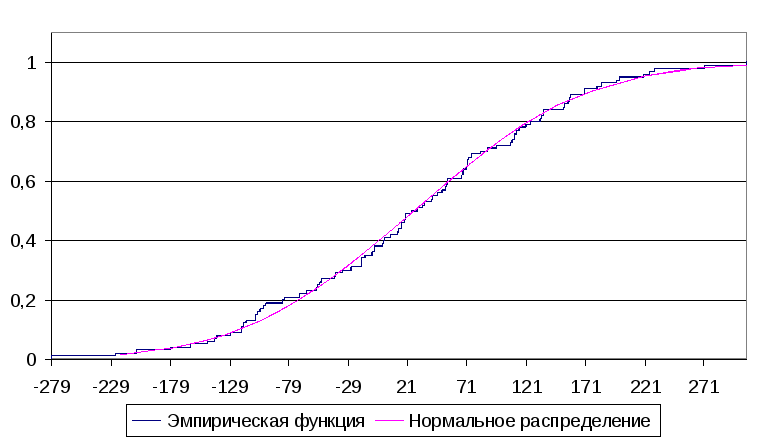
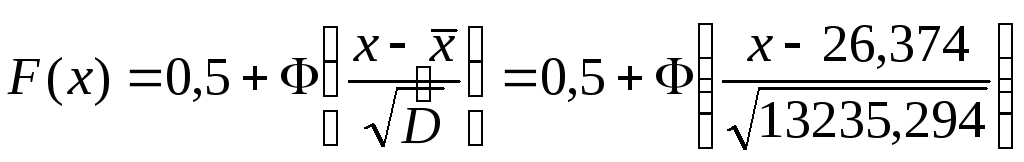
-
Проверка гипотезы о совпадении нормального закона распределения с истинным законом при уровне значимости
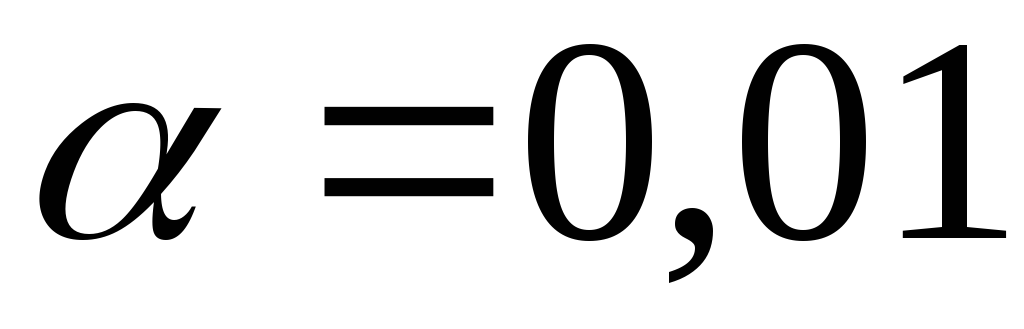 .
.
Проверка с использованием
![]() -
критерия.
-
критерия.
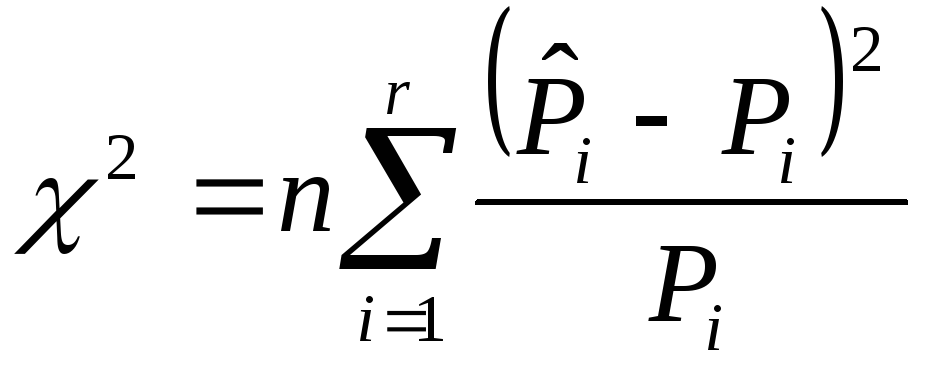 =
5,7597, где
=
5,7597, где
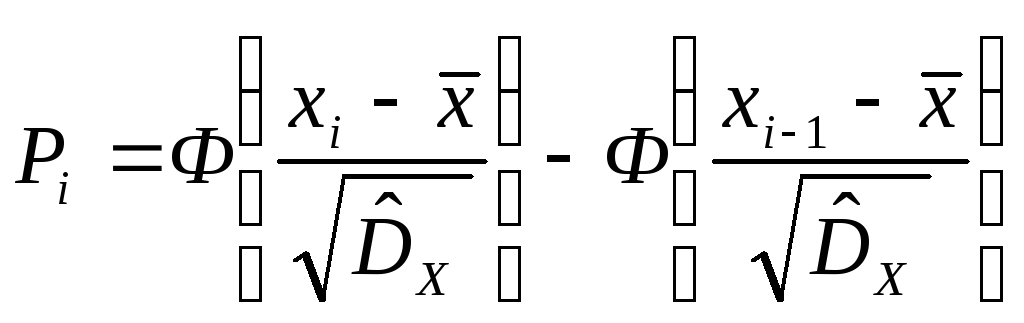
Число степеней свободы s = r – 1 – k = 12 – 1 – 2 = 9
![]() 2,188
2,188
Таким образом,
![]() и, следовательно, гипотеза по критерию
согласия
и, следовательно, гипотеза по критерию
согласия
![]() не является правдоподобной
не является правдоподобной
Проверка по критерию Колмогорова.
Максимальное различие между гипотетической и эмпирической функциями равно:
![]()
![]()
При уровне значимости
![]() критерий Колмогорова
критерий Колмогорова
![]()
Т. к.
![]() ,
гипотеза о том, что исследуемый закон
распределения является нормальным,
подтверждена и по критерию Колмогорова.
,
гипотеза о том, что исследуемый закон
распределения является нормальным,
подтверждена и по критерию Колмогорова.
