Prak_Geom1

Вiнницький державний педагогiчний унiверситет iменi Михайла Коцюбинського

Iнститут Математики, Фiзики та Технологiчно¨ Освiти

В. С. Трохименко

КОНСПЕКТ ЛЕКЦIЙ

З АНАЛIТИЧНОˆ ГЕОМЕТРIˆ

Вiнниця 2008

Трохименко Валентин Степанович, професор, кандидат фiз.-мат. наук.

В основi аналiтично¨ геометрi¨ лежить метод координат, який дозволя¹ розв'язувати геометричнi задачi засобами алгебри. Цей метод був вперше сформульований i систематично застосований Р. Декартом вiдомим французьким математиком XVII столiття. Суть його поляга¹ у тому, що на площинi або в просторi фiксу¹ться допомiжна геометрична фiгура, яка дозволя¹ довiльнiй точцi спiвставити деяку систему чисел, якi називають координатами точки. У бiльшостi випадкiв вихiдна допомiжна фiгура ¹ однi¹ю або декiлькома осями, тобто прямими, на яких вибрано певний напрямок. Такi осi називають координатними. Пiд системою координат розумiють вiдображення, яке точкам площини або простору за допомогою видiлено¨ допомiжно¨ фiгури ставить у вiдповiднiсть системи чисел, якi однозначно визначають розташування точки вiдносно цi¹¨ фiгури.

Довiльна геометрична фiгура завжди розгляда¹ться як множина точок, якi мають певну властивiсть, що властива тiльки точкам цi¹¨ фiгури i жодним iншим. Це наклада¹ певнi обмеження на координати точок, що належать геометричнiй фiгурi, що на мовi алгебри означа¹: координати точок геометрично¨ фiгури задовольняють деяке певне рiвняння або систему рiвнянь. Таким чином, якщо на площинi або в просторi фiксована деяка система координат, то точцi вiдповiда¹ набiр чисел ¨¨ координати, а лiнiям та поверхням рiвняння або системи рiвнянь, яким задовольняють координати точок цi¹¨ геометрично¨ фiгури.

Аналiтична геометрiя органiчно по¹днала геометрiю з алгеброю та математичним аналiзом, що привело згодом до прогресу в розвитку математики та ¨¨ застосувань до природничих наук. Аналiтична геометрiя це такий роздiл геометрi¨, в якому геометричнi фiгури вивчаються за допомогою алгебри на основi використання координат. Для цього фiгура пода¹ться рiвняннями або нерiвностями в координатах у такому розумiннi це ¹ так звана перша задача аналiтично¨ геометрi¨.

В аналiтичну геометрiю входить також друга задача, обернена до першо¨: дослiдити, якi геометричнi фiгури подаються тими чи iншими рiвняннями.

На деннiй формi навчання передбача¹ться вивчення аналiтично¨ геометрi¨ на площинi та в просторi, загально¨ теорi¨ лiнiй i поверхонь другого порядку, перетворень площини i простору протягом перших двох семестрiв. У першому семестрi вивчаються елементи векторно¨ алгебри, метод координат на площинi, пряма лiнiя на площинi, конiчнi перерiзи, загальна теорiя лiнiй другого порядку та геометричнi перетворення площини. В другому семестрi вивча¹ться метод координат у просторi, теорiя прямих i площин у просторi, поверхнi другого порядку за ¨х канонiчними рiвняннями, загальна теорiя поверхонь другого порядку та геометричнi перетворення простору.

Конспект лекцiй вiдповiда¹ дiючiй програмi з аналiтично¨ геометрi¨ для математичних спецiальностей педагогiчних унiверситетiв. Ним можуть користуватись не тiльки студенти стацiонарного вiддiлення, але й заочного, та особи, якi вивчають цей курс самостiйно.

Çìiñò

1 Елементи векторно¨ алгебри. Геометрiя на площинi			6
1.1	Елементи векторно¨ алгебри в просторi . . . . . . . . . . . . . . . . . . .		6
	1	Вектори. Лiнiйнi операцi¨ над векторами . . . . . . . . . . . . . . . . . .	6
	2	Лiнiйна залежнiсть векторiв . . . . . . . . . . . . . . . . . . . . . . . . .	11
	3	Скалярний добуток векторiв . . . . . . . . . . . . . . . . . . . . . . . . .	16
	4	Векторнi пiдпростори . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	18
1.2	Метод координат на площинi . . . . . . . . . . . . . . . . . . . . . . . . . .		20
	1	Афiнна система координат на площинi . . . . . . . . . . . . . . . . . . .	20
	2	Орi¹нтацiя площини . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	23
	3	Перетворення афiнних координат. Полярнi координати . . . . . . . . .	26
1.3 Пряма лiнiя на площинi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .			30
	1	Рiвняння прямо¨ на площинi . . . . . . . . . . . . . . . . . . . . . . . . .	30
	2	Загальне рiвняння прямо¨ на площинi . . . . . . . . . . . . . . . . . . . .	31
	3	Кут мiж двома прямими на площинi . . . . . . . . . . . . . . . . . . . .	34
	4	Основнi задачi на пряму в площинi . . . . . . . . . . . . . . . . . . . . .	35
1.4	Перетворення площини . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		38
	1	Вiдображення i перетворення множин . . . . . . . . . . . . . . . . . . .	38
	2	Рух площини . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	40
	3	Два види руху. Аналiтичне задання руху площини . . . . . . . . . . . .	44
	4	Класифiкацiя рухiв площини . . . . . . . . . . . . . . . . . . . . . . . . .	47
	5	Група рухiв площини та ¨¨ пiдгрупи . . . . . . . . . . . . . . . . . . . . .	50
	6	Група симетрiй геометрично¨ фiгури . . . . . . . . . . . . . . . . . . . .	53
	7	Перетворення подiбностi . . . . . . . . . . . . . . . . . . . . . . . . . . .	55
	8	Афiннi перетворення площини . . . . . . . . . . . . . . . . . . . . . . . .	58
	9	Перспективно-афiннi перетворення площини . . . . . . . . . . . . . . . .	61
	10	Група афiнних перетворень та ¨¨ пiдгрупи. Афiнна еквiвалентнiсть фiгур	63
1.5	Вивчення лiнiй другого порядку за канонiчними рiвняннями . . . . .		65
	1	Åëiïñ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	65
	2	Гiпербола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	70
	3	Парабола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	73
	4	Рiвняння елiпса, гiперболи i параболи в полярних координатах . . . . .	75
1.6	Загальна теорiя лiнiй другого порядку . . . . . . . . . . . . . . . . . . . .		78
	1	Загальне рiвняння лiнi¨ другого порядку . . . . . . . . . . . . . . . . . .	78
	2	Перетин лiнi¨ другого порядку з прямою . . . . . . . . . . . . . . . . . .	79
	3	Асимптотичнi напрямки лiнi¨ другого порядку . . . . . . . . . . . . . .	81
	4	Центр лiнi¨ другого порядку . . . . . . . . . . . . . . . . . . . . . . . . .	82
	5	Дотична до лiнi¨ другого порядку . . . . . . . . . . . . . . . . . . . . . .	84
	6	Дiаметри лiнi¨ другого порядку. Спряженi напрямки . . . . . . . . . . .	86

3

	7	Головнi напрямки i головнi дiаметри лiнi¨ другого порядку . . . . . . .	88
	8	Класифiкацiя лiнiй другого порядку . . . . . . . . . . . . . . . . . . . .	89
	9	Зведення рiвняння лiнi¨ другого порядку до канонiчного виду . . . . .	90
2 Геометрiя в просторi: площини, прямi лiнi¨, поверхнi			95
другого порядку
2.1	Метод координат в просторi. Мiшаний та векторний добутки векторiв		95
	1	Координати точок в просторi . . . . . . . . . . . . . . . . . . . . . . . .	95
	2	Орi¹нтацiя простору . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	96
	3	Перетворення афiнних координат в просторi . . . . . . . . . . . . . . . .	99
	4	Мiшаний добуток векторiв. Об'¹м тетраедра . . . . . . . . . . . . . . . .	102
	5	Векторний добуток векторiв. Площа трикутника . . . . . . . . . . . . .	104
2.2	Площини i прямi в просторi . . . . . . . . . . . . . . . . . . . . . . . . . . .		107
	1	Рiвняння площини . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	107
	2	Геометричний змiст нерiвностi Ax + By + Cz + D > 0 . . . . . . . . . .	109
	3	Вза¹мне розташування двох i трьох площин . . . . . . . . . . . . . . . .	110
	4	Вiдстань вiд точки до площини. Кут мiж площинами . . . . . . . . . .	112
	5	Рiвняння прямо¨ в просторi . . . . . . . . . . . . . . . . . . . . . . . . . .	114
	6	Вза¹мне розташування двох прямих, прямо¨ i площини . . . . . . . . .	116
	7	Кути мiж двома прямими, мiж прямою i площиною . . . . . . . . . . .	117
	8	Основнi задачi на пряму i площину . . . . . . . . . . . . . . . . . . . . .	118
2.3	Перетворення простору . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		122
	1	Рух простору . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	122
	2	Два види руху. Iнварiантнi точки прямi та площини . . . . . . . . . . .	123
	3	Класифiкацiя рухiв простору . . . . . . . . . . . . . . . . . . . . . . . . .	125
	4	Перетворення подiбностi простору . . . . . . . . . . . . . . . . . . . . . .	127
	5	Афiннi перетворення простору . . . . . . . . . . . . . . . . . . . . . . . .	129
2.4 Вивчення поверхонь другого порядку за канонiчними рiвняннями . .			132
	1	Поверхнi другого порядку. Метод перерiзiв . . . . . . . . . . . . . . . .	132
	2	Поверхнi обертання . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	133
	3	Цилiндричнi та конiчнi поверхнi другого порядку . . . . . . . . . . . . .	135
	4	Åëiïñî¨ä . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	147
	5	Гiперболо¨ди . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	149
	6	Параболо¨ди . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	152
	7	Прямолiнiйнi твiрнi поверхонь другого порядку . . . . . . . . . . . . . .	154
2.5	Загальна теорiя поверхонь другого порядку . . . . . . . . . . . . . . . .		157
	1	Перетин поверхнi другого порядку з прямою . . . . . . . . . . . . . . .	157
	2	Асимптотичнi напрямки поверхнi другого порядку . . . . . . . . . . . .	158
	3	Центр поверхнi другого порядку . . . . . . . . . . . . . . . . . . . . . . .	159
	4	Дiаметральнi площини поверхонь другого порядку . . . . . . . . . . . .	161
	5	Центр плоского перерiзу та дiаметри поверхнi . . . . . . . . . . . . . . .	163
	6	Дотична площина i нормаль до поверхнi другого порядку . . . . . . . .	164
	7	Спрощення рiвняння поверхнi другого порядку за допомогою обертання
		системи координат навколо початку . . . . . . . . . . . . . . . . . . . .	166
	8	Спрощення рiвняння поверхнi другого порядку за допомогою
		паралельного перенесення системи координат . . . . . . . . . . . . . . .	169
	9	Iнварiанти поверхонь другого порядку. Класифiкацiя поверхонь за
		допомогою iнварiантiв . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	173

4

Лiтература	176
Покажчик	177

5

Ðîçäië 1

Елементи векторно¨ алгебри. Геометрiя на площинi

1.1 Елементи векторно¨ алгебри в просторi

1 Вектори. Лiнiйнi операцi¨ над векторами

Направленi вiдрiзки та ¨х еквiполентнiсть. Вектори. Додавання та вiднiмання векторiв, ¨х властивостi. Множення вектора на число та його властивостi.

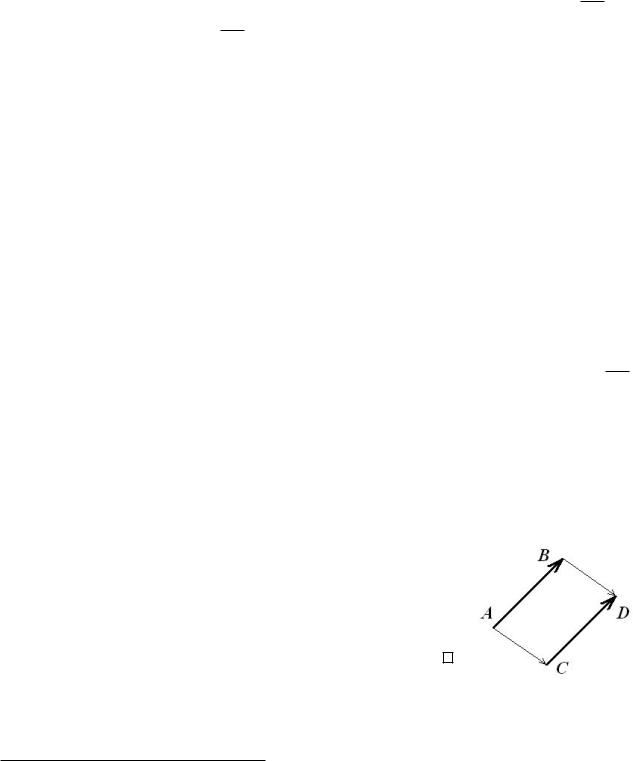
Направленi вiдрiзки та ¨х еквiполентнiсть. Вектори. Вiдомо ще з середньо¨ школи, що направленим вiдрiзком ми назива¹мо вiдрiзок, у якого один з його кiнцiв прийма¹ться за початок, а iнший за кiнець. Якщо початок вiдрiзка позначити через A, à êiíåöü

через B, то такий направлений вiдрiзок ми позначатимемо як AB. Таким чином, на вiдрiзку встановлю¹ться напрямок вiд точки A до точки B. Направленi вiдрiзки AB i BA називаються протилежними, а направлений вiдрiзок AA назива¹ться нульовим. Довжина направленого вiдрiзка AB познача¹ться як jABj або просто як AB. Довжина нульового направленого вiдрiзка вважа¹ться такою, що дорiвню¹ нулевi, тобто jAAj = 0.

Якщо направленi	âiäðiçêè	AB	i	CD		мають однаковi напрямки, то ми назива¹мо
¨х спiвнаправленими	i познача¹мо це			ÿê			·		, а якщо вони мають протилежнi
						AB		CD

напрямки, то назива¹мо ¨х протилежно направленими i познача¹мо AB "# CD. Очевидно,

що спiвнаправленi i протилежно

направленi вiдрiзки

лежать на

паралельних

ïðÿìèõ.

Якщо направленi вiдрiзки AB i

мають однаковi напрямки i

CD

рiвнi довжини, то

¨х називають

еквiполентними

i

позначають

öåé ôàêò

ÿê

AB

!

CD.

=

Символiчно це запису¹ться так:

!

def

AB

CD;

:

AB = CD () (

AB·= CD

j

j

j

Зазначимо деякi властивостi еквiполентних вiдрiзкiв:

j

!

1±: AB = AB для довiльних точок A; B (рефлексивнiсть),

!

!

2±: AB = CD =

CD = AB для довiльних точок A; B; C; D (симетричнiсть),

)

!

!

!

довiльних

точок A; B; C; D; E; F

3±: AB = CD

^

CD = EF

= AB = EF äëÿ

)

(транзитивнiсть).

6

Таким чином, вiдношення	еквiполентностi !
вiдношення еквiполентностi	= ¹ вiдношенням еквiвалентностi.1 Îòæå,
	!
	= розбива¹ множину всiх направлених вiдрiзкiв на класи, якi

не мають мiж собою спiльних елементiв, i кожен з них мiстить всi еквiполентнi мiж собою направленi вiдрiзки. Кожний з таких класiв назива¹ться вектором. Отже, клас [AB]!

=, ÿêèé

¡¡!

мiстить направлений вiдрiзок AB, ¹ вектор, що познача¹ться через AB . Таким чином, ми приходимо до такого означення вектора:

Означення 1.1.

¡¡!

Вектором

AB назива¹ться клас усiх направлених вiдрiзкiв, еквiполент-

них направленому вiдрiзку AB.

З цього означення виплива¹, що

¡¡! ¡¡!

!

(1.1)

!

!

AB = CD () AB = CD () AB · CD ^ jABj = jCDj () [AB]=

= [CD]=:

¡¡!

¡¡! ¡¡!

Îòæå, ÿêùî

CD

2 AB , то це означа¹, що

AB = CD . Пiд напрямком i довжиною вектора

¡¡!

ми розумi¹мо напрямок i довжину довiльного направленого вiдрiзка з класу

AB

!

[AB]=.

Таким чином, виходячи з (1.1) ми можемо сказати, що

¡¡!

¡¡!

¡¡! ¡¡! ¡¡!

¡¡!

AB = CD () AB · CD ^ j AB j = jCD j ()

AB

·

CD

^ AB = CD;

(1.2)

тобто два вектори рiвнi, коли вони мають однаковi напрямки та однаковi довжини. Надалi ,~

позначатимемо вектори також однi¹ю лiтерою, наприклад, ~a b, ~c : : : i у випадку, коли AB 2 ~a,

¡¡!

то писатимемо ~a = AB , при цьому казатимемо, що ми вiд точки A вiдклали вектор ~a i отримали точку B. Протилежний вектор до вектора ~a позначатимемо через ¡~a. Таким чином,

¡~a =

BA

.

i~

~

Вектори ~a

b називаються колiнеарними (познача¹ться як ~a k b), якщо вони спiвнаправленi

або протилежно направленi, тобто

~

~

~

(1.3)

~a k b () ~a · b _ ~a "# b:

Ëåìà 1.1. ßêùî

¡¡!

¡¡!

¡¡! ¡¡!

AB = CD , òî AC = BD .

Доведення. Оскiльки

¡¡!

¡¡!

AB = CD , то чотирикутник ABDC

паралелограм, тому AC = BD i AC · BD. Îòæå, çãiäíî ç

(1.2) ìà¹ìî

¡¡!

¡¡!

AC = BD .

Вектор ~a назива¹ться одиничним, якщо його

довжина дорiвню¹ одиницi, тобто

.

0

j~aj = 1

Ортом вектора ~a назива¹ться такий одиничний вектор ~a

, який спiвнаправлений з ~a, тобто

j~a

0

j = 1

i

0

. Нульовий вектор ¡¡!, äå

довiльна точка, познача¹ться через ~.

~a

· ~a

AA

A

0

1 Нагада¹мо, що бiнарне вiдношення " ½ A £ A назива¹ться вiдношенням еквiвалентностi, якщо воно рефлексивне, симетричне i транзитивне, тобто задовольня¹ вiдповiдно такi умови: 1. (8a 2 A)(a; a) 2 " (рефлексивнiсть), 2. (8a; b 2 A)((a; b) 2 " ¡! (b; a) 2 ") (симетричнiсть), 3. (8a; b; c 2 A)((a; b) 2 " ^ (b; c) 2 " ¡! (a; c) 2 ") (транзитивнiсть). Вiдношення еквiвалентностi " розбива¹ множину A на, так званi, класи

еквiвалентностi [a]" = fb 2 A j (a; b) 2 "g; a 2 A, якi попарно не мають спiльних елементiв, при цьому ма¹ мiсце спiввiдношення: (a; b) 2 " () [a]" = [b]".

7

¡¡! ¡¡!

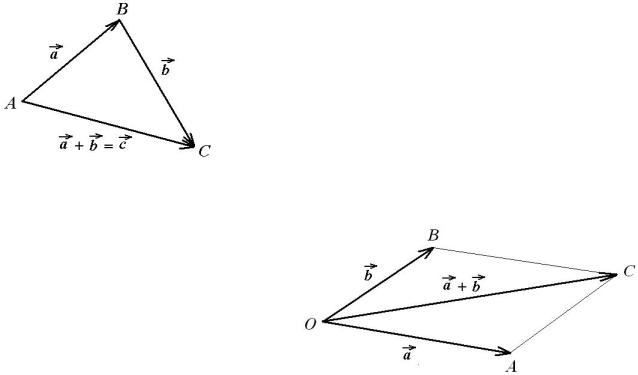
Додавання та вiднiмання векторiв. Додавання векторiв викону¹ться за правилом
трикутникiв або за правилом паралелограма. Отже, нехай ~a		i ~
		b ¹ деякi вектори, потрiбно
~
визначити вектор ~c, який ¹ ¨х сумою, тобто ~c = ~a + b. Щоб додати два вектори за правилом
трикутника необхiдно вибрати довiльну точку A i
вiдкласти вiд не¨ вектор ~a. Ми отрима¹мо точку B. Îòæå,
¡¡!			вiдклада¹мо		вектор ~
~a = AB . Потiм вiд точки B					b i
отриму¹мо точку C	. Таким чином, ~			¡¡!
			b = BC . Тодi вектор
¡¡!			i ~
~c = AC i ¹ сумою векторiв ~a			b. Правило трикутника
записують у векторнiй формi так:
	¡¡!	¡¡!	¡¡!		(1.4)
	AB + BC = AC :

Тепер розглянемо додавання векторiв за правилом паралелограма. В цьому випадку ми вiд-

клада¹мо

обидва

вектори ~a

i ~

b âiä

деяко¨ наперед вибрано¨ точки O. Â

результатi ма¹мо точки A i B, äå

¡¡! i

~

¡¡!

~a = OA

b = OB . На векторах, як

на сторонах, буду¹мо паралелограм

OACB. ßñíî, ùî

¡¡!

~

AC = b, îñêiëüêè

цi вектори мають рiвнi довжини i

напрямки. Тепер ми бачимо, що за

правилом трикутника

~

¡¡!

¡¡!

¡¡!

OC = OA + AC = ~a + b.

¡¡!

¡¡!

¡¡!

¡¡!

¡¡!

¡¡!

¡¡!

Нехай ~a = AB , òîäi çãiäíî ç (1.4) ìà¹ìî

AB

+ BB = AB i

AA

+ AB = AB . Îòæå,

~

i ~

. Оскiльки також

¡¡!

¡¡! ¡¡!, òî

~

. Аналогiчно

~a + 0 = ~a

0 + ~a = ~a

~.

AB + BA = AA

~a + (¡~a) = 0

доводиться, що

(¡~a) + ~a = 0

~

Теорема 1.1. Для довiльних векторiв ~a; b;~c мають мiсце такi рiвностi:

1±: ~a +~b = ~b + ~a (комутативний закон),

2±: (~a +~b) + ~c = ~a + (~b + ~c) (асоцiативний закон).

Доведення. З останнього рисунка ми бачимо, що

¡¡!

¡¡!

¡¡!

~

¡¡! ¡¡!

OC = OA + AC = ~a+b, а також OC = OB

¡¡! ~

~

~

+ BC = b + ~a. Оскiльки лiвi частини рiвнi, то ~a + b = b + ~a. Комутативнiсть доведена.

~

Для доведення асоцiативностi розглянемо три вектори ~a; b;~c. Виберемо довiльну точку A i

¡¡!

вiдкладаючи вiд не¨ вектор ~a отрима¹мо точку B, тобто ~a = AB . Далi вiд точки B вiдкладемо

вектор~		, тобто~	¡¡!			¡¡!
	b i матимемо точку C	b = BC . I нарештi, вiд точки C вiдкладемо вектор ~c = CD
			~	¡¡!	¡¡!	¡¡!
i одержимо точку D. За правилом трикутника (1.4) ма¹мо ~a + b = AB					+ BC = AC . Àëå
¡¡!	¡¡! ¡¡!	~	¡¡!. Аналогiчно ма¹ мiсце ~		¡¡!	¡¡! ¡¡!
AC	+ CD = AD , òîìó (~a + b) + ~c = AD			b + ~c = BC + CD = BD .

¡¡!

Äàëi ìà¹ìî AB + BD = AD ми довели асоцiативний закон

~

¡¡!

, тобто справедлива рiвнiсть ~a + (b + ~c) = AD . Таким чином,

~ ~

(~a + b) + ~c = ~a + (b + ~c):

8

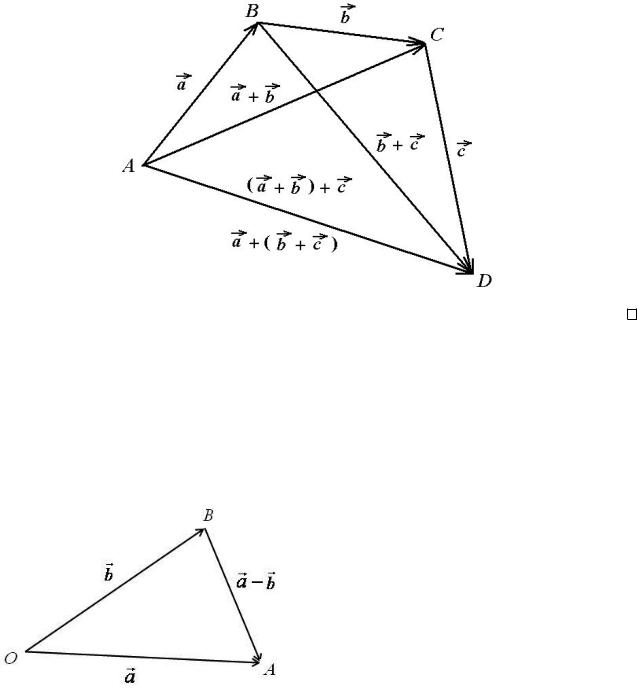
Враховуючи асоцiативний закон, неважко бачити, що для довiльних точок A1, A2, A3, A4; : : :, An¡2, An¡1, An викону¹ться рiвнiсть

¡¡! ¡¡! ¡¡! ¡¡! ¡¡! ¡¡!

A1A2 + A2A3 + A3A4 + : : : + An¡2An¡1 + An¡1An=A1An :

Означення 1.2. Рiзницею векторiв ~a

~

цьому записують ~x = ~a ¡ b.

i ~			, ùî ~
b назива¹ться такий вектор ~x			b + ~x = ~a, ïðè
ßêùî O деяка довiльно вибрана точка
¡¡!,	à ~	¡¡!	~	¡¡!
i ~a = OA	b	= OB ,	òî ~a ¡ b	= BA .

Словесно правило вiднiмання векторiв можна
сформулювати так: для того щоб вiд вектора
~a	вiдняти	вектор ~
		b необхiдно ¨х вiдкласти

вiд деяко¨ фiксовано¨ точки O, тодi початок

рiзницi цих векторiв	~	буде знаходитись
в кiнцi вектора ~	~a ¡ b
b, à êiíåöü ðiçíèöi ó êiíöi

вектора ~a (див. рис.). А тепер доведемо

ðiâíiñòü:	~	~
	~a ¡ b = ~a + (¡b):

~, тобто ~		, òîìó ~		~	~
Нехай ~x = ~a ¡ b	b + ~x = ~a		b + ~x + (¡b) = ~a + (¡b). Користуючись тепер
комутативним законом, будемо мати ~			~	~	, тобто ~	~	. Îòæå,
		b + (¡b) + ~x = ~a + (¡b)			0 + ~x = ~a + (¡b)

~

~x = ~a + (¡b). Доведiть самостiйно такi спiввiдношення:

~	~
j~a + bj 6 j~aj + jbj;
~	~

j~a ¡ bj 6 j~aj + jbj:

(1.5)

(1.6)

Множення вектора на число та його властивостi. Нехай ~a довiльний вектор i

® довiльне дiйсне число. Визначимо операцiю множення числа на вектор так:

9

Означення 1.3. Добутком вектора ~a

на число

®

назива¹ться такий вектор p~

(познача¹ться ®~a), який задовольня¹ умови:

1) jp~j = j®jj~aj;

2) p~ · ~a; ÿêùî ® > 0;

i p~ "# ~a; ÿêùî ® < 0;

ÿêùî

òî

~

3)

® = 0;

0~a = 0:

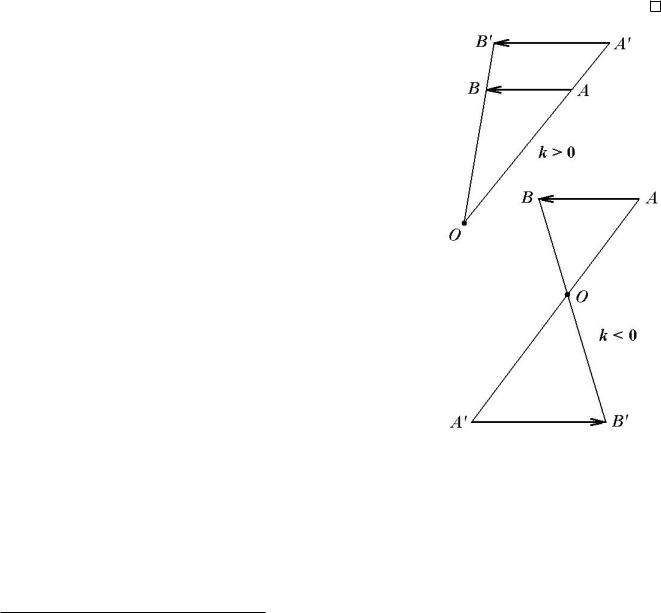
Ëåìà

1.2. ßêùî

при гомотетi¨

ç

центром O i

êîåôiöi¹íòîì k трикутник OAB

переходить у трикутник OA0B0

, òî

¡¡!

¡¡!

A0B0= k AB .

Доведення. За означенням гомотетi¨ 2

¡¡!

¡¡!

¡¡!

¡¡!

ìà¹ìî OA0 = k OA i OB0

= k OB , звiдки виплива¹

OA0 =

j

k

OA i OB0

=

j

k OB. Отже, трикутники OAB i OA0B0 подiбнi за першою ознакою

j

j

¡¡!

¡¡!

подiбностi, тому A0B0

= jkjAB i A0B0kAB. Таким чином, A0B0= k AB .

Теорема 1.2. Для довiльних чисел ®; ¯

~

i векторiв ~a; b

виконуються такi рiвностi:

1±:

1

¢

~a = ~a; (

¡

1)

¢

~a = ~a;

2±:

¡

®(¯~a) = (®¯)~a (закон асоцiативностi);

3±:

®(~a +~b) = ®~a + ®b~ (1-й закон дистрибутивностi);

4±:

(® + ¯)~a = ®~a + ¯~a (2-й закон дистрибутивностi):

Доведення. Властивiсть 1± безпосередньо виплива¹ з озна-

чення 1.3 множення вектора на число.

2±: Введемо такi позначення: p~ = ®(¯~a) i ~q = (®¯)~a. За означенням 1.3 ма¹мо jp~j = j®(¯~a)j = j®jj¯~aj = j®jj¯jj~aj;

j~qj = j®¯jj~aj = j®jj¯jj~aj, òîìó jp~j = j~qj. Доведемо, що p~ · ~q.

Можливi два випадки: ®¯ > 0 i ®¯ < 0. У першому з них числа ® i ¯ мають однаковi знаки, тому p~ · ~a, àëå i ~q · ~a, тому в даному разi p~ · ~q. У другому випадку числа ® i ¯ мають рiзнi знаки, тому p~ "# ~a i ~q "# ~a. Отже, i в цьому

випадку p~ · ~q. Таким чином, вектори p~ i ~q мають рiвнi

довжини i однаковi напрямки, тому згiдно з (1.2) вони рiвнi, тобто p~ = ~q.

			¡¡!
3±: Вiдкладемо вiд деяко¨ довiльно вибрано¨ точки A вектор AB = ~a, а потiм вiд точки
¡¡!	~	¡¡!	~
B вектор BC = b, òîäi		AC = ~a + b. Розглянемо гомотетiю з коефiцi¹нтом ® i з центром у

äîâiëüíié òî÷öi O, яка не лежить на сторонах трикутника ABC. Нехай при данiй гомотетi¨

A A0, B		B0	, C C0, тодi згiдно з лемою 1.2 ма¹мо				¡¡!
7!		7!	7! ¡¡!	¡¡! ¡¡!	¡¡!	¡¡!
	¡¡!		A0B0	= ® AB ; B0C0	= ® BC ; A0C0= ® AC ;
			¡¡!	¡¡!	¡¡!	¡¡!	¡¡!
тобто	A0B0	= ®~a, B0C0= ®b~, A0C0= ®(~a +~b). Àëå A0B0				+ B0C0	=A0C0, тобто ®~a + ®b~ = ®(~a +~b).

4±: Можливi два випадки: а) ®¯ > 0 i á) ®¯ < 0. Розглянемо кожний з них окремо.

2 Нагада¹мо, що гомотетi¹ю з центром в точцi O i êîåôiöi¹íòîì k =6 0 назива¹ться таке перетворення, при

¡¡! ¡¡!

якому точка M переходить у таку точку M0, що викону¹ться рiвнiсть OM0= k OM .

10