Лаб. 1

Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Сибирский федеральный университет»

Институт инженерной физики и радиоэлектроники

Кафедра общей физики

Л. М. Образцова, Л. Т. Сухов

ОБЩАЯ ФИЗИКА ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Лабораторная работа 1

Изучение электростатических и электрических полей

Методические указания

Красноярск 2011

Изучение электростатических и электрических полей

Цели работы:

исследовать структуры электростатических полей, создаваемых заряженными электродами простых симметричных форм, и электрических полей, возникающих при протекании электрического тока через слабый электролит;

построить силовые линии поля по найденным линиям равного потенциала.

Теоретические сведения

Принято считать, что всякий электрический заряд определенным образом изменяет окружающее его пространство – создает вокруг себя электрическое поле. Это поле обнаруживается по силе, действующей на электрический заряд q, помещаемый в любую точку пространства. Величина силы F определяется законом Кулона:

F q E.

(1.1)

Векторная величина E называется напряженностью электрического поля в данной точке пространства. Напряженность E можно определить как силу, действующую на положительный единичный заряд:

	F	.	(1.2)
E	q

Поля неподвижных зарядов называются электростатическими.

Если имеется более двух зарядов, то суммарная сила, действующая на любой заряд из данной совокупности зарядов, будет определяться суммой сил парных взаимодействий этого заряда со всеми остальными по закону Кулона (1.1). Это утверждение следует из опытов и называется принципом суперпозиции. Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, созданных каждым из зарядов в отдельности:

E Ei .

(1.3)

Из принципа суперпозиции следует, что если имеется два заряда q1 и q2, помещенных в какую-либо непроводящую среду, то помимо их непосредственного взаимодействия необходимо учитывать также взаимодействие этих зарядов с зарядами электронов и атомных ядер, входящих в состав нейтральных молекул среды. В СИ, исходя из закона Кулона, напряженность поля неподвижного заряда q на расстоянии r от него можно представить как

Рис. 1.1. Силовые линии

	1 q
E				er ,	(1.4)
	4 0		r 2
где 0 – электрическая постоянная, равная				8,85 10-12 Ф/м; – диэлектриче-
ская проницаемость вещества окружающей среды; er					– орт радиус-вектора

r , проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Соотношения (1.3) и (1.4) позволяют вычислять напряженность поля любой системы зарядов, представив ее в виде совокупности точечных зарядов.

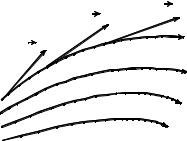
Электрическое поле можно описать, указав для каждой точки пространства величину и направление вектора E . Совокупность этих векторов образует поле вектора напряженности электрического поля. Зрительный образ электрического поля можно получить, проведя линии напряженности (их также называют силовыми линиями) так, чтобы касательная к ним в каждой точке совпадала с направлением вектора E . Густота линий выбирается такой, чтобы количество линий, пересекающих единицу поверхности, перпендикулярной к линиям, было равно числовому значению вектора E . Тогда по картине линий напряженности можно судить о направлении и величине вектора E в разных точках пространства (рис. 1.1).

	Для точечных зарядов линии поля будут	Е	Е
	представлять собой радиальные прямые, направ-
	ленные от заряда, если он положителен, и к заряду,	Е
	если он отрицателен (рис. 1.2). Линии одним кон-
	цом опираются на заряд, другим уходят в беско-
	нечность. Число линий, пересекающих поверх-

ность симметрично построенной сферы произвольного радиуса, будет всегда постоянно. Отсюда вытекает, что линии ни-

где, кроме заряда, не начинаются и не заканчиваются. Начавшись на заряде, они уходят в бесконечность (заряд положителен), либо, приходя из бесконечности, они заканчиваются на заряде (заряд отрицателен). Это свойство линий E является общим для всех электростатических полей.

С точки зрения математики электрическое поле E , как и поле любой другой векторной функции (например, поле вектора скорости), можно харак-

теризовать двумя свойствами: потоком вектора E и циркуляцией вектора E .

Пользуясь только этими двумя понятиями, можно описать все законы и электричества, и магнетизма.

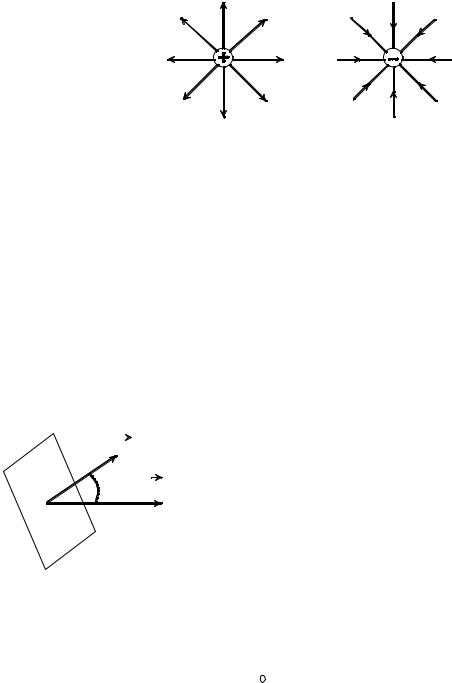
Рис. 1.2. Силовые линии точечных зарядов

Поток вектора E . Примем плотность линий равной модулю E . Тогда количество силовых линий dФ, пересекающих произвольную площадку dS,

вектор нормали n	к которой составляет угол с направлением E , определя-
ется выражением (рис. 1.3):
			d | E | dS cos ,
			d En dS
или
где Еn – проекция вектора			d EdS ,		(1.5)
		E	на нормаль n к площадке dS;	dS	– вектор, мо-
n	дуль которого равен dS, а направление				совпадает	с
	нормалью n к площадке (рис. 1.3).
	E	Величину dФ называют потоком			вектора	E
	сквозь площадку dS. Для замкнутой поверхности S в

dS	вакууме имеет место теорема Гаусса: поток вектора
	E	сквозь произвольную замкнутую поверхность равен

Рис. 1.3. К определению	алгебраической сумме зарядов внутри этой поверхно-
потока вектора E	сти, деленной на 0. Математически теорема Гаусса
	записывается так:
		1
	S EdS		qвнутр ,	(1.6)
		0

где кружок у интеграла означает, что интегрирование производится по замкнутой поверхности. Из теоремы Гаусса следует, что в то время как само поле E зависит от конфигурации всех зарядов как внутри, так и снаружи выбранной поверхности, поток вектора E определяется только алгебраической суммой зарядов, находящихся внутри поверхности S. От конфигурации внутренних зарядов поток E не зависит.

Теорема Гаусса позволяет достаточно легко рассчитать поле зарядов, если они находятся на электродах симметричной формы (плоской, цилиндрической или сферической). В этом случае удается подобрать такую поверх-

ность S, на которой E имеет постоянное значение, что позволит в (1.6) вынести E за знак интеграла. Рассмотрим пример применения теоремы Гаусса.

Поле равномерно заряженной плоскости. Пусть относительно прямо-

угольной системы координат бесконечно протяженная плоскость расположена так, что нормаль к плоскости параллельна оси х (рис. 1.4). На плоскости равномерно распределен заряд с поверхностной плотностью . Вектор E в этой задаче может иметь единственное направление – параллельно оси х. В противном случае, существуют отличные от нуля компоненты Ey и Ez. А это противоречит соображениям симметрии: для бесконечной плоскости существует единственное выделенное направление – направление, совпадающее с нормалью к поверхности.

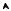z

y

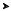x

Построим прямой цилиндр радиуса R, пересекающий заряженную плоскости так, что ось цилиндра совпадает с осью х, а его основания находятся на одинаковом расстоянии от плоскости. Относительно линий вектора E теперь можно сказать, что они параллельны образующим цилиндра и перпендикулярны его основаниям. Будем искать поток вектора E через замкнутую поверхность S цилиндра. Для этого запишем S как сумму боковой поверхно-

Рис. 1.4. К расчету поля заряженной плоскости

сти цилиндра и двух оснований:

		S Sбок 2Sосн			(1.7)
Для потока Ф будем иметь
EdS			EdS 2	EdS.	(1.8)
		Sбок		Sбок

Нормаль к Sбок совпадает с радиусом цилиндра, и угол между этой нормалью и E равен 90 . Нормаль к Sосн совпадает с осью х и направлена вправо, справа от плоскости, и влево, слева от плоскости. Угол нормалей к Sосн составляет с

соответствующим вектором E ноль градусов. С учетом сказанного (1.8) примет значение:

EdS cos 90 2

EdS cos 0 0 2

EdS.

(1.9)

Sбок

Sбок

Sбок

Вектор E по площадке Sосн имеет постоянное значение, так как плоскость

бесконечная, тогда

2E dS 2E R2 .

(1.10)

Sосн

По теореме Гаусса

2E R

2

qвнутр

R2

.

(1.11)

0

0

Отсюда

E

.

(1.12)

2 0

Итак, поле бесконечной равномерно заряженной плоскости не зависит от координат х, у, z, т. е. является однородным. Полученный результат приближенно справедлив и для области, прилегающей к средней части конечной равномерно заряженной плоской поверхности вдали от ее краев.

Уравнение (1.6) называют интегральной формой теоремы Гаусса. Локальная дифференциальная форма записи теоремы Гаусса устанавливает связь между объемной плотностью заряда и изменениями напряженности

E в окрестности данной точки пространства. В декартовой системе координат локальная теорема Гаусса записывается соотношением

Ex Ey Ez / 0 . (1.13)

x y z

Более короткая запись уравнения (1.13) имеет вид
div E / 0	(1.14)

и читается так: дивергенция (расходимость) вектора E в данной точке равна плотности заряда в этой точке, деленной на электрическую постоянную. С помощью векторного дифференциального оператора (набла), определенного как

i x j y k z ,

где i , j, k – орты осей х, у, z, запись дифференциальной формы теоремы Гаусса принимает вид

E / .

(1.15)

Из механики известно, что в поле центральных сил, где F ~ r12 (напри-

мер, гравитационное поле), работа сил поля по произвольному замкнутому пути равна нулю. Математически это можно записать так:

где dl	Fdl 0	,	(1.16)
	– вектор элементарного перемещения.	Поля, обладающие таким свой-

ством, называют потенциальными. Электростатическое поле также является полем центральных сил ( E ~ r12 ) и для него будет иметь место соотношение

(1.16). Поэтому интеграл (1.16) по замкнутому контуру называют циркуляцией вектора F . Можно сказать, что циркуляция вектора E в любом электростатическом поле равна нулю:

Edl 0.

(1.17)

Это утверждение называется теоремой о циркуляции вектора E . Любое электростатическое поле является потенциальным. Из формулы (1.17) сле-

дует, что в электростатическом поле работа по перемещению единицы положительного заряда из точки 1 в точку 2 не зависит от формы пути. Таким образом, можно утверждать, что в электрическом поле существует некоторая скалярная функция координат (r ) , уменьшение которой

2
1 2 Edl ,	(1.18)

1

где 1 и 2 – значения функции в точках 1 и 2. Функция (r ) называется

потенциалом поля.

Потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля. Принято считать,

что потенциал при r равен нулю. Потенциал поля и напряженность поля являются характеристиками одного и того же объекта, следовательно, между ними должна существовать связь. Рассмотрим выражение (1.18) при условии,

что расстояние между точками 1 и 2 равно бесконечно малой величине dl , тогда

1 2 d Edl .

В декартовой системе координат соотношение (1.19) примет вид

E		x	i		y	j		z	k .

(1.19)

(1.20)

Рис. 1.5. Взаимное расположение силовых линий и линий равного потенциала:

Величина, стоящая в скобках, называется градиентом потенциала и обозначается как grad или . В новых обозначениях запись уравнения (1.20) принимает вид

E grad ,	E .	(1.21)
Найдем дивергенцию обеих частей второго из уравнений (21):
E ( ).		(1.22)

С учетом выражения (1.15) получим дифференциальное уравнение, которому должна удовлетворять функция – потенциал:

			2 / 0 .							(1.23)
	Уравнение (1.23) – это уравнение Пуассона, в нем 2 – оператор Лапла-
	са, в декартовых координатах имеющий вид
	2		2		2			2	.	(1.24)
			x2		y2		z 2

Если между заряженными проводниками нет зарядов ( = 0), то уравнение (1.23) переходит в уравнение Лапласа:

2 0 .

(1.25)

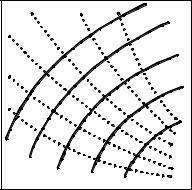
Визуальную картину распределения энергии единичного положительного заряда в электростатическом поле можно получить, построив поверхности равного потенциала – эквипотенциальные поверхности. Покажем, что линии вектора E направлены в каждой точке по нормали к эквипотенциальной поверхности в сторону уменьшения потенциала .

Эквипотенциальные поверхности обычно проводят так, чтобы разность потенциалов для двух соседних поверхностей была одинаковой. Тогда по густоте эквипотенциальных поверхностей можно судить о значении напряженности поля в разных точках. Напряженность поля будет больше там, где поверхности равного потенциала

расположены гуще. Вектор E всюду

нормален к эквипотенциальной по- –– – линии поля E ; - - – = const верхности. На рис. 1.5 показана двумерная картина электрического поля, пунктиром обозначены эквипотенциали, сплошными линиями – линии поля

E .

Ортогональность силовых линий и поверхностей равного потенциала существенно облегчает как экспериментальное, так и теоретическое исследо-

вание электростатического поля. Действительно, если определено семейство одних линий (или поверхностей), то легко решается задача отыскания другого семейства, соответствующего найденному.

Вещества в электрическом поле. При внесении любого вещества в электрическое поле на заряды в веществе (ядра, электроны) начинает действовать кулоновская сила, в результате чего происходит частичное разделение положительных и отрицательных зарядов. Это явление называют электростатической индукцией, а появившиеся нескомпенсированные заряды – индуцированными. Эти заряды также создадут электрическое поле, и в результате поле в веществе будет суперпозицией электрического поля в отсутствии вещества и поля индуцированных зарядов.

Поместим в электростатическое поле металлический проводник. Электроны металла обладают определенной подвижностью, поэтому они придут в движение, в результате чего потенциалы всех точек проводника примут одно значение, и, следовательно, grad станет равным нулю, а поле E внутри проводника по уравнению (1.21) также обратится в нуль.

Любой проводник в электростатическом поле представляет собой эквипотенциальную поверхность. Из этого следует, что непосредственно у этой поверхности поле E направлено по нормали к ней в каждой точке. При помещении во внешнее электростатическое поле диэлектрика, в последнем возникнет поле E , которое будет определяться суммой сторонних электрических зарядов и связанных зарядов вещества диэлектрика. Для удобства описания внутреннего поля вводят вспомогательный вектор D , который зависит только от сторонних зарядов и связан с внутренним полем E соотношением

D 0 E,

(1.26)

где – диэлектрическая проницаемость вещества. Вектор D иногда называ-

ют электрическим смещением или электрической индукцией. Поле вектора D

наглядно можно изобразить с помощью линий вектора D , аналогично линиям вектора E . Линии вектора D могут начинаться и заканчиваться только на сторонних зарядах. Для вектора D теорема Гаусса имеет вид

DdS qвнутр .

(1.27)

Дифференциальная форма теоремы (1.29):

D ,

(1.28)

т. е. дивергенция поля вектора D равна объемной плотности стороннего за-

ряда в той же точке.

Условия на границе. Рассмотрим поведение векторов E и D на гра-

нице раздела двух однородных изотропных диэлектриков с диэлектрическими проницаемостями 1 и 2. Для простоты положим, что на границе раздела сторонних зарядов нет. Обозначим вектор E в первой среде через E 1, а во второй среде – через E 2 и разложим эти векторы на компоненты, параллельные Е и перпендикулярные Еn поверхности раздела. Аналогично разложим и векторы D . Применение теоремы о циркуляции вектора E дает условие на границе раздела сред

E1 E2 .				(1.29)
Применяя теорему Гаусса для вектора D , получим
D1n D2n .				(1.30)
Из условий (1.26), (1.29) и (1.30) следует, что линии векторов		и		на гра-
	E		D
нице раздела преломляются. Выразив в (1.30) электрическое смещение D че-
рез напряженность поля E , получим
1E1n 2 E2n .				(1.31)

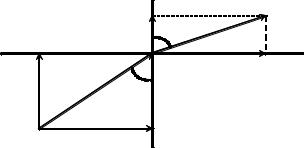
По равенству (1.31) найдем соотношение для углов 1 и 2 (рис. 1.6), определяющих закон преломления вектора E на границе раздела двух сред:

tg 2			E2	/ E2n	2 .	(1.32)
tg	1		E	/ E
			1	1n	1

2		E 2	n	2	E2
1	E1	1			E2
E 1n

E1

Рис. 1.6. Закон преломления E на границе раздела сред

Условие (1.32) означает, что в диэлектрике с бóльшим значением линии E будут составлять бóльший угол с нормалью к границе раздела (на