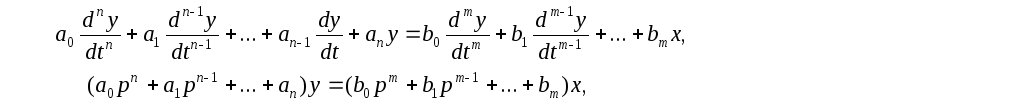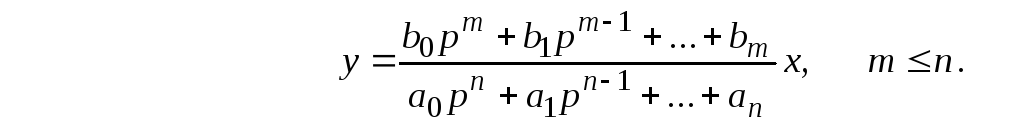Федеральное агентство морского и речного транспорта

Федеральное государственное образовательное учреждение

высшего профессионального образования

Волжская государственная академия водного транспорта

Кафедра информатики, систем управления

и телекоммуникаций

А.В.Преображенский

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Задания на выполнение курсовых работ для студентов очного и заочного обучения по специальности «Эксплуатация судового электрооборудования и средств автоматики»

Нижний Новгород

Издательство ФГОУ ВПО «ВГАВТ»

2010

УДК 681.5

Преображенский А.В.

Теория автоматического управления. Задания на выполнение курсовых работ/ А.В.Преображенский. - Н.Новгород: Изд-во ФГОУ ВПО «ВГАВТ», 2010. - 35 с.

Приведены задания и методические указания по выполнению курсовой работы по теории автоматического управления для студентов очного и заочного обучения по специальности «Эксплуатация судового электрооборудования и средств автоматики».

Компьютерное моделирование динамики системы автоматического регулирования, предусмотренное в заданиях для студентов очного обучения, можно провести в лаборатории автоматики, используя пакет Matlab - Simulink.

Рекомендовано к изданию кафедрой информатики, систем управления и телекоммуникаций (протокол № 4 от 4.03. 2010 г.)

Введение

Курсовая работа выполняется по индивидуальному заданию, отличающемуся видом рассматриваемой системы и численными значениями ее параметров. Номер задания определяется по двум последним цифрам номера зачетной книжки.

В работе предлагается рассмотреть линейную математическую модель системы регулирования, представленную в виде структурной схемы, и оценить параметры регулятора, обеспечивающего удовлетворительное качество управления. Предполагается, что студент знаком с основными понятиями теории автоматического управления. Напомним некоторые из них.

Структурная схема представляет систему регулирования в виде соединения элементов, описываемых передаточными функциями. Передаточная функция – это оператор преобразования входной величины элемента (или системы) в выходную величину. Для получения передаточной функции дифференциальное уравнение, описывающее динамику элемента, представляют в операторной форме, сделав замену d/dt = p:

обычная форма уравнения операторная форма

(1)

где y - выходная величина, х₁ и х₂ – входные величины. Затем, выразив из (1) выходную величину «y», записывают уравнение в «нормализованной» операторной форме:

(2)

где W₁ и W₂ – передаточные функции, определяющие зависимость выходной величины y от каждой входной величины (х₁, х₂) по отдельности. Уравнению (2) соответствует структурная схема элемента, показанная на рис.1. Соединяя соответствующие входы и выходы элементов, получают структурную схему всей системы.

В системах регулирования, работающих по принципу управления по отклонению, элементы системы образуют замкнутый контур. Любая переменная в контуре может рассматриваться и как входная, и как выходная величина. Пример структурной схемы приведен на рис.2.

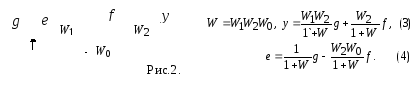
Формулы (3, 4) устанавливают зависимость регулируемой переменной (y) и ошибки регулирования (e) от задающего (g) и возмущающего (f) воздействий. Эти формулы составляются по следующему правилу. Передаточная функция «замкнутой» системы с отрицательной обратной связью, устанавливающая зависимость «выходной» величины от «входной» величины, есть дробь, числитель которой – произведение передаточных функций звеньев, составляющих цепь от «входа» до «выхода» по направлению передачи сигнала, знаменатель – единица плюс передаточная функция разомкнутой системы. Передаточной функцией разомкнутой системы называют произведение передаточных функций всех звеньев, составляющих контур управления, включая звено обратной связи. В рассматриваемом примере это функция W = W₁W₂W₀.

При преобразованиях структурной схемы используют правила, показанные на рис.3.

В общем случае динамика линейной системы описывается дифференциальным уравнением в обычной (5) или операторной (6) форме:

(5) (6)

где x(t) y(t) – отклонения входной и выходной величин от их номинальных значений, соответствующих состоянию равновесия системы. Уравнению (6) соответствует передаточная функция

(7)

При отсутствии внешних воздействий (х = 0) и ненулевых начальных условиях в системе происходит «собственное» движение, являющееся решением дифференциального уравнения

(8)

Первым требованием к системе регулирования является ее устойчивость, т.е. способность возвращаться в состояние равновесия после снятия внешних воздействий. В устойчивой системе собственное движение затухающее, колебательное или апериодическое. Вид собственного движения зависит от корней характеристического уравнения (9):

(9)

Система устойчива, если все действительные корни уравнения (9) отрицательны, а все комплексные корни имеют отрицательные действительные части. При комплексных корнях собственное движение имеет колебательную составляющую.

Динамика системы, показанной на рис. 2, описывается уравнением (3), которое можно представить в форме (10):

(10)

Уравнение собственного движения

.

(11)

Т.к. передаточная функция является отношением многочленов относительно р: W(p)=K(p)/D(p), то характеристическое уравнение 1+W(p) = 0 эквивалентно уравнению D(p)+K(p) = 0. Следовательно, характеристическое уравнение замкнутой системы можно получить, приравняв к 0 сумму числителя и знаменателя передаточной функции разомкнутой системы.

Устойчивость системы можно исследовать, используя критерий Рауса-Гурвица. Согласно этому критерию, система устойчива, если все коэффициенты характеристического уравнения (9) строго положительны (нулевые коэффициенты не допустимы) и выполняются следующие условия:

- для системы третьего порядка	a1a2 – a0a3 > 0 ,	(12)
- для системы четвертого порядка	a3(a1a2 – a0a3) – a4a1^2 > 0	(13)

(системы более высокого порядка при выполнении курсовой работы не рассматриваются).

В качестве примера получим условие устойчивости системы, показанной на рис.4. Характеристическое уравнение

Условие устойчивости

Неравенство (14) определяет границу устойчивости по параметру k. Для того, чтобы качество регулирования было высоким, необходим «запас» устойчивости: параметры системы должны выбираться достаточно далеко от границы устойчивости.

Качество регулирования оценивают по виду переходной характеристики: реакции системы на ступенчатое входное воздействие, задающее (g) и возмущающее (f). По этой характеристике определяют длительность переходного процесса (t_p), перерегулирование (σ), или максимальную динамическую ошибку (δ), статическую ошибку (ε_ст) – см. рис. 5.

Качество регулирования можно оценить теоретически по корням характеристического уравнения. Грубую оценку качества можно получить, пренебрегая малыми постоянными времени инерционных элементов системы и уменьшив порядок характеристического уравнения до второго. В системе, показанной на рис. 4, такое упрощение возможно, еслиT₁<<T. При T₁ = 0, получим характеристическое уравнение Если дискриминант уравнения отрицательный, корниp_1,2 комплексно-сопряженные, собственное движение y(t) колебательное:

Значения С, φ зависят от начальных условий.

Качество переходного процесса системы второго порядка можно оценить по значениям постоянной времени (T_э) и коэффициента затухания (ξ_э). Их находят, приведя характеристическое уравнение общего вида (15) к эквивалентной стандартной форме характеристического уравнения колебательного звена (16):

	(15)	,	(16)

Длительность переходного процесса (при ξ_э < 1) t_р≈ 3T_э/ ξ_э, период колебаний Т_кол≈ 2πТ_э, зависимость перерегулирования σ (в процентах) от ξ_э приведена в таблице 1.

Т а б л и ц а 1

	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
,%	85	72	52	37	25	16	9,5	4,6	1,5	0,2

Чтобы определить статическую ошибку системы регулирования, записывают передаточную функцию, устанавливающую зависимость ошибки (е) от внешнего воздействия, задающего (g) или возмущающего (f), см. рис.2, и делают подстановку р = 0.