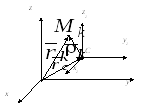Теорема о движении центра масс

Теореме об изменении количества движения в дифференциальной форме можно придать другую формулировку. Учитывая, что , получим

.

Следовательно,

(13.7)

где М – масса всей системы, - ускорение центра масс системы.

Равенство (13.7) выражает теорему о движении центра масс: центр масс механической системы движется также, как двигалась бы материальная точка, в которой сосредоточена масса всей системы под действием силы, равной главному вектору внешних сил системы.

Проектируя равенство (13.7) на оси координат, получим дифференциальные уравнения движения центра масс механической системы:

. (13.8)

Для абсолютно твердых тел уравнения (13.8) являются уравнениями поступательного движения, определяя движение всех точек тела, которые как известно, при поступательном движении движутся одинаково.

Из этой теоремы также вытекает несколько следствий:

1). Одними внутренними силами непосредственно нельзя изменить характер движения центра масс системы

2). Если главный вектор внешних сил на рассматриваемом промежутке времени равен нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно, т.е.,

если то

где - начальная скорость центра масс.

3). Если проекция главного вектора всех внешних сил системы на рассматриваемом промежутке времени на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется, т.е.,

если то.

4). Если известно, что твердое тело движется поступательно, то его движение полностью определяется движением его центра масс.

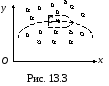
Пример. Рассмотрим движение снаряда под действием силы тяжести, пренебрегая сопротивлением воздуха (рис. 13.3).

Применим теорему о движении центра масс. Внешней силой является только сила тяжести: где М – масса снаряда. Представим, что снаряд взрывается в воздухе (за счет внутренних сил). Будем иметь механическую систему, состоящую

из осколков, массой каждый (k=1,2,…n). Внешними силами будут являться силы тяжести осколков. Применим также теорему о движении центра масс:

.

Получили такое же уравнение. Следовательно, центр масс осколков будет двигаться так же, как если бы снаряд не разорвался.

Вторая мера движения — главный момент количества движения механической системы (кинетический момент)

Рис. 13.4

Моментом количества движения материальной точки относительно центра O называется вектор (рис.13.4), определяемый равенством: , где - скорость точки Мk относительно инерциальной системы отсчета.

Кинетическим моментом (главным моментом количества движения) механической системы относительно центра O называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек, входящих в систему, относительно того же центра:

(13.9)

Кинетический момент абсолютно твёрдого тела относительно точки О соответственно равен

,

где интеграл берётся по массе всего тела (записан условно).

Вычислим кинетический момент механической системы, участвующей в сложном движение.

Рис. 13.5

Пусть Охyz – инерциальная система отсчёта. За подвижную систему координат примем систему координат Cx2y2z2 c началом в центре масс механической системы и движущуюся поступательно относительно системы координат Oxyz. Такая система координат называется кёнинговой системой координат.

Положение произвольной точки M_k (k = 1, 2,..., n) механической системы относительно центра О определим радиус-вектором , относительно центра масс - радиус-вектором . Положение центра масс относительно центра О определим радиус-вектором (рис. 13.5). Тогда . По определению центра масс , где -масса всей системы. Откуда .

Рассмотрим движение точки М_k как сложное, состоящее из переносного движения со скоростью и относительного движения со скоростью. Следовательно, по теореме сложения скоростей абсолютная скорость точкиМ_k равна

Учитывая, что так как за переносное движение приняли поступательное движение осейСх₂у₂z₂ вместе с центром масс, получим

Тогда по определению

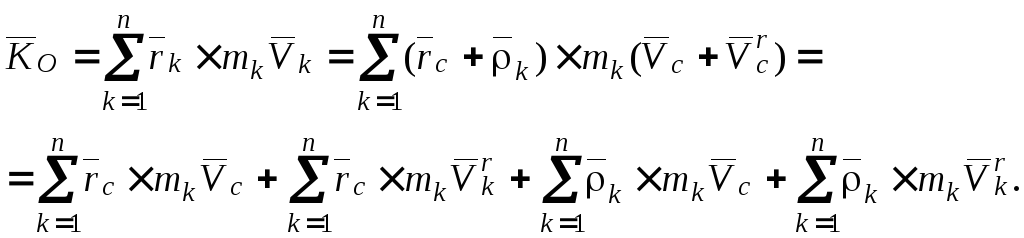
Обозначим в последнем равенстве первое слагаемое - , второе слагаемое -, третье слагаемое - и четвёртое слагаемое -. Преобразуем по отдельности первые три слагаемых, учитывая, что векторы , и, не зависят от индекса суммированияk и их можно вынести за знак суммы:

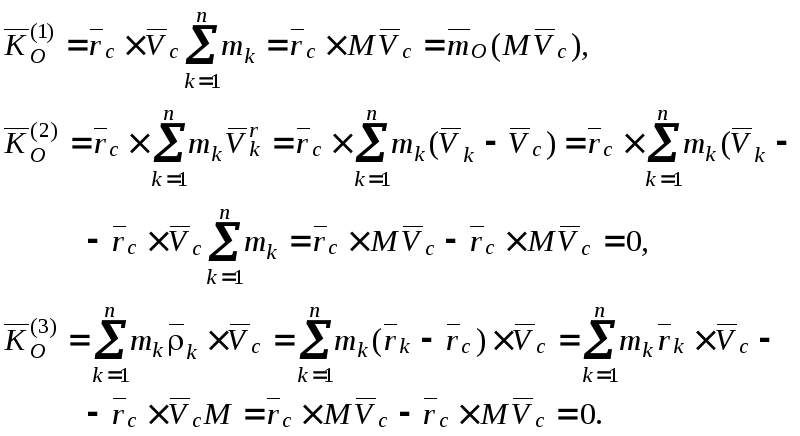
Тогда получим

(13.10)

Следовательно, если механическая система совершает сложное движение, то её кинетический момент относительно неподвижного центра О равен геометрической сумме момента количества движения центра масс так как если бы в нём была сосредоточена масса всей системы и кинетического момента механической системы в её относительном движении вокруг центра масс.