Karmanov_Trojanov

Сформируем массивы для представления схемы уровней и постро-
им волновые функции для первых пяти состояний:
m := 0 .. 1	j :=	0 .. 14	Elevelm, j := eLj		Xe0, j := 0		Xe1, j := XN
		20
ψ(x,eL0,A0) 10
ψ(x,eL1,A1)
ψ(x,eL2,A2)
ψ(x,eL3,A3)		0
ψ(x,eL4,A4)
Ugr
Elevel		10
		20
			0	5	10	15	20
				x,x,x,x,x,Xgr ,Xe
	Рис. 3. Уровни энергии системы и ненормированные
	волновые функции пяти низколежащих состояний
Можно ожидать, что при увеличении количества потенциальных ям в
системе будет формироваться структура, близкая к зонной структуре
одномерного кристалла.

10

Редукция системы уравнений

Волновую функцию частицы в кусочно постоянном потенциале можно представить с помощью двух матриц: вектора-строки плоских волн и вектора-столбца коэффициентов [6]:

ψ(x) = A exp(i k x) + B exp(−i k x) = (ei k x e− i k x )	A .
	B

Тогда условия непрерывности волновой функции и ее первой производной, например, на левой границе области (при x = 0) можно записать в виде

A0 + B0 = A1 + B1 k0 (A0 − B0) = k1 (A1 − B1)

Разрешая эту систему уравнений относительно A1 и B1, находим в явном виде матрицу скачка потенциала от U0 (слева) до U1 (справа):

		A							A
				1			= D				0
		B		1				01	B		0
							k			k
							0			0
			1		+ k			1 − k
D = 1
						1				1
01	2						k0			k0
			1		−			1 +
							k			k
						1				1

Переходя к следующей точке разрыва потенциала, получаем систему двух уравнений такого же вида, если учесть, что фазовые множители exp( ±i kna) уже включены в коэффициенты A1, B1, A2 и B2 посред-

ством соотношений,связывающих эти коэффициенты на краях участка постоянства потенциала.

A2 e

i k2 a

A1 e

i k1 a

= D

B

e

− i k2 a

12

B

e

− i k1 a

2

1

11

												k				k
													1			1
										1	+ k			1 −		k
					D			= 1					2		2
						12		2				k1				k1
										1	−			1 +
												k				k
													2		2
	A e				i k1 a				i k1 a						A
														0
		1						e											1
			e	− i k a			=				e		− i k a			B			1
B		1			1			0						1
	A e				i k2 a				i k2 a						A
														0
		2						e											2
			e	− i k a			=				e		− i k a			B			2
B		2			2			0						2

=P1 A1

B1

=P2 A2

B2

Входящую сюда матрицу P(x) будем называть матрицей распространения волновой функции на расстояние x в поле ступеньки U1,2 ,

а матрицу D12 – матрицей скачка потенциала от U1 до U2 . Выражая исходные коэффициенты A2 и B2 через A1 и B1 , имеем базовое соотношение

A				− 1	A
	2		= (P(a)2)			1	,
B					D12 P(a)1 B
	2					1

определяющее матрицу перехода от одной точки разрыва потенциала к следующей

T(a)2 = (P(a)2)− 1 D12 P(a)1 .

Примение этого соотношения к следующим участкам постоянства потенциала позволяет провести редукцию исходной системы линейных уравнений для коэффициентов волновой функции к цепочке линейных уравнений с матрицами второго порядка.

A				− 1		A
	n+1		= (P(Xn)n+1)		Dn,n+1 P(Xn)n		n
B	n+1					B	n

12

Здесь X ,U	– массивы, задающие распределение потенциала.
n n

Матрицы распространения и скачка потенциала имеют вид.

e

i kn+1 Xn

0

P(Xn)n+1 =

0

e

− i kn+1 Xn

k

k

n

n

1

+ k

1 − k

1

D

=

n+1

n+1

n,n+1

2

kn

kn

1

−

1 +

k

k

n+1

n+1

Отметим, что все волновые числа, входящие в определение матриц, стандартным образом зависят от энергии E и от потенциала U:

	2 mc2 (E − Un)			,			.
kn =		hc			0	≤ n ≤ N + 1
В случае δ – потенциала		вида	U(x) = α δ(x)			система уравнений
для связи коэффициентов		волновой функции по обе стороны от

барьера будет состоять из условия непрерывности функции и соотношения для скачка производной:

A2 + B2 = A1 + B1

i k (A2 − B2) − i k (A1 − B1) =

2 m α

(A1 + B1)

2

h

Отсюда получаем матрицу δ – потенциала

1

−

i m α −i m α

Del(α)

k h2

k h2

=

i m α

i m α

1 +

2

2

k h

k h

13

Матрицы и их свойства

Введенные выше матрицы обладают следующими свойствами [6]. 1) Матрицы распространения частицы в постоянном потенциале:

	a)	P(0) =	1	0	= P(r) P(−r) = I	;
			0	1

b)P(r1)P(r2) = P(r1 + r2)= P(r2) P(r1) ;

с)	P A = A P	если					−			,
			exp(i k a)			= exp( i		k a)
в этом случае			π и	P = I		или	P =		− .
	k a = n								I
2) Матрицы скачка потенциала:
a)	D12 D21 =	D11 = I =		1	0	;
				0	1

b)D12 D23 = D13 ;

с)	D12 D23 = D23 D12 ,

3) Матрицы δ – потенциала:

a)	Del(α) Del(−α) = I =		1	0	;
			0	1
b)	Del(α) = lim	(D21 P(a) D12)
	a →	0
	при условии, что при		U2 –> ∞
	alim→ 0 a (U2	− U1)	= α .

Используя свойства матрицы распространения, можно показать,что

P(Xn)n (P(Xn−1)n)− 1 = P(∆Xn)n = exp(i kn∆Xn)

0

где	∆X = X		− X	, ∆X = 0 ,
	n	n	n−1	0

0

exp(−i kn∆Xn) 0 ≤ n ≤ N

14

Основное уравнение

Коэффициенты волновой функции на произвольном участке постоянства потенциала связаны с коэффициентами на левой границе области следующим соотношением:

A				− 1	0	A
	n+1		= (P(Xn)n+1)		∏		0
B	n+1					(Dj, j+1 P(∆Xj)j) B	0		.
					j = n

При n = N эта связь с учетом граничных условий слева (A0 = 0) и справа (BN+1 = 0) имеет вид

AN+1

− i kN+1 XN

0

T

0,0

T

0

,1

0

e

=

0

e

i k

X

T

1,0

T

1

,1

B

0

0

N+1

N

или

AN+1 = T(E)0,1 B0 exp(−i kN+1 XN)

0 = T(E)1,1 B0 exp(i kN+1 XN)

Входящую сюда матрицу T будем называть матрицей перехода для системы:

0

T = ∏ (Dj, j+1 P(∆Xj)j) . j = N

Решение системы уравнений для коэффициентов волновой функции связанного состояния существует, если

T(E)1,1 = 0 ,

а это и есть уравнение для определения уровней энергии. После того,

как уровни энергии найдены, коэффициенты An , Bn ненормированной волновой функции (A0 = 0 , B0 = 1) могут быть найдены с помощью рекурентного соотношения

A				− 1	A
	n+1					n	.
B			= (P(Xn)n+1)		Dn,n+1 P(Xn)n B
	n+1					n

15

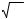
Одномерная потенциальная решетка с дефектом

Рассмотрим одномерную решетку, состоящую из N0 =10–15 атомов.

Каждому атому соответствует прямоугольная потенциальная яма. Все ямы отделены друг от друга равновысокими барьерами. Предположим, что в подобной одномерной системе одиниз атомов является нестандартным (примесь). Потенциальная яма, соответствующая данному атому, имеет ширину, большую или меньшую ширины потенциальных ям атомов решетки. Рассчитаем спектр энергий в такой системе и волновые функции нескольких состояний атома-примеси.

mc2 := 0.511 106 eV	hc := 1.9732858 103	eV A	i := −1
No := 11 число атомов	N := 2 No − 1	число узлов Xn -1

Пусть стандартные ямы имеют следующие параметры:

a := 3.5 A				Ua := 25 eV		b := 0.5 A	Ub := 26.5 eV
K := 6				ak := 3.3	A	номер и размер дефектной ямы
Uo :=		max(Ua,Ub)			ad( j) := if ( j = 2 K − 1,ak,a)
U :=		au0 ← 0
		for		j 1 .. N
				auj ← (−Ua)	if (mod( j,2) = 1)
				auj ← 0 otherwise
				auj ← −Ub if j = 2 K − 1
		auN+1 ← 0
		au
X :=		ab0 ← 0
		for		j 1 .. N
				abj ← (abj−1 + ad( j))		if (mod( j,2) = 1)
				abj ← (abj−1 + b) otherwise
		ab

16

Сформируем массивы для графика потенциала

Ugr :=

Au0 ← U0

Xgr :=

for

j 0 .. N

for j 1 .. N

ax2 j ← Xj

j2 ← 2 j − 1

ax2 j+1 ← Xj

Auj2 ← Uj

ax

Auj2+1 ← Uj

Au2 N+1 ← UN+1

Au

0

Ugr

20

0

10

20

30

40

Xgr

Рис. 4. Потенциальная решетка с дефектом

Определим волновые числа для разных областей потенциала, сформируем матрицы скачков потенциала и матрицы распространения и после этого определяем матрицу перехода. Пусть

	k1(e) :=	2 mc2 e	k2(e, j) :=		2 mc2 (e − Uj)
		hc			hc
		k(e, j) := if (mod( j,2) = 0,k1(e) ,k2(e, j))
	dX0 := 0		n := 1 .. N	dXn := Xn − Xn−1

17

P(e, j,x) :=		exp(i k(e, j) x)
					0
			1	+	k(e, j)
	1				k(e, j + 1)
D(e, j) :=
	2				k(e, j)
			1	−
					k(e, j + 1)

0 exp(−i k(e, j) x)

	1 −	k(e, j)
		k(e, j +	1)
	1 +	k(e, j)
		k(e, j +	1)

Матрица перехода для всей системы равна произведению матриц скачка и распространения на примыкающем к нему слева участке постоянства потенциала:

0

T(e) := ∏ D(e, j) P(e, j,dXj) , j = N

тогда уравнение для определения корней имеет вид

T(e)1,1 = 0 .

Для поиска положения корней воспользуемся функцией

En(ff ,En,Em,de) := n ← 0 E ← En

D1 ← ff(E) while E < Em

E ← E + de D2 ← ff(E)

if (D1 D2 < 0)

Aen ← E − de n ← n + 1

D1 ← D2

Ae

18

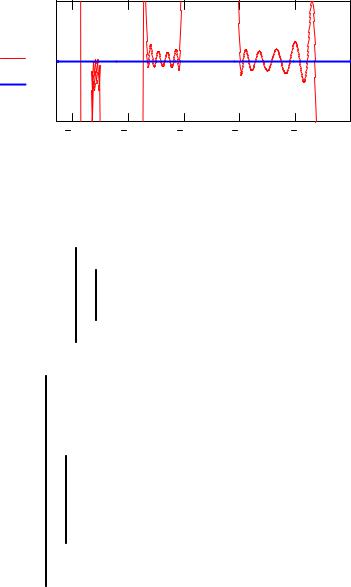
Пусть	f(e) := T(e)	1,1	e := −0.999 Uo,−0.998 Uo .. −0.01
f(e)
0	0
	25	20	15	10	5	0
				e
Рис. 5.	К определению положения уровней в решетке с дефектом

Вычисляем начальные значения корней и затем уточняем их с помощью встроенной функции root(..).

EA := En(f,−0.999 Uo,−0.02,0.001) Nlev := rows(EA) Nlev = 33
El(nlev,Ea) := for n 0 .. nlev − 1
E ← Ean
ELn ← root(f(E) ,E)	eL := El(Nlev,EA)

EL

Коэффициенты волновой функции для выбранной энергии:

AB(e) := A0 ← 0

B0 ← 1

for n 0 .. N

Tn ← (P(e,n + 1,Xn))− 1 D(e,n) P(e,n,Xn)

An+1 ← Tn AnBn+1 Bn

A

B

19