ТВиМС.Малярец.Егоршин 22.12.12

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

Малярец Л. М.

Егоршин А. А.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Учебное пособие для студентов отрасли знаний 0305 «Экономика и предпринимательство»

Харьков, Изд. ХНЭУ, 2012

1

УДК 519.2 (042.4)

ББК 22.17я73 М 21

Рецензенты: докт. физ.-мат. наук, профессор кафедры высшей математики Национального аэрокосмического университета им. М. Е. Жуковского «ХАИ» Проценко В. С.; докт. экон. наук, профессор, заведующий кафедрой математики и математических методов экономики Донецкого национального университета Христиановский В. В.

Рекомендовано к изданию решением учёного совета Харьковского национального экономического университета.

Протокол № от

Малярец Л. М.

М 21. Теория вероятностей и математическая статистика : учебное пособие для студентов отрасли знаний 0305 «Экономика и предпринимательство» / Л. М. Малярец, А.А. Егоршин. – Х. : Изд. ХНЭУ, 2012. – 305 (Русск. яз.)

Изложен теоретический материал по учебной дисциплине, сформированный по лекциям, каждая из которых сопровождается примерами и задачами, вопросами для самопроверки. Разработаны лабораторные работы.

Рекомендовано для всех студентов, которые изучают теорию вероятностей и математическую статистику.

© Харьковский национальный экономический университет, 2012

© Малярец Л. М., Егоршин А.А., 2012

2

Введение

Дисциплина «Теория вероятностей и математическая статистика» много лет преподается преподавателями кафедры высшей математики и экономикоматематических методов студентам всех срециальностей университета. В 70-е годы XX столетия многие преподаватели Харьковского национального экономического университета слушали курс лекций по теории вероятностей и математической статистики у прекрасного специалиста, руководителя Харьковской научной школы математиков-экономистов Воловельской Софьи Натановны. XXI век существенно отличается от прошлого. Появились персональные компьютеры и доступное программное обеспечение. Ушли в прошлое громоздкие ручные вычисления, разрешены многие прикладные проблемы многомерного статистического анализа. Появилось много новых книг и учебников по теории вероятностей. В подавляющем большинстве пособий принят следующий стиль изложения: многословно и высокопарно распространяться по поводу очевидных утверждений и в то же время пропускаются все доказательства. Однако, бесспорным фактом есть, что простые вещи следует излагать просто, приводя все ключевые доказательства или мелким шрифтом, или в виде приложений, или делая ссылку на доступные источники, где имеются эти доказательства, так, как сделано в данном учебном пособии.

Более того, несмотря на требования к строгости изложения, в последнее время окончательно закрепились странные словосочетания типа «сумма событий», «произведение событий», «частотная гистограмма» или, например, определение: «Математическое ожидание – это сумма произведений значений случайной величины на вероятность их появления». Ошибкой, на взгляд авторов, в данном определении есть то, что вместо ответа на вопрос: «Что это такое?» приведено описание вычислительной формулы для частного случая дискретной случайной величины. Поэтому авторы в данном пособии попытались не следовать тенденции сокращенного изложения материала, а изложили материал с объяснениями, исходя из теории и практики применения самих инструментов для решения экономических задач.

В пособии, согласно рабочей программе нормативной дисциплины «Теория вероятностей и математическая статистика», на изучение теории выделяются 17 лекций, 8 лабораторных работ и 8 практических занятий. Отличительной особенностью изложения теории в пособии есть структурирование ее по лекциям, которые содержат весь необходимый материал для приобретения компетенций теоретического содержания инструментов теории вероятностей и

3

математической статистики. Теоретический материал сопровождается многочисленными решенными примерами и задачами, демонстрирующие применение соответствующих теорем, определений, формул.

Впособии, также, изложено 8 лабораторных работ, где детально объясняется их выполнение. Для закрепления материала каждая лекция и каждая лабораторная работа заканыичается вопросами для самопроверки. Кроме этого, в виде справочника написаны разделы «Теория вероятностей в вопросах и ответах», «Математическая статистика в вопросах и ответах», «Регрессионный анализ в вопросах и ответах».

После изучения дисциплины студенты должны уметь: определять вероятности случайных событий,; знать основные теоремы теории вероятностей и математической статистики, их экономическую интерпретацию; применять схемы независимых испытаний для решения экономических задач; знать законы распределения и числовые характеристики одномерных и многомерных случайных величин; иметь представление о теории случайных процессов; уметь первоначально обработать статистические данные; оценивать параметры распределения; проверить ститистические гипотезы, знать элементы дисперсионного анализа, теории корреляции и регрессионного анализа.

Вцелом, изучив материал в пособии, студенты должны приобрести такие компетентности, как: знания фундаментальных основ теории вероятностей и математической статистики, умения использовать данные инструменты для решения реальных задач в экономике, ценности практической реализации методов теории вероятностей и математической статистики в деятельности экономистов, менеджеров, аналитиков.

4

1. Основные понятия теории вероятностей

Основы знаний об окружающем мире у человека закладываются с младенчества. Именно тогда он на практических примерах усваивает основные понятия и формулирует правила поведения, позволяющие ему выжить и избежать большинства неприятностей.

В школе начинается подробное изучение явлений природы, но для удобства усвоения все явления классифицируются по отдельным наукам. Так, выделяют определенный круг вопросов и называют его физикой, другие группы явлений – арифметикой, геометрией и т. д. Теорию вероятностей начинают изучать поздно, чаще всего уже после окончания школы, когда у человека сформировалось критическое мышление. Приступая к изучению нового раздела знаний, учащийся (студент) ожидает, что ему сначала будут даны строгие определения всех новых понятий нового этого раздела науки. И тут оказывается, что основные понятия любой науки только называются, демонстрируются на примерах и устанавливается иерархия соподчинения; строгие же определения отсутствуют. Даже в такой науке, как математика, изначально считаются известными такие понятия, как «точка», «прямая», «плоскость»; определений этих основополагающих понятий нет. Соподчиненность устанавливается фразами типа: «На прямой лежат точки». Учащийся обычно не задает лишних вопросов, ему и так кажется все понятным.

Приведем показательный пример из физики. Ни в одной книге, как в учебной, так и научной, нельзя найти определения температуры, хотя всем как будто бы понятно, что это такое. В каждом терминологическом словаре температура определяется как средняя кинетическая энергия молекул в хаотическом движении. Тут одно непонятное слово «температура» заменено другим непонятным словом «энергия». Положение еще больше запутывается, если учесть, что прибор, который называется термометром, никакую температуру не измеряет, он измеряет изменение объема тел (ртути, спирта, разных металлов) при нагревании.

Теория вероятностей – наука, основные понятия которой только называются и демонстрируются на примерах. По большому счету, они нам уже известны. В некоторых учебниках пытаются дать определения исходных понятий теории вероятностей, но этого не стоит делать: большое количество бесполезных пояснений снижает уровень понимания (то, что было ясным, становится непонятным после многословных объяснений).

5

Известны понятия «испытание», «случайное событие»; далее в пособии появятся «случайная величина» и «случайная функция». Соподчиненность устанавливается фразой: «При испытаниях происходят события». Примеры: при броске монеты («испытание») может выпасть герб («событие Г») или решка («событие Р»); студент пришел на экзамен (на украинском языке «іспит») и получил неудовлетворительную оценку (очень неприятное событие).

Любой взрослый человек, никогда специально не изучавший теорию вероятностей, правильно ответит на вопрос: «Какова вероятность выпадения герба при броске монеты?». Более того, немного подумав, он даже обоснует, почему эта вероятность равна 0,5. Любой человек правильно объяснит разницу между вероятностью выпадения герба (0,5) и вероятностью (0,8) поражения мишени метким стрелком – при повторении испытаний стрелок чаще попадает, чем промахивается, а при броске монеты герб и решка появляются с одинаковой частотой. Можно попросить его сформулировать, что же такое «вероятность», и, в итоге, он ответит, что: вероятность – это число, которое показывает, как часто происходит событие (А) при испытаниях. Это число изменяется в пределах 0 рА 1, или 0 рА 100 % (в процентах). Если рА = 0, событие А является невозможным, невероятным, оно никогда не происходит, сколько бы не повторялись испытания. Если, наоборот, рА = 1, то событие А обязательно произойдет в каждом испытании, иными словами, такое событие не является случайным, его называют детерминированным, достоверным.

Предложено обозначать невозможные события символом		, тогда р	= 0.
Детерминированные события следует обозначать символом		, тогда р	= 1.
Объект	называют еще пространством всех событий и универсумом.		Все

остальные события, для которых 0 < рА < 1, случайные, вероятностные.

Отсюда следует универсальный способ определения (в смысле «вычисления») вероятности – статистическое (или стохастическое) определение вероятности. Испытания производятся n раз и фиксируется, сколько раз при этом появилось событие A; число появления события называется частотой m. Отно-

сительная частота mn (частость) изменяется от 0 до 1 и показывает, как часто

появлялось событие при n испытаниях. Ожидается, что с увеличением числа испытаний это отношение должно приближаться к некому пределу – вероятности события А :

pA	lim	m n	.
	n	n

6

Рис. 1.1. Изображение

несовместных событий

Как правило, эти ожидания оправдываются, например, при испытаниях с бросками монеты, игральной кости и т. п. Однако бывают также неприятные эффекты: при длительных испытаниях изнашивается инструмент, стареет агрегат, улетучиваются легкие фракции, то есть с каждым испытанием изменяются условия проведения опыта. В этих случаях (нарушение однородности) способ статистических испытаний, естественно, не применим.

Иногда возможны иные способы определения вероятностей без проведения длительных испытаний. К ним относятся способ назначения вероятности из геометрических соображений и классический способ вычисления вероятностей, использующие наличие равновероятности некоторых исходов испытания. Оба эти способы будут рассмотрены ниже. Они не являются универсальными и имеют вполне определенную область применения.

Когда невозможен ни один из вышеупомянутых способов, применяют способ экспертных оценок. Группа экспертов обсуждает вероятности неких начальных простых событий, а вероятности более сложных последствий уже рассчитываются на основе известных теорем теории вероятностей.

Кстати, эквивалентными являются названия: «событие», «случайное событие», «случай» («казус»), «исход испытания», «результат опыта».

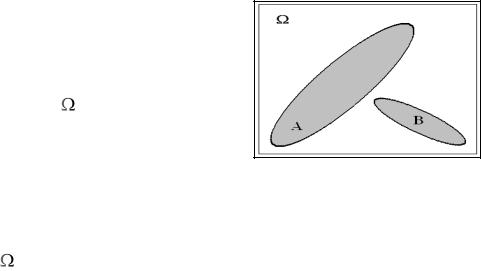
Рассмотрим геометрическое представление событий и геометрический способ определения вероятностей. На рис. 1.1 изображены два события A и B

в виде неких геометрических фигур (диаграмм Венна). Обе фигуры расположены в прямоугольнике, который представляет собой универсум (пространство всех событий, достоверное событие) . Расположение и форма фигур определяются конкретными условиями задачи. Если все точки универсума равновероятны, то площади фигур будут пропорциональны вероятностям изображен-

ных событий. Действительно, представим себе метеорологический столик (прямоугольник ), на котором стоят ванночки А, В. Какова вероятность того, что капли дождя попадут в ванночку А? Поскольку предполагается, что капли дождя падают на столик равномерно, доля капель, попавших в ванночку А, будет пропорциональна только ее площади, но не ее форме и расположению на столике.

7

Рис. 1.2. Область встречи

Если нам удалось построить геометрические изображения событий, то вероятности событий можно получить как отношения площадей изображенных фигур к площади универсума:

p	A	SA	, p	B	SB	.
		S			S

Пример 1. Задача о встрече. Два студента договорились встретиться в определенном месте в период от 1200 до 1300 и ждать друг друга не более четверти часа (15 мин.). Какова вероятность, что встреча состоится?

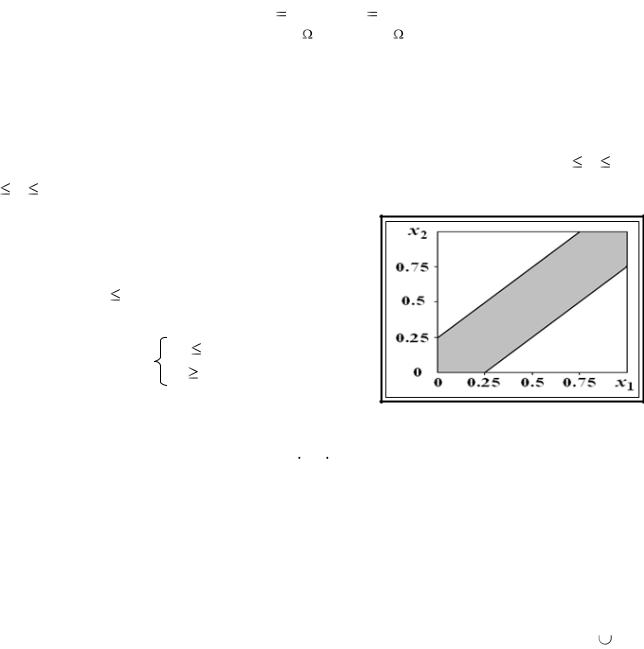
Обозначим через х – время прихода 1-го студента в условленное место, а через у – время прихода 2-го студента. Согласно условиям задачи, 0 х 1, 0 у 1, что геометрически определяет квадрат со стороной 1.

Это универсум, пространство всех равновозможных комбинаций времени прихода студентов на место встречи. Встреча состоится, если | x – y | 0,25. Сформулированное неравенство можно переписать в виде системы:

ух + 0,25

ух – 0,25 ,

которая определяет область, изображенную на рис. 1.2.

Площадь этой области S = 1 – 2 0,5 0,752 = 1 – 0,5625 = 0,4375 равна искомой вероятности, так как площадь универсума (квадрата) равна единице. События, изображенные на рис. 1.2, несовместные, их области не пересекаются.

Несовместные события не могут появиться в одном испытании.

Иногда неважно, какое именно событие (А или В) появится, в обоих случаях получится ожидаемый результат (неважно, в какую именно ванночку попадают капли дождя, далее будет подсчитываться общий объем собранной воды). Нас интересует вероятность события (А или В), которое обозначается A B, или A+B (операция объединения множеств).

Из рис. 1.2 видно, что при вычислении вероятности p(А+В) площади непересекающихся фигур надо складывать. Таким образом, геометрически проиллюстрировано утверждение: «Вероятность появления одного из несовместных событий (любого) равна сумме их вероятностей».

Это утверждение называется аксиомой сложения вероятностей:

P(А+В) = pА + pВ ,

где А, В – несовместные.

8

совместных событий

Рис. 1.3. Изображение

К сожалению, аналогия между логической операцией объединения множеств и арифметической операцией сложения чисел стала причиной появления жаргонной терминологии «сумма событий».

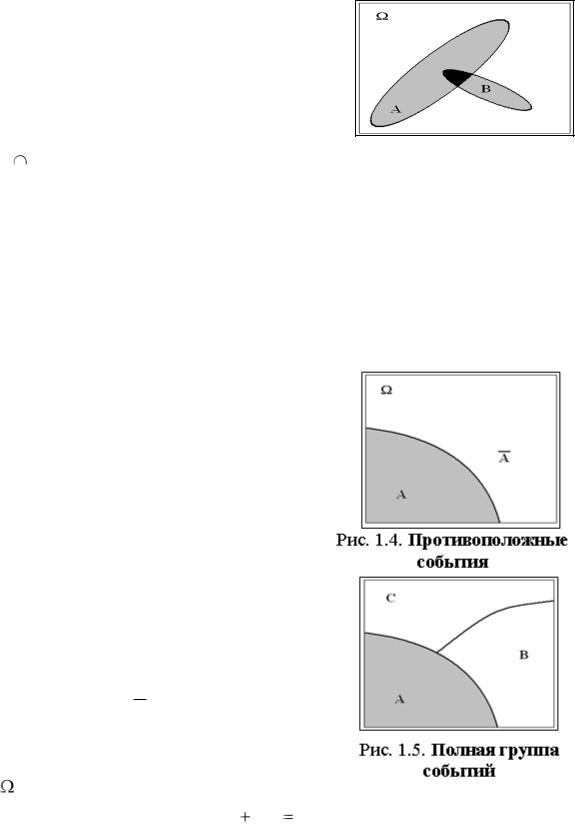
На рис. 1.3 изображены совместные события (их области пересекаются).

Совместные события могут появиться одновременно в одном испытании.

Операция пересечения событий А и В обозначается A B или просто AB (на основе последнего обозначения появилась жаргонная терми-

нология «произведение событий»). На рис. 1.3 произведению соответствует общая зона, принадлежащая одновременно и A, и B. Этот же рисунок позволяет обосновать утверждение: «Вероятность появления одного из событий равна сумме вероятностей этих событий минус вероятность их совместного появления»: P(А+В) = pА + pВ – pАВ . Для несовместных событий A, B pАВ = 0. Это утверждение называется теоремой сложения вероятностей. Действительно, пусть на метереологическом столике ванноч-

ки события A и B расположены на двух уровнях, поэтому одна ванночка перекрывает другую. После испытания вода из обеих ванночек будет учитываться вместе, поэтому неважно, в какую именно ванночку попадают капли дождя. Тогда вероятность того, что капли дождя попадут в ванночки, будет пропорциональна площади общей затушеванной области, которая равна сумме площадей области A и дополнительной части области B без уже учтенной области AB.

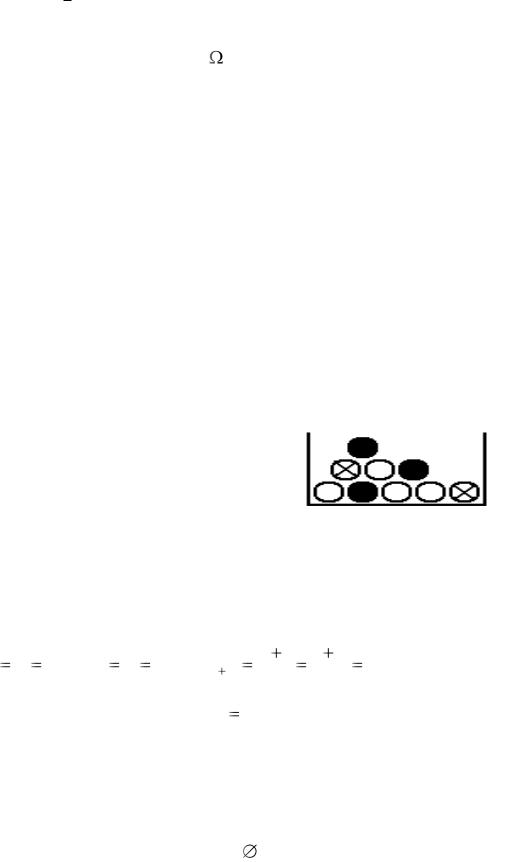
На рис. 1.4, 1.5 изображены противоположные события A и A (не A). Противоположные события образуют полную группу событий – их объединение дает универсум:

A+ A = . Сумма вероятностей			противопо-
ложных событий равна единице:			pA p		1.
				A

9

Рис. 1.6. Урна с

шарами

Для обозначения вероятности противоположных событий часто используется обозначение qA = pA , тогда всегда p + q = 1.

События A, B, C составляют полную группу, если при испытании одно из них обязательно произойдет: (A + B + C) = . Если эти события несовместные, то сумма их вероятностей будет равна единице рА + рВ + рС = 1 (см. рис. 1.5).

Успех в решении многих задач теории вероятностей зависит от умения представить исходы испытания в виде полной группы несовместных событий (этот прием будет подробно рассмотрен в следующих лекциях).

Переходим к изложению так называемого классического способа определения вероятностей. Этот способ имеет достаточно ограниченную область применения. Название «классический способ» закрепилось исторически, поскольку ученые – основоположники теории вероятностей – сначала изучали события, связанные с азартными играми, которые в отличие от жизненных ситуаций имеют специфические особенности – в них все определено заранее. Несмотря на внешнее разнообразие, многие игры можно свести к одной – извлечению шаров из урны.

На рис. 1.6 изображена такая урна, в которой имеется n = 9 шаров, одинаковых по размерам и неразличимых на ощупь. Шары помечены различными признаками, так, среди изоб-

раженных шаров имеется m = 4 белых (A), k = 3 черных (B) и l = 2 синих (C). Шары извлекаются из урны по одному в случайном порядке.

Каковы вероятности извлечь черный, синий и белый шары?

На все эти вопросы даже неподготовленный человек обычно дает правильные ответы:

p

k

3

; p

l

2

; p

k l

3 2

5

.

B

B C

n 9

C

n 9

n

9

9

Фактически используются формула pA

mA

и утверждение, что вероят-

n

ность появления одного из несовместных событий равна сумме вероятностей указанных событий. Однако из этих двух утверждений одно является следствием другого. Строго доказать сразу оба утверждения невозможно, одно из них следует принять за исходный постулат (аксиому). Предлагается принять за аксиому утверждение рА+В = рА + рВ , если АВ = (аксиому сложения вероятностей). На примере убедились в справедливости аксиомы сложения для частного случая геометрической вероятности, она представляется очевидной и для част-

10