динамика / Glava_2d

Глава 2. Динамика относительного движения МТ

2.1. Дифференциальные уравнения

относительного движения МТ

Пусть имеется инерциальная система отсчета О₁x₁y₁z₁. Рассмотрим движение МТ массы m по отношению к неинерциальной системе отсчета Oxyz, которая произвольным образом (с ускорением) движется по отношению к инерциальной системе отсчета (рис. 18).

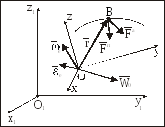
Рис. 18

На основании второго (основного) закона динамики – соотношения (1.2) для несвободной МТ имеем:

, (2.1)

где , – абсолютное ускорение МТ – ускорение МТ по отношению к инерциальной системе координат.

Используя теорему о сложении скоростей в сложном движении МТ (Ч.1 Кинематика), перепишем соотношение (2.1) в виде:

, (2.2)

здесь – относительное ускорение МТ, – переносное ускорение МТ, – ускорение Кориолиса.

Совершив простейшие алгебраические преобразования и введя обозначения сил инерции, получим:

, (2.3)

где – переносная сила инерции,

– сила инерции Кориолиса.

В этих соотношениях использованы формулы (Ч.1 Кинематика) для ускорения точки НМС в общем случае ее движения и формулы для ускорения Кориолиса, в которых – абсолютное ускорение начала неинерциальной системы координат, и – угловые скорость и ускорение неинерциальной системы координат по отношению к инерциальной, и – относительные скорость и ускорения МТ по отношению неинерциальной системы координат.

Из соотношения (2.3) следует, что движение МТ относительно неинерциальной системы отсчета можно рассматривать так же, как и относительно инерциальной, добавляя при этом в правую часть уравнения движения МТ переносную и кориолисову силы инерции.

2.2. Равновесие МТ вблизи поверхности Земли

Для равновесия несвободной МТ, подвешенной на нити, () вблизи поверхности Земли (рис. 19) соотношение (2.3) примет вид:

,

где – сила всемирного тяготения, направленная к центру Земли, – пассивная сила – сила реакции нити, – нормальная составляющая переносной силы инерции вследствие вращения Земли (угловая скорость суточного вращения Земли =const), направленная по кратчайшему расстоянию к оси вращения и равная по модулю (₁ – расстояние МТ от земной оси).

Уравнение равновесия МТ в неинерциальной системе отсчета, связанной с земной поверхностью, будет иметь вид:

. (2.4)

Из соотношения (2.4) следует, что – пассивная сила – сила реакции нити уравновешивается – силой тяжести МТ, являющейся равнодействующей силы всемирного тяготения и переносной силы инерции :

. (2.5)

Линия действия силы тяжести МТ называется вертикалью в данном пункте земной поверхности. Угол , составленный вертикалью (а не радиусом Земли) с плоскостью экватора, называется географической широтой в данном пункте земной поверхности. Так как модуль силы является малой величиной (величина очень мала) по сравнению с модулем силы , то направление силы мало отличается от направления силы .

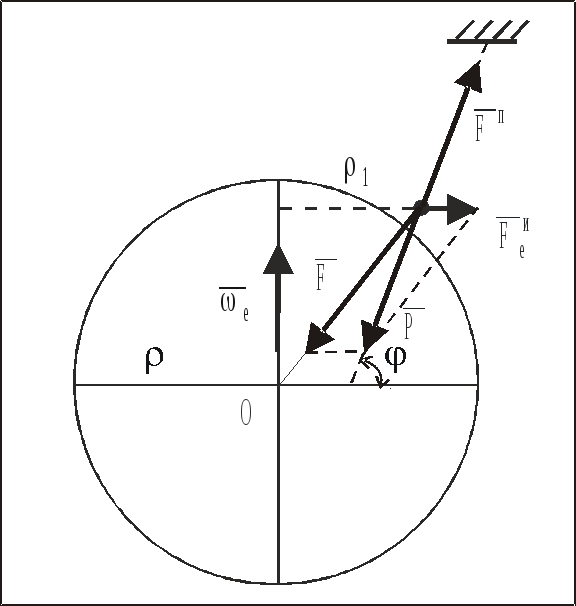
Рис. 19

Так как масса МТ постоянна, то из соотношения (2.5) и второго (основного) закона динамики следует, что сила тяжести и ускорение свободного падения зависят от географической широты в данном пункте земной поверхности. Наибольшее значение сила тяжести , а, следовательно, и – ускорение свободного падения будет иметь на полюсах Земли, а наименьшее – на экваторе.

2.3. Отклонение к востоку МТ,

падающей вблизи поверхности Земли

Рассмотрим МТ, массы m, падающую без начальной скорости на поверхность Земли с малой (по сравнению с радиусом Земли) высоты h, так что – ускорение свободного падения за время падения можно считать постоянным (рис. 20). Сопротивлением воздуха пренебрегаем.

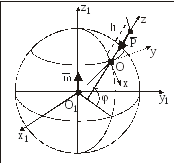
Рис. 20

Начало подвижной системы координат, неизменно связанной с вращающимся земным шаром, возьмем на поверхности Земли в точке О с географической широтой , ось Ох направим на юг по касательной к меридиану, ось Оу – на восток по касательной к параллели, а ось Оz – по вертикали.

Соотношение (2.3) с учетом (2.5) и формулы для примет вид:

,

или

.

Перепишем последнее соотношение, представив векторное произведение в виде определителя и учтя, что - единичные орты подвижной системы координат, составляет угол 90⁰– с осью Оz, а – координаты относительной скорости :

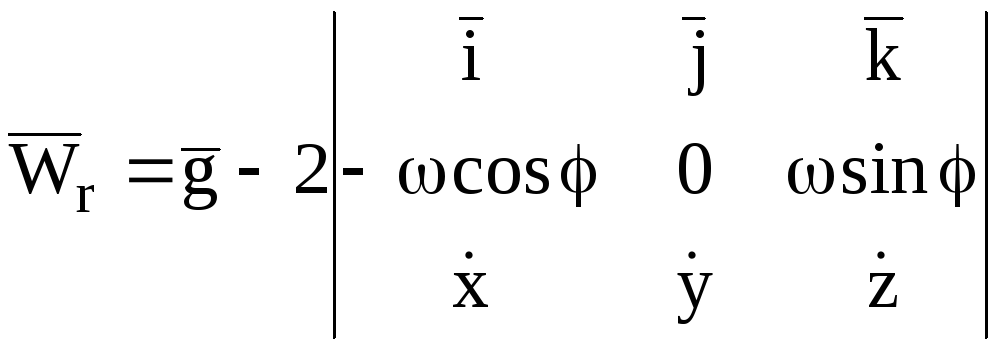. (2.6)

Спроектировав соотношение (2.6) на подвижные оси координат Оxyz, получим дифференциальные уравнения свободно падающей МТ с учетом неинерциальности системы отсчета:

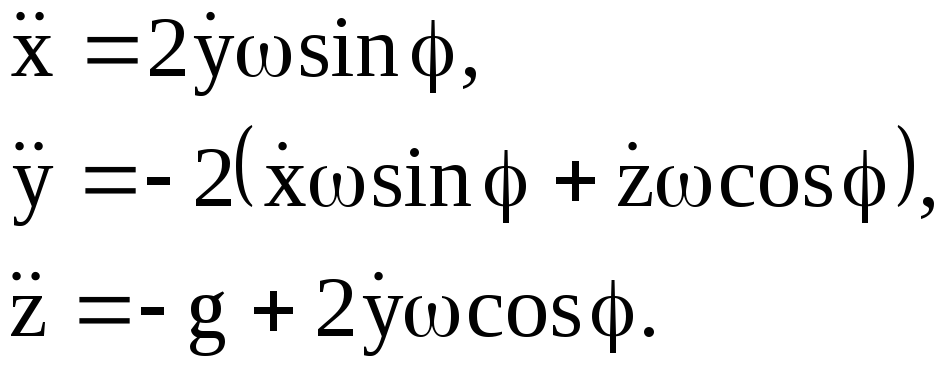(2.7)

Предполагаем, что МТ начинает падать без начальной скорости с высоты h, т.е.

при

(2.8)

Интегрируя уравнение (2.7) с учетом начальных условий (2.8), получим:

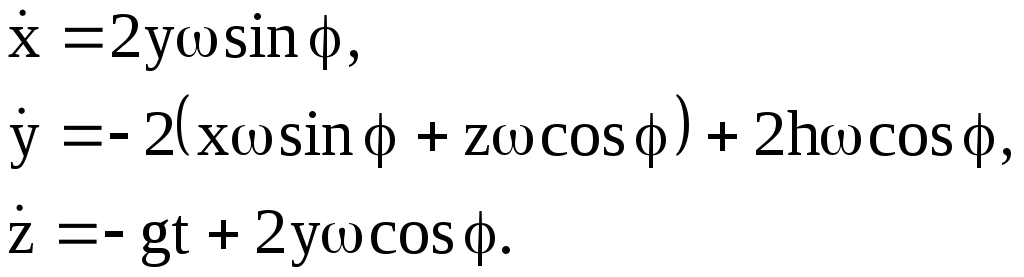(2.9)

Интегрирование системы дифференциальных уравнений (2.9) проведем методом последовательных приближений.

Если пренебречь ускорением Кориолиса, уравнения (2.9) примут вид:

(2.10)

Решением системы дифференциальных уравнений (2.10) при начальных значениях (2.8) будет:

.

Приняв это решение за первое приближение и подставив его в (2.9), получим дифференциальные уравнения второго приближения:

(2.11)

Интегрируя систему дифференциальных уравнений (2.11) с начальными условиями (2.8), получим уравнения движения МТ с учетом вращения Земли, в которых появляется отклонение к востоку (в сторону положительного направления оси у):

(2.12)

Исключив из уравнений (2.12) время t, найдем уравнение траектории МТ:

. (2.13)

Траекторией движения МТ для рассматриваемого второго приближения будет полукубическая парабола (рис. 21).

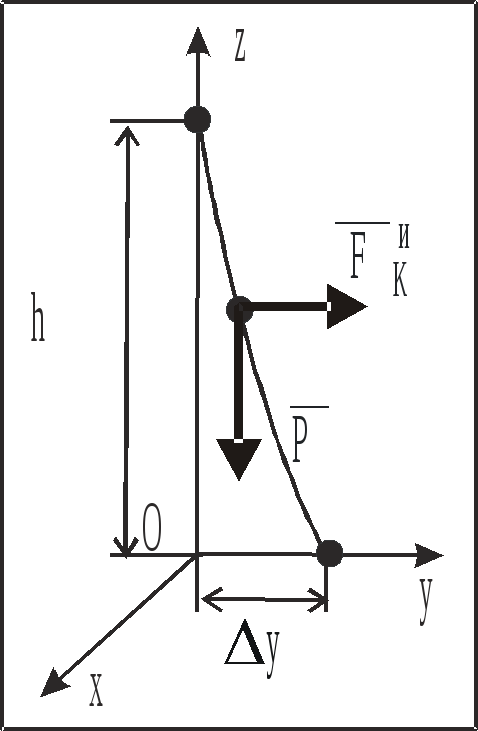
Рис. 21

Отклонение МТ в момент ее падения на поверхность Земли – y найдем, если в уравнении (2.13) положим z=0:

.

Если найти третье приближение, то одновременно с отклонением к востоку появится отклонение к югу, но это отклонение будет очень мало, так как в выражение для x войдет очень малая величина порядка ².

42