Глава 7. Сложное движение мт
7.1. Абсолютное, относительное и переносное движения мт
Определение: движение МТ, рассматриваемое одновременно относительно нескольких систем координат, хотя бы одна из которых неподвижна, называется сложным движением.
Иначе говоря, сложным движением МТ называется такое движение МТ, которое может рассматриваться состоящим из нескольких движений.
При рассмотрении сложного движения МТ оказывается удобным классифицировать движения МТ на абсолютное, относительное и переносное.
Введем неподвижную систему координат О1x1y1z1 и систему координат Oxyz, перемещающуюся относительно системы О1x1y1z1.
МТ, участвующая в сложном движении, перемещается относительно подвижной системы координат Oxyz и вместе с ней относительно неподвижной системы координат О1x1y1z1.
Определение: абсолютным движением МТ называется движение МТ относительно неподвижной системы координат.
Рис. 64
Абсолютное
движение МТ – это ее движение относительно
неподвижной системы координат О1x1y1z1
и
ее уравнением движения будет
(рис. 64).
Все параметры абсолютного движения обозначаются индексом "а".
Определение: относительным движением МТ называется движение МТ относительно подвижной системы координат.
Относительное
движение МТ – это ее движение относительно
подвижной системы координат Oxyz
и ее уравнением движения будет
с координатами x(t),
y(t),
z(t)
(рис. 64).
Все параметры относительного движения обозначаются индексом "r".
Определение: переносным движением МТ называется движение относительно неподвижной системы координат той точки подвижной системы координат, в которой находится в данный момент рассматриваемая точка (иначе говоря, переносное движение МТ – это движение МТ вместе с подвижной системой координат Oxyz относительно неподвижной системы координат О1x1y1z1).
Положение
подвижной системы координат определяется
положением ее начала координат
и направлениями ее осей, которые
определяются единичными ортами
(рис. 64).
Все параметры переносного движения обозначаются индексом "е".
В кинематике сложного движения МТ решаются две задачи:
задача "сложения" – найти абсолютное движение МТ и его кинематические параметры, зная переносное и относительное движения МТ и их кинематические параметры;
задача "разложения" – найти переносное и относительное движения МТ и их кинематические параметры, зная абсолютное движение МТ и его кинематические параметры.
Для решения этих задач необходимо установить зависимости между скоростями и ускорениями абсолютного, относительного и переносного движений МТ.
7.2. Теорема о сложении скоростей мт
В любой момент времени (рис. 64) можно записать, что
и,
учитывая соотношение
получим:
.
(7.1)
В этом выражении:
–определяет
положение МТ в ее абсолютном движении,
x, y, z – определяют положение МТ в ее относительном движении,
,
– определяют положение подвижной
системы координат по отношению к
неподвижной системе координат, т. е.
переносное движение МТ.
Возьмем
производную по времени от выражения
(7.1), учитывая, что единичные вектора
изменяются с течением времени по
направлению:
.
(7.2)
Так
как
– уравнение абсолютного движения МТ,
то в выражении (7.2):
.
(7.3)
Так
как x=x(t),
y=y(t),
z=z(t)
– уравнения относительного движения
МТ (производные от векторов
,
не входят в это выражение, т. е. подвижная
система координат как бы условно
считается неподвижной), то в выражении
(7.2):
.
(7.4)
Так
как
,
определяют положение подвижной системы
координат, т. е. являются параметрами
переносного движения МТ (производные
от координат x,
y,
z
не входят в это выражение, т. е. МТ как
бы не перемещается относительно подвижной
системы координат), то в выражении (7.2):
.
(7.5)
Используя формулу (1.21), получим:
(7.6)
где
— переносная угловая скорость, т. е.
угловая скорость вращения подвижной
системы координат относительно
неподвижной и тогда соотношение (7.5)
примет вид:
.
(7.7)
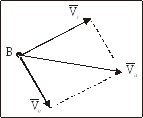
Рис. 65
Подставив выражения (7.3) — (7.5) в выражение (7.2), получим теорему о сложении скоростей в сложном движении МТ:
.
(7.8)
Теорема: Абсолютная скорость сложного движения МТ равна геометрической сумме переносной и относительной скоростей этой МТ (рис. 65).