Лекции

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение:

к² + 2·к +  = 0 имеет корни . (17)

Отсюда видно, что движение будет колебательным, только если ²  . При этом условии корни (17) будут комплексными числами и решением уравнения (16) будет периодическая функция. Представим корни (17) в виде:

, где .

Теперь решением уравнения (16) будет функция: s = е^-βt(С₁cosω₀t + C₂sinω₀t). Заменяя С₁ и С₂ через другие постоянные А₀ и φ₀ такие, что С₁ = А₀cosφ₀ а С₂ = А₀sinφ₀ окончательно получим:

s = А₀е^−βtcos(ωt + φ_○) (18).

Это уравнение свободных затухающих колебаний, график которых представлен на рис. 5. Как видно амплитуда свободных затухающих колебаний убывает по экспоненциальному закону

А = А₀ е^−βt , (19)

(рис.5, пунктирная линия). Круговая частота этого колебания  =, а период Т = 2π/. Как видно ни частота, ни период затухающих колебаний не равны соответствующим параметрам собственных колебаний системы.

Д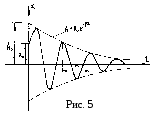ля описания быстроты затухания колебаний используют три взаимосвязанные величины: коэффициент затухания –   , [] = 1/с. Декремент затухания –

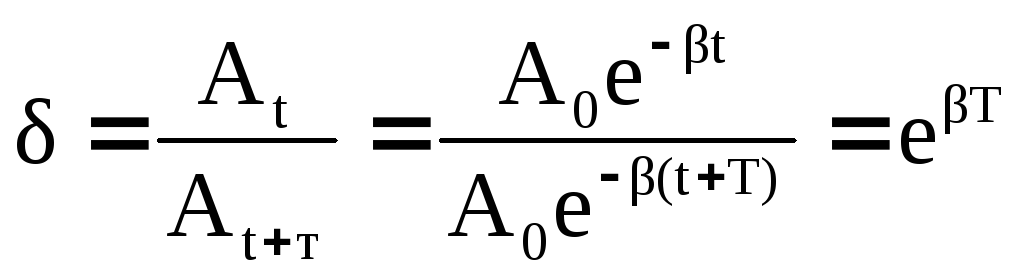(20)

и логарифмический декремент затухания –   ℓn  ℓnе^βТ = βТ. (21)

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Свободные колебания в силу наличия трения всегда будут затухающими. Чтобы колебания были незатухающими необходимо компенсировать потери энергии. Если рассматривать механические колебания, то роль фактора восполняющего эти потери будет играть внешняя переменная сила, которую называют вынуждающей.

Рассмотрим колебания под воздействием вынуждающей силы, изменяющейся по гармоническому закону:

F = F_○соsω_вt. (22)

С учетом квазиупругой силы (1) и силы сопротивления (13) дифференциальное уравнение вынужденных колебаний запишется:

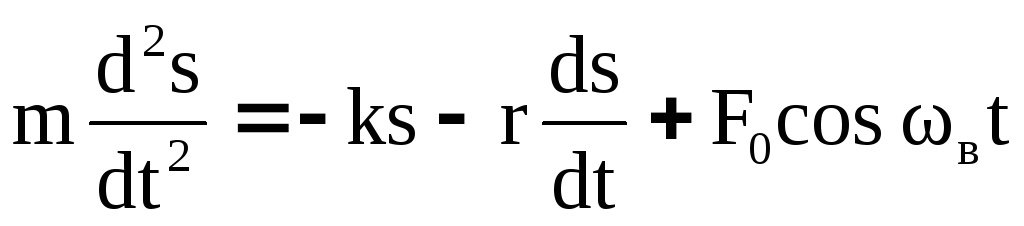(23).

Разделив правую и левую часть на m, и обозначив: 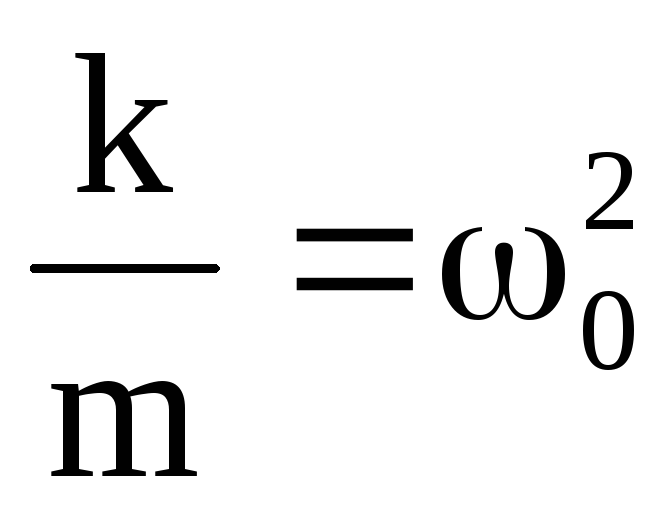, , , после перегруппировки слагаемых, получим неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:

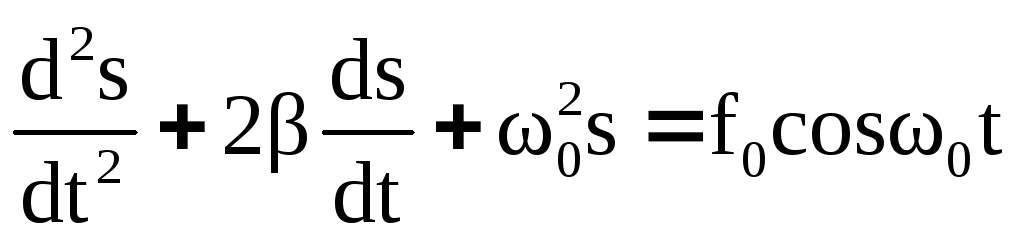(24).

Решением этого уравнения будет функция:

s = Acos(ω_вt+φ₀) (25).

Это уравнение установившихся вынужденных колебаний. Здесь:

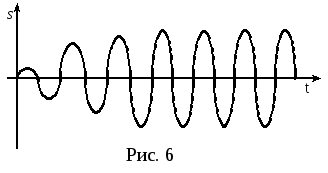
, (26)

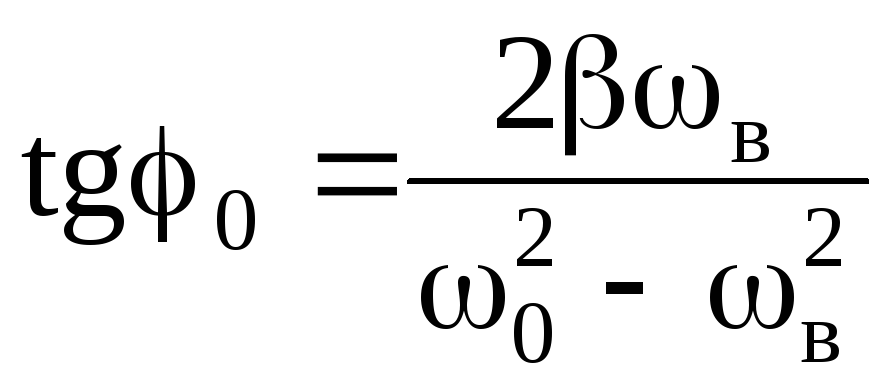. (27)

К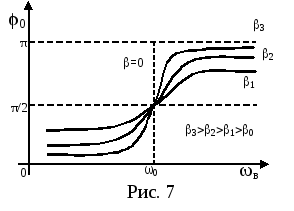ак видно из (25) эти колебания, происходящие под воздействием гармонической вынуждающей силы, тоже будут гармоническими (рис. 6). Их частота равна частоте вынуждающей силы, однако как показывает сопоставление (22) и (25), вынужденные колебания тела отстают по фазе от колебаний вынуждающей силы на φ₀. График зависимости φ ₀ от ω_в при различных значениях β приведен на рис 7.

Из выражения для амплитуды видно, что ее значение зависит от соотношения частоты вынуждающей силы ω_в и собственной частоты колебательной системы ω_о. Очевидно, если подкоренное выражение будет минимально, то амплитуда вынужденных колебаний достигнет своего максимального значения. Исследование на экстремум дает:

-2(ω₀² – ω_в²) ·2ω_в + 8β²ω_в = 0,

ω_в² - ω₀² + 2β² = 0,

что будет иметь место, если

_. (28)

Амплитуда при этом достигает значения

А_рез = 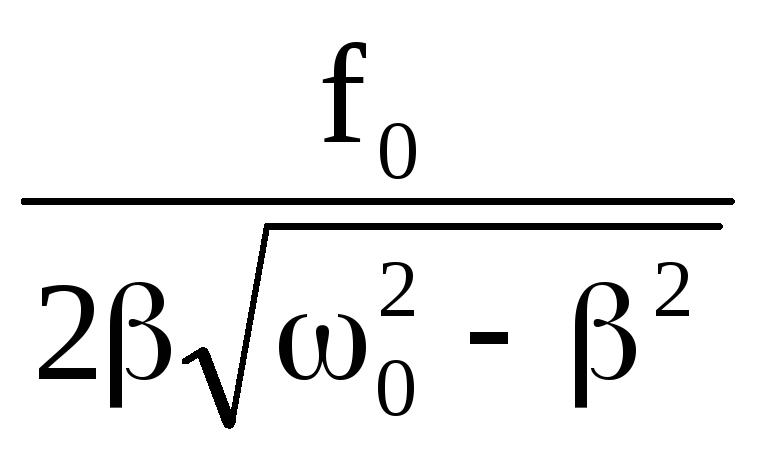. (29)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы получило название резонанса, а соответствующая частота вынуждающей силы – резонансной частотой колебаний.

Приведенные на рис. 8 графики, которые называют резонансными кривыми, отличаются значением коэффициента затухания, действующего в колебательной системе. С уменьшением значения β резонансные кривые становятся все острее, а величина А_рез – все больше. Теоретически при β → 0 частота ω_рез→ ω₀, А → ∞.

Резонанс может иметь как полезные, так и вредные последствия. В одних случаях он может вызвать разрушение, и это приходится учитывать при конструировании мостов, самолетов, высотных домов. В других случаях, наоборот, стремятся создать условия для резонанса, например, при изготовлении музыкальных инструментов, в радиотехнике и т.д.

Автоколебания (качели, часы, электрический колебательный контур) –незатухающие колебания, поддерживаемые внешним источником энергии. Причем поступление энергии регулируется самой колебательной системой.

Параметрические колебания – это колебания, возбуждаемые путем периодического изменения параметров колебательной системы. Пример: шарик на нити, длина которой периодически меняется.

ВОЛНЫ.

Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. При распространении частицы среды последовательно вовлекаются в колебательное движение около своих положений равновесия, но не движутся вместе с волной. Вместе с волной от частицы к частице передается только колебательное движение, а значит, и энергия.

Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные. Они бывают продольные (если колебания ║υ^→) и поперечные (колебания  υ^→).

Волны в общем случае представляют собой пространственное образование. Поверхность, до которой волна дошла в некоторый момент времени, называется фронтом волны.

В зависимости от формы фронта волны бывают волны: плоские, сферические, цилиндрические.

УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

Получим уравнение волны вдоль произвольно выбранного направления ох в однородной среде. Предположим, что в точке О частица совершает колебания по гармоническому закону s₀ = Acosω₀t. Тогда очевидно, что колебание в точке С на оси ОХ будет совершаться с опозданием на некоторое время С по отношению к колебаниям в точке О:

s₀ = Acosω₀(t-τ)

Время запаздывания τ- это время, за которое волновой процесс достигнет точки С. Если скорость волны обозначить через u, а ОС - х, то τ = , и уравнение колебаний в произвольной точке на расстоянии х от источника примет вид:

S_x = Acosω₀(t-τ) = Acosω₀(t-).

Введем понятие длина волны - λ, или расстояние, на которое распространяется волна за время, равное периоду колебаний частиц. Тогда λ = UT = и S = Acosω₀(t-) = Acos2π(v₀t-), т.к. Т = .

В общем случае распространение волн в однородной среде описывается волновым уравнением. Это диф. уравнение второго порядка в частных производных. Найдем его, для чего запишем первые и вторые производные уравнения волны S = Acosω₀(t-) по t и х.

;

;

;

В трехмерном случае:

Скорость распространения продольных механических волн , для поперечных - , где  - плотность недеформированной среды, Е - модуль Юнга, G - модуль сдвига, Е и G - параметры упругости среды.

Свойства волн: прямолинейность распространения в однородной среде, преломление на границе раздела сред, интерференция, дифракция.

Энергия волны. Вектор Умова.

Последовательное вовлечение в колебательное движение частиц среды означает, что волна передает от частицы к частице некоторую механическую энергию. Найдем выражение для энергии, переносимой волной. Рассмотрим для этого некоторый объем среды V. Все частицы этого объема вовлечены волной в колебательное движение. В момент времени t каждая частица массой m занимает свое определенное положение, но ее полная механическая энергия, как мы установили ранее, от этого не зависит и равна Е_пол = . Полагая, что все частицы среды одинаковы, и их в объеме V будет N, получим: .

Р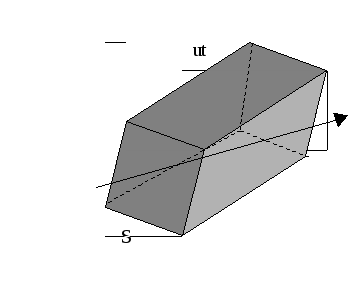азделив правую и левую часть этого равенства на V , получим: объемная плотность энергии, т.е. количество энергии в единице объема волны: , где ρ - плотность вещества среды, в которой распространяется волна. Определим теперь на сечении, перпендикулярном скорости волны , площадку с площадью S.

За время t волна удалится от S на расстояние ut и вовлечет в колебательное движение объем V = S·ut, перенеся при этом через площадку S энергию W = ω∙V = ω∙ S∙ut.

Количество энергии, перенесенное через площадку S за единицу времени, иначе говоря, поток энергии волны Ф = =ω∙ S∙u.

Количество энергии через единицу площади за единицу времени называется интенсивностью энергии волны: .

Т.к. скорость - величина векторная, а ω - скалярная, то слева в этом равенстве должен стоять вектор, т.е. - интенсивность энергии волны в направлении переноса, т.е. называется вектором Умова.

2. Молекулярная физика.

2.1. Основное уравнение молекулярно-кинетической теории газов. Средняя квадратичная скорость молекул газа. Средняя кинетиче­ская энергия поступательного движения молекул газа. Степени свободы. Внутренняя энергия идеального газа. Распределение Максвелла. Барометрическая формула. Распределение Больцмана.

Молекулярная физика изучает круг физических явлений, объяснение которых может быть дано исходя из движения и взаимодействия молекул. Методом молекулярной физики является молекулярно-кинетическая теория, основные положения которой гласят:

1. вещества состоят из мельчайших частиц, атомов или молекул, которые находятся в непрерывном, хаотическом движении;

2. в любом, даже очень малом объеме, к которому еще можно применить выводы молекулярно-кинетической теории, число частиц очень велико;

3. размеры частиц малы по сравнению с расстояниями между ними;

4. соударения частиц между собой и со стенками сосуда являются абсолютно упругими;

5. при отсутствии внешних сил частицы распределяются по всему занятому объему равномерно;

6. по абсолютной величине скорости движения частиц могут изменяться от бесконечно малых до бесконечно больших.

Первая задача, которую мы рассмотрим, состоит в определении величины давления газа на стенки сосуда.

Основное уравнение молекулярно-кинетической теории газа (уравнение Клаузиуса 1857г.)

Воспользуемся моделью идеального газа: размеры его молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда; подавляющую часть времени каждая молекула движется свободно и лишь иногда испытывает упругие столкновения с другими молекулами сосуда. При ударе о стенку молекула воздействует на неё с некоторым импульсом силы (f_mΔt_m). Каждый элемент поверхности стенки непрерывно подвергается "бомбардировке" большим количеством молекул, что и создает определенное силовое воздействие, т.е. давление молекул на стенку. Это силовое воздействие направленно по нормали к стенке.

В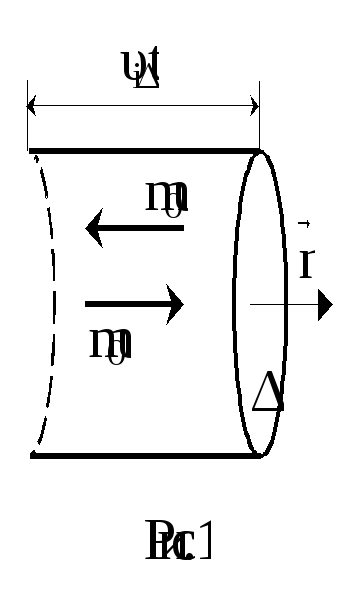ыделим на стенке сосуда произвольную элементарную площадку ΔS (рис.1) и подсчитаем число соударений с ней за время Δt. Очевидно, оно равно числу молекул, которые за это время успеют долететь до элемента ΔS. Понятно, что скорости молекул могут быть самыми различными как по величине, так и по направлению. Кроме того, они беспрерывно меняются при каждом столкновении. Однако, если внешние условия неизменны, то сумма кинетических энергий молекул газа будет величиной постоянной. Так что убывание скорости одной молекулы приводит к возрастанию скорости другой. Принимая во внимание огромное число таких процессов можно считать, что распределение скоростей по значениям неизменно.

Л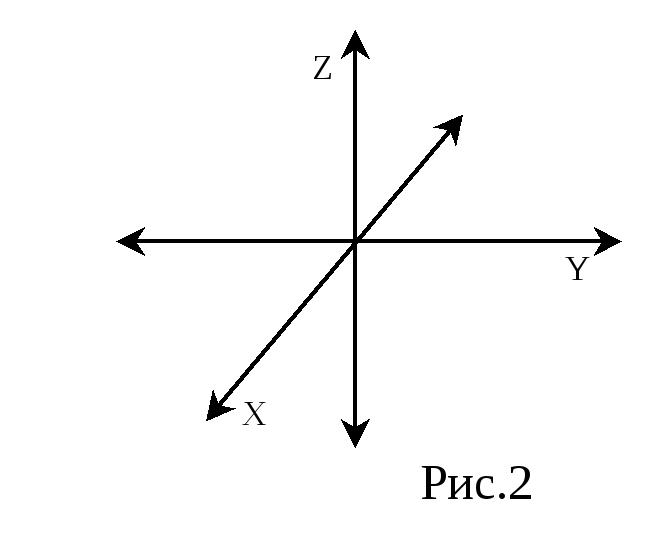юбое движение в пространстве можно рассматривать как движение вдоль трех взаимно перпендикулярных осей: OX, OY, OZ (рис.2), независимо, как эта система координат сориентирована. В силу хаотичности вероятность движения молекул вдоль любого направления одинакова. Тогда условно можно считать, что вдоль любой из осей движется 1/3 всех молекул, причем половина этой трети (т.е. 1/6 от общего числа) – в одну сторону, а вторая половина – в противоположную.

Применим эти рассуждения к прямому цилиндру, построенному на элементе ΔS как основании (рис.1). Рассматривая движение в направлении нормали к ΔS как движение вдоль одной из осей координат (X, Y или Z), получим, что число частиц ΔN_i, имеющих скорость _i и достигших элемента стены ΔS за время Δt:

, (1)

где n_i - число молекул i-ого сорта в единице объема, т.е. таких, которые имеют скорость _i; ∆Ѕ∙υ_i∙∆t - объем цилиндра, содержащего молекулы i-ого сорта, способные долететь до элемента ∆Ѕ за время ∆t. При соударении каждая такая молекула массой m изменяет свой импульс на величину

|∆( mυ_i)| = |- mυ_i- mυ_i| = 2 mυ_i (2).

Тогда, в соответствии с третьим законом Ньютона, стенка получает при единичном соударении импульс силы f_i∙∆t = 2mυ_i , а суммарный импульс, переданный молекулами i-ого сорта элементу ∆Ѕ за время ∆t:

f_i∙∆t = ∆N_i ∙2mυ_i =∙2mυ_i = (3).

Умножим и разделим правую часть равенства на 2:

f_i∙∆t = n_i ∙∙∆Ѕ∙∆t = , (4)

где – кинетическая энергия поступательного движения одной частицы, движущейся со скоростью υ_i.

Полный импульс силы, переданный площадке ∆Ѕ за время ∆t всеми молекулами, будет представлять собой сумму выражений вида (4), записанных для частиц, двигающихся со скоростями υ₁, υ₂, … υ_i … υ_к. к – число сортов молекул:

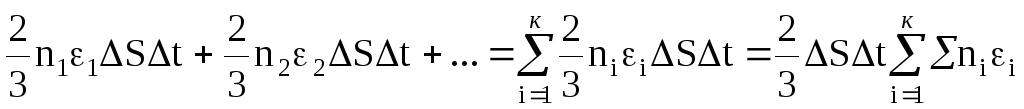
f∆t = (5).

Разделив правую и левую часть (5) на ∆Ѕ∆t, получим:

(6).

- представляет собой суммарную кинетическую энергию молекул в единице объема, т.е. объемную плотность энергии поступательного движения. Обозначим =w. Теперь (6) примет вид:

p = w (7).

Это и есть основное уравнение МКТ, которое гласит: давление идеального газа равно 2/3 кинетической энергии поступательного движения частиц в единице объема.

Рассмотрим другие формы представления основного уравнения МКТ. Введем понятие о средней кинетической энергии молекулы идеального газа как . Тогда w и (7) примет вид:

p = . (8)

Получим ещё один вид основного уравнения МКТ. Для этого выразим среднюю кинетическую энергию молекулы через её скорость:

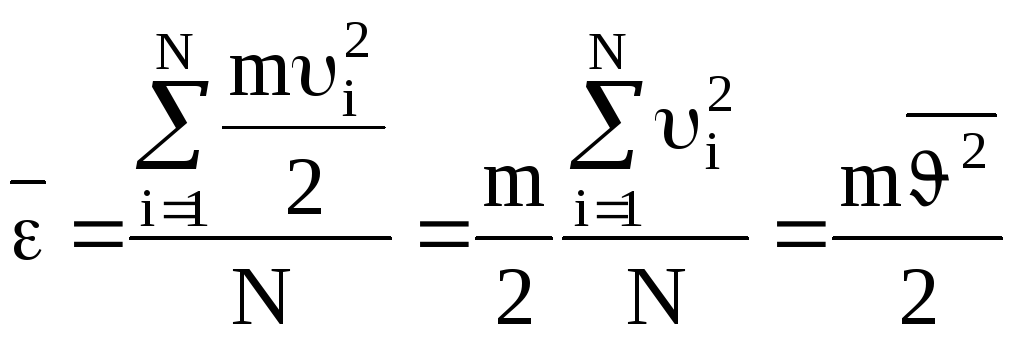. (9)

Здесь, – называется средней квадратичная скоростью частиц (следует иметь ввиду, что ). Теперь с учетом (9):

. (10)

Найдем взаимосвязь с макропараметрами идеального газа. Умножим (8) на молярный объем V_μ :

pV_μ = . (11)

Здесь nV_μ = N_А - число Авогадро. Сопоставляя (11) с уравнением состояния ( уравнение Менделеева-Клапейрона ) для моля идеального газа – pV_μ = RT, имеем RT = , что дает:

. (12)

Здесь, – постоянная Больцмана, k = 1,38∙10^-23 Дж/К.

Формула (12) позволяет сделать очень важный вывод: абсолютная температура идеального газа прямо пропорциональна средней энергии поступательного движения частиц.

как оказывается, этот вывод справедлив не только для газов, но и для любых других агрегатных состояний вещества.

Подставив в (8) из (12), получим:

p = . (13)

Анализ выражения (13) позволяет сделать вывод: т.к. n = , то для любого газа при одних и тех же значениях p и Т концентрация молекул одинакова. Например, при нормальных условиях n = 2,69∙10²⁵ м^-3 - число Лошмидта.

Для смеси газов (13) можно представить в виде:

p = nkT = kT= n₁kT + n₂kT + n₃kT + … n_ikT + … .

Выражение n_ikT = p_i определяет давление, которое создавал бы газ i-ого сорта, если бы в сосуде он был один. Это так называемое парциальное давление газ i-ого сорта. T.o. давление смеси газов равно сумме парциальных давлений соответствующих компонентов:

Р = Р₁ + Р₂ + Р₃… = Р_i – закон Дальтона. (14)

Получим выражение для через макропараметры идеального газа: Из (9) и (12) имеем: . Тогда

; . (15)

Внутренняя энергия идеального газа. Распределение энергии по степеням свободы.

В общем случае внутренняя энергия тела представляет собой сумму всех видов энергии, которыми обладают частицы тела. В молекулярной физике под внутренней энергией идеального газа понимают сумму кинетических энергий всех молекул (молекулярное взаимодействие отсутствует).

Полученное нами выражение для средней кинетической энергии молекулы учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Соответственно, это приводит к изменению трех координат – X,Y,Z, которые определяют его положение в пространстве. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота - α, β, γ. Бильярдный шар на столе имеет две степени свободы поступательного движения и три степени свободы вращательного движения. Соответственно, положение шара на столе можно задать пятью

к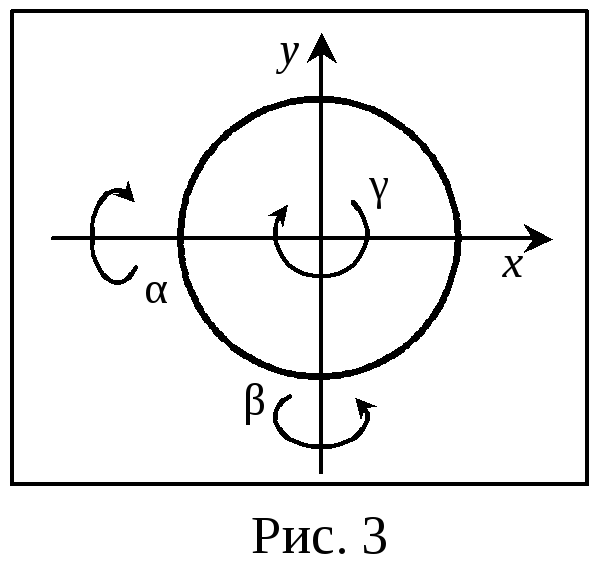оординатами - x, y и α, β, γ. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение системы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. Т.к. выражение (12) определяет энергию молекулы, которая приходится на три степени свободы поступательного движения, тогда на одну степень приходится:

. (16)

Тогда кинетическая энергия каждой отдельной молекулы будет определятся формулой:

. (17)

где j – число степеней свободы молекулы.

Таким образом, проблема внутренней энергии газа сводится к определению числа степеней свободы, которое следует приписать его молекулам. Так как для идеального газа молекулы следует считать материальными точками, то одноатомные газы имеют только три степени свободы поступательного движения (рис.4а). Кинетическая энергия вращательного движения таких молекул бесконечно мала. В приближении шарообразной молекулы, имеем для момента инерции относительно оси вращения проходящей через центр масс – I = 2mr²/5. Но т.к. r → 0, то I ≈ 0.