Тема 2_3: |
Математические основы |
|
криптографии. |
1.Арифметика целых чисел.
2.Модульная арифметика
3.Функция Эйлера
Пантюшин Валерий Алексеевич
кандидат технических наук
Вопрос 1. Арифметика целых чисел.
Основу криптографических преобразований составляют отдельные операции арифметики целых чисел. Высшая арифметика, или теория чисел, изучает свойства натуральных чисел.
К множеству натуральных чисел относят числа N = (…-4,-3,-2,-1,1,2,3,4, …).
Множество целых чисел, содержит все числа (без дробей) от минус бесконечности до плюс бесконечности Z = (…-4,-3,-2,-1,0,1,2,3,4,…).
К рациональным относятся все целые и дробные числа.
Простыми называются числа, которые не имеют собственных множителей – 2,3,5,7,11,13,17,19,23,29,31,37….
Собственным множителем числа А называется множитель отличный от 1 и число А.
То есть, всякое число, кроме единицы, которое делится только на единицу и само на себя, называется простым.
Примечание. Число 1 (единица) не причисляется ни к простым, ни к составным числам.
Составным называется число, которое делится не только на единицу и само на себя, но ещё и на другие числа.
Совершенным числом называется такое число, которое является суммой всех своих положительных собственных множителей. Например 6=1+2+3; 24=1+2+4+7+12.
Вопрос 1. Арифметика целых чисел.
Чтобы узнать, будет ли число простым или составным, его последовательно делят на простые числа, начиная с числа 2.
В таблице представлены простые числа в пределах трех первых сотен.
|
|
Простые числа |
|
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
179 |
181 |
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
269 |
271 |
227 |
281 |
283 |
293 |
307 |
311 |
313 |
317 |
331 |
337 |
347 |
349 |
Вопрос 1. Арифметика целых чисел.
В криптографии нас интересует три бинарных операции в приложении к множеству целых чисел. Бинарные операции имеют два входа и один выход. Для целых чисел определены три общих бинарных операции — сложение, вычитание и умножение. Каждая из этих операций имеет два входа ( a и b ) и выход ( c ).
Деление не относится к этой категории операций. Если мы a делим на n, мы можем получить q и r. Отношения между этими четырьмя целыми числами можно показать как В этом равенстве a называется делимое ; q — частное ; n — делитель и r — остаток. Это уравнением деления не является операцией деления, поскольку результат деления a на n — это два целых числа - q и r.
Вопрос 1. Арифметика целых чисел.
Пример:
Большинство компьютерных языков может найти частное и остаток, используя заданные языком операторы. Например, на языке C оператор "/" может найти частное, а оператор "%" — остаток. (В Excel -?)
Два ограничения:
В криптографии для |
существуют два ограничения: |
1). делитель должен быть положительным целым числом (n>0); 2). остаток является неотрицательным целым числом (r>0).
При отрицательном а, что бы выполнялось ограничение (число r должно быть положительным) поступают следующим образом: уменьшают значение n на 1 и добавляем значение n к r, чтобы r стало положительным.
Здесь уменьшили (–23), получили (–24 ) и добавили 11 к (–2), чтобы получить + 9.
Вопрос 1. Арифметика целых чисел.
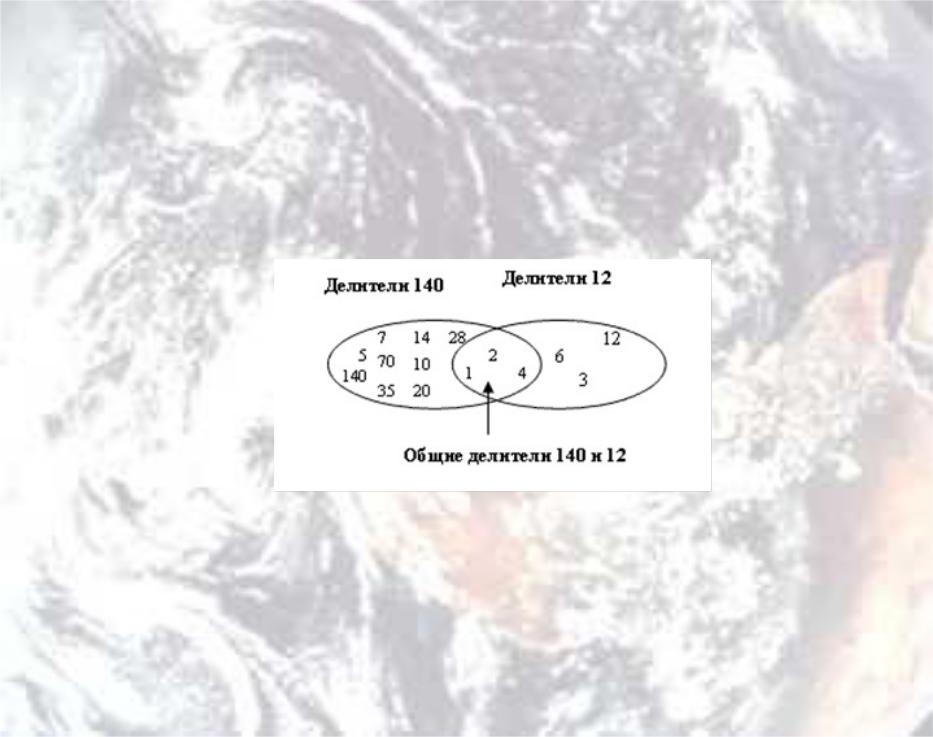
Наиболее часто используемым в методах криптографии является наибольший общий делитель (НОД) двух положительных целых чисел. Два положительных целых числа могут иметь много общих делителей, но только один наибольший общий делитель. Например, общие делители чисел 12 и 140 есть 1, 2 и 4. Однако наибольший общий делитель — 4.
Наибольший общий делитель (НОД) двух положительных целых чисел
— наибольшее целое число, которое делит оба целых числа.
Для определения НОД используется алгоритм Евклида, основанный на двух фактах:
Факт 1: НОД (a, 0) = a;
Факт 2: НОД (a, b) = НОД (b, r), где r — остаток от деления a на b;
Вопрос 1. Арифметика целых чисел.
Первый факт говорит, что если второе целое число — 0, наибольший общий делитель равен первому числу. Второй факт позволяет нам изменять значение a на b, пока b не станет 0. Например, вычисляя НОД (36, 10), мы можем использовать второй факт следующим образом:
НОД(36,10) = НОД(10,6) = НОД(6,4) = НОД(4,2) = НОД(2,0)
или НОД (36, 10) = 2, НОД (10, 6) = 2, и так далее. То есть, вместо вычисления НОД (36,10), мы можем найти НОД (2,0).На схеме показано, использование вышеупомянутых фактов для вычисления НОД (a, b).
Вопрос 1. Арифметика целых чисел.
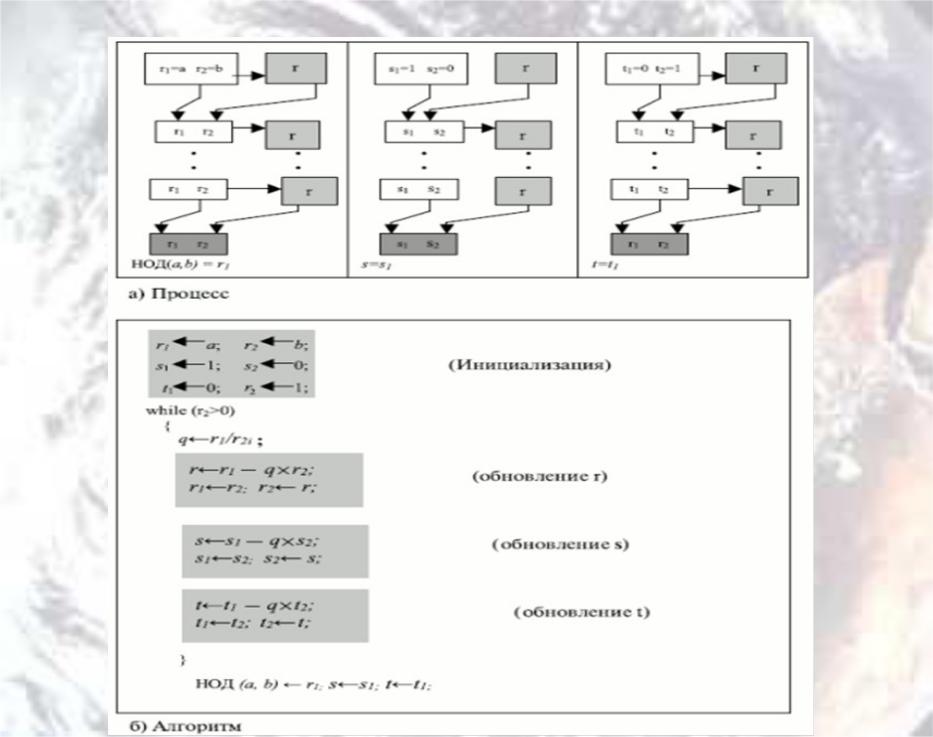
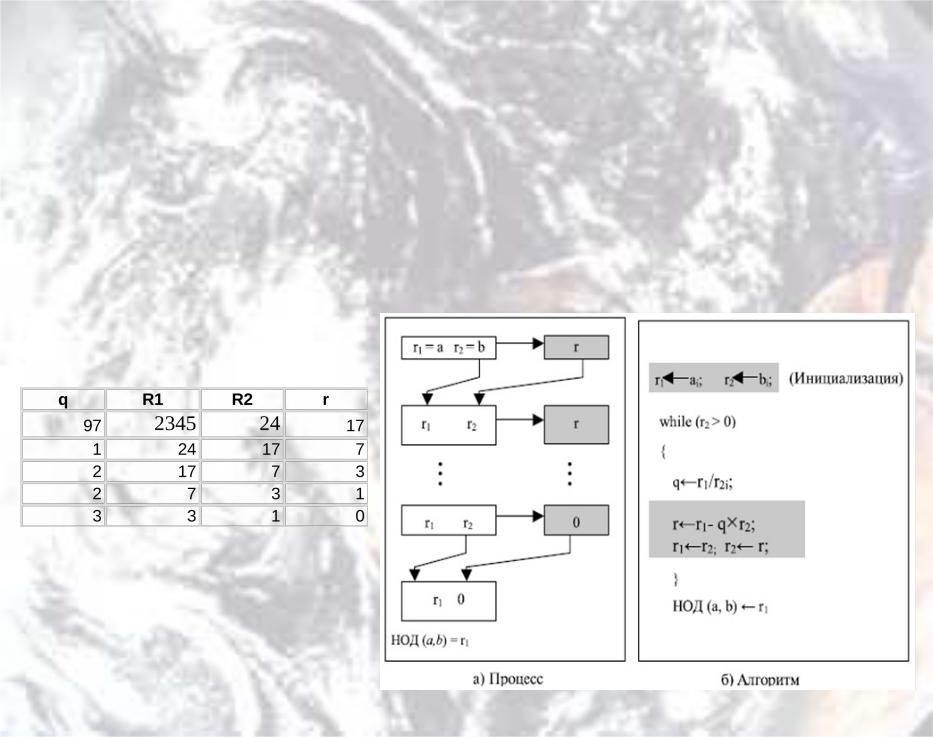
Для определения НОД используются две переменные, r1 и r2, чтобы запоминать изменяющиеся значения в течение всего процесса. Они имеют начальное значение a и b. На каждом шаге вычисляется остаток от деления r1 на r2 и сохраняется результат в виде переменной r. Потом заменяем r1 на r2 и r2 на r и продолжаем шаги, пока r не станет равным 0. В этот момент процесс останавливается и НОД (a, b) равен r1.
Пример алгоритма поиска НОД (2740,1760) показан ниже.
q r1 r2 r
1 |
2740 |
1760 |
980 |
1 |
1760 |
980780 |
|
1980780200
3780200180
1 20018020
9180 20 0
q-целое число от деления r1 на r2; r- остаток от деления r1 на r2;
НОД (2740,1760) = 20 (при условии что r =0) Таким образом мы решили уравнение вида a = b*q + r
Вопрос 1. Арифметика целых чисел.
Расширенный алгоритм Евклида позволяет по известным двум целым числам a и b найти другие два целых числа, s и t, такие, которые удовлетворяют решению следующего уравнения:
s * a + t * b = НОД (a, b)
Расширенный алгоритм Евклида вычисляет НОД (a, b) и в то же самое время позволяет вычислить значения двух других чисел s и t.
Здесь расширенный алгоритм Евклида использует те же самые шаги, что и простой алгоритм Евклида. Однако в каждом шаге мы применяем три группы вычислений вместо одной. Алгоритм использует три набора переменных: r, s и t. Расширенный алгоритм Евклида представлен на следующей схеме.
