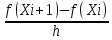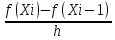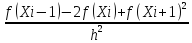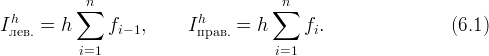Лабораторные работы по численным методам / otchett
.docxМинистерство образования и науки Российской Федерации
Пермский национальный исследовательский политехнический университет
Численные методы.
Вариант 7.
Наименование дисциплины: Вычислительная математика
Преподаватель: Бояршинова И.Н.
Факультет: Информационные системы и технологии
Курс: 2
Группа: ИСТз-13у
Студент: Власова Е.А.
Пермь 2015 г.
Содержание
Лабораторная работа №1. Нелинейные уравнения………………..…………3
Лабораторная работа №2. Численное дифференцирование…………………6
Лабораторная работа №3. Численное интегрирование……………………...7
Лабораторная работа №4. Задачи Коши…………………….………………..9
Приложение А. Нелинейные уравнения. Решение методом Ньютона……..12
Приложение Б. Численное дифференцирование…………………………..…13
Приложение В. Численное интегрирование………………………………….14
Приложение Г. Задачи Коши. Решение методом Эйлера………………..…17
Приложение Д. Задачи Коши.
Решение методом Рунге-Кутты 2го порядка…………………………………18
Приложение Е. Задачи Коши.
Решение методом Рунге-Кутты 4го порядка.……………………………..….19
Лабораторная работа №1
Нелинейные уравнения
Задание:
Для заданного алгебраического уравнения: е0.1хcosx = x
- выбрать отрезок, на котором имеется хотя бы один корень;
- проверить условия применимости (сходимости) методов Ньютона, половинного деления и простых итераций;
- разработать вычислительную программу, реализующую метод, для которого выполнены условия применимости (сходимости);
- вычислить корень уравнения с погрешностью не более 10-6;
- оценить быстродействие вычислительной программы.
Описание методов для решения нелинейных уравнений:
А) Метод Ньютона
Классический
метод Ньютона или касательных заключается
в том, что если 
—
некоторое приближение к корню 
уравнения 
,
то следующее приближение определяется
как корень касательной к функции 
,
проведенной в точке 
.
Уравнение касательной к функции 
в
точке 
имеет
вид:
В уравнении касательной положим 
и 
.
Тогда алгоритм последовательных
вычислений в методе Ньютона состоит в
следующем:
Сходимость метода касательных
квадратичная, порядок сходимости равен
2. Таким образом, сходимость метода
касательных Ньютона очень быстрая.
К
недостаткам метода Ньютона следует
отнести его локальность, поскольку он
гарантированно сходится при произвольном
стартовом приближении только, если
везде выполнено условие 
,
в противной ситуации сходимость есть
лишь в некоторой окрестности корня.
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Б) Метод деления пополам
Простейшим
методом нахождения корней уравнения 
является
метод деления пополам или дихотомия.
Алгоритм
состоит в следующем: Предположим, мы
нашли две точки 
и 
,
такие что 
и 
имеют разные знаки,
тогда между этими точками находится
хотя бы один корень функции 
.
Поделим отрезок 
пополам
и введем среднюю точку 
.
Тогда либо 
,
либо 
.
Оставим ту половину отрезка, для которой
значения на концах имеют разные знаки.
Теперь этот отрезок снова делим пополам
и оставляем ту его часть, на границах
которой функция имеет разные знаки, и
так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область,
где находится корень функции, а,
следовательно, с определенной степенью
точности определим его.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
В) Метод простых итераций
Метод
Ньютона представляет собой частный
случай метода простых итераций.
Здесь 
нетрудно
убедиться, что при 
существует
окрестность корня, в которой 
.
то если 
корень
кратности 
,
то в его окрестности 
и,
следовательно,
.
Если 
—
простой корень, то сходимость метода
касательных квадратичная (то есть
порядок сходимости равен 2). Поскольку 
,
то
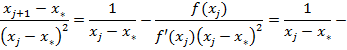
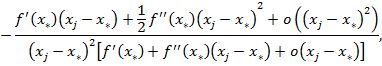
Откуда
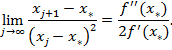
Таким образом, сходимость метода Ньютона очень быстрая.
Так же существуют и другие методы, такие как:
Г) Метод секущих
Чтобы
избежать вычисления производной, метод
Ньютона можно упростить, заменив
производную на приближенное значение,
вычисленное по двум предыдущим точкам:
/
Итерационный
процесс имеет вид:
где 
.
Это
двухшаговый итерационный процесс,
поскольку использует для нахождения
последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже,
чем у метода касательных и равен в случае
однократного корня 
.
Эта замечательная величина называется
золотым сечением:
Д) Метод парабол
Трехшаговый
метод, в котором приближение 
определяется
по трем предыдущим точкам 
, 
и 
.
Для этого заменим, аналогично методу
секущих, функцию 
интерполяционной
параболой проходящей через точки 
, 
и
.
В форме Ньютона она имеет вид:
Точка 
определяется
как тот из корней этого полинома, который
ближе по модулю к точке 
.
Порядок сходимости метода парабол выше,
чем у метода секущих, но ниже, чем у
метода Ньютона.
Важным
отличием от ранее рассмотренных методов,
является то обстоятельство, что даже
если 
вещественна
при вещественных 
и
стартовые приближения выбраны
вещественными, метод парабол может
привести к комплексному корню исходной
задачи.
Этот метод очень удобен для поиска корней многочленов высокой степени.
Результаты:
Решено уравнение: е0.1хcosx = x, на отрезке [1;3]
Корнем уравнения является 0,773207 при х = 3
Лабораторная работа №2
Численное дифференцирование
Задание:
Вычислить приближенно значения 1ой и 2ой производных заданной функций f(x) = sin2 x/(1+sinx)2 в указанной точке 3,0 с помощью разностных аналогов:
Исследовать сходимость численно определяемых значений к точному значению и определить зависимость погрешности численного дифференцирования от шага h.
Описание методов для решения приближенных значений 1ой и 2ой производных заданной функции:
К основным формулам численного дифференцирования относятся три формулы для приближённого вычисления производной (везде далее считаем, что h > 0):
1) правая разностная производная
|
|
2) левая разностная производная
|
|
3) центральная разностная производная
|
|
а также формула второй разностной производной
|
|
Результаты:
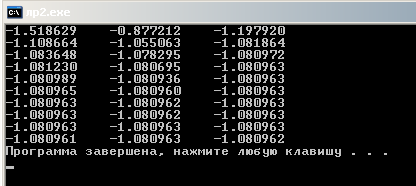
Для заданной функций f(x) = sin2 x/(1+sinx)2 в указанной точке 3,0 приближенное значение будет равно: -1.080961, -1.080962, -1.080963
Лабораторная работа №3
Численное интегрирование
Задание:
Для
определенного интеграла:
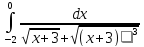
- разработать вычислительную программу, реализующую метод:
а) прямоугольников;
б) трапеций;
в) парабол (Симпсона);
- найти значение заданного интеграла;
- исследовать сходимость численно определяемых значений при уменьшении шагов интегрирования;
- определить зависимость погрешности численного интегрирования от шага интегрирования;
- установить, при каком шаге интегрирования погрешность вычисления интеграла не превышает 10-6;
- оценить быстродействие вычислительной программы.
Описание методов для решения численного интегрирования:
Задача численного интегрирования заключается в замене интеграла
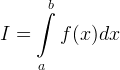конечными
суммами вида
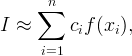
называемыми квадратурными
формулами, где 
—
узлы, а 
—
веса квадратурной формулы. Везде
далее мы будем считать, что отрезок
интегрирования [a,b] разбит
на n отрезков длины 
.
Введём узлы 
, i =
0, 1,…, n. Будем обозначать 
,
где 
—
произвольный индекс.
1) Формулы левых и правых прямоугольников
|
|
Если
подынтегральная функция 
непрерывно
дифференцируема на отрезке [a, b], то
для этих формул справедлива следующая
априорная оценка погрешности:
|
|
2) Формула (центральных) прямоугольников
|
|
где 
, 
.
Если подынтегральная функция 
дважды
непрерывно дифференцируема на
отрезке [a,b], то для формулы справедлива
следующая априорная оценка погрешности:
|
|
3) Формула трапеций
|
|
Если
подынтегральная функция 
дважды
непрерывно дифференцируема на отрезке [a,b],
то для формулы справедлива следующая
априорная оценка погрешности:
|
|
4) Формула парабол (Симпсона)
|
|
Если
подынтегральная функция 
имеет
на отрезке [a,b] непрерывную четвёртую
производную, то для формулы имеет место
следующая априорная оценка погрешности:
|
|
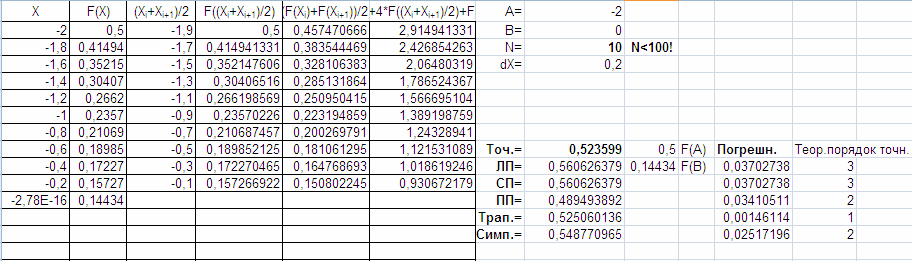
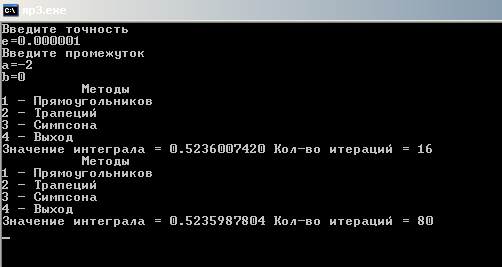
Результаты:
Решение
определенного интеграла:
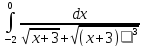будет
равно
0,523599
Лабораторная работа №4
Задачи Коши
Задание:
Для
задачи Коши на заданном интервале: y'
- y/x = x
sin(x),
y|x=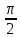
= 1, [
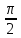,π]
- разработать вычислительную программу, реализующую метод :
а) Эйлера;
б) Рунге – Кутты 2го порядка;
в) Рунге – Кутты 3го порядка;
г) Рунге – Кутты 4го порядка;
д) Адамса;
- найти численное решение дифференциального уравнения;
- исследовать сходимость последовательности численных решений при уменьшающихся шагах интегрирования;
- определить шаг интегрирования, обеспечивающий погрешность численного решения не более 10-6;
- оценить быстродействие вычислительной программы.
Описание методов для решения задачи Коши:
А) Метод Эйлера и модифицированный метод Эйлера
Метод Эйлера является одним из самых простых методов решения дифференциальных уравнений первого порядка: у' = f(х,у). Он в основном используется как учебный, в практических расчетах он дает значительную погрешность. Вычислительный алгоритм представляется следующим образом: Yi+1 = y(xi+h) = yi+D yi = yi+hf(xi,yi
где h –
шаг по х (в общем случае может быть
непостоянным). Запускается метод из
начальных условий: у(х0) = у0.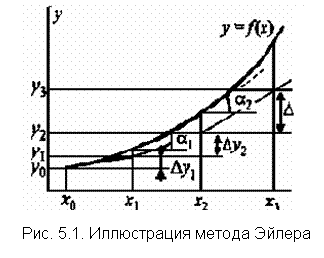
На рис. 5.1 приведена графическая интерпретация метода Эйлера. Величины a1 и a2 определяются из условий: tga1 = f(x0,y0) и tga2 = f(x1,y1);Dу1 = Dx f(x0,y0); Dу2 = Dx f(x1,y1); расчетные значения функции – по соответствующим соотношения
Б)Метод Рунге–Кутта
Существует
целая группа методов Рунге–Кутта, среди
которых наибольшее распространение
получил метод четвертого порядка.
Следовательно, он более точен, чем метод
Эйлера, который является методом первого
порядка . Для расчета одного значения
функции необходимо четыре раза вычислять
правую часть дифференциального уравнения,
а не два, как в модифицированном методе
Эйлера второго порядка. Вычислительный
алгоритм записывается следующим образом:
,
где k1 = h*f (xi,yi); k2 = h*f (xi + h/2, yi + k1/2); k3 =h f (xi + h/2, yi + k2/2); k4 = h f (xi + h, yi + k3).
Здесь также для контроля точности можно применять прием двойного просчета.
Результаты:
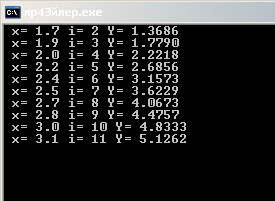
Решение
задачи Коши
y' - y/x = x
sin(x),
y|x=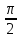
= 1, [
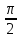,π]
равно:
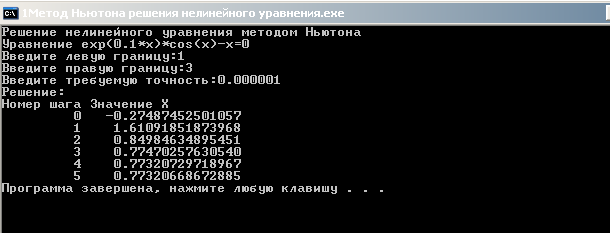
Приложение А. Нелинейные уравнения. Решение методом Ньютона.
program MN1;
uses crt;
function f(x:real):real;
begin
f:=exp(0.1*x)*cos(x)-x;
end;
function f1(x:real):real;
begin
f1:=(-exp(0.1*x)*sin(x))+(0.1*exp(0.1*x)*cos(x))-1;
end;
var a,b,x,e,en:real;
i:integer;
begin
clrscr;
writeln ('Решение нелинейного уравнения методом Ньютона');
writeln ('Уравнение exp(0.1*x)*cos(x)-x=0');
write ('Введите левую границу:'); read(a);
write ('Введите правую границу:'); read(b);
write ('Введите требуемую точность:'); read(e);
writeln ('Решение:');
writeln ('Номер шага Значение X');
en:=abs(a-b);
x:=b;
i:=0;
while (abs(en)>e) do begin
x:=x-f(x)/f1(x);
writeln (i:10,x:20:14);
en:=abs(x-b);
b:=x;
i:=i+1;
end;
end.
writeln ('Решение нелинейного уравнения методом Ньютона');
writeln ('Уравнение exp(0.1*x)*cos(x)-x=0');
write ('Введите левую границу:'); read(a);
write ('Введите правую границу:'); read(b);
write ('Введите требуемую точность:'); read(e);
writeln ('Решение:');
writeln ('Номер шага Значение X');
en:=abs(a-b);
x:=b;
i:=0;
while (abs(en)>e) do begin
x:=x-f(x)/f1(x);
writeln (i:10,x:20:14);
en:=abs(x-b);
b:=x;
i:=i+1;
end;
end.
Приложение Б. Численное дифференцирование.
var i:integer;
x,a,h:real;
b:string;
p1,p2,p3,p4:array [1..10] of real;
s:real;
Function y(x:real):real;
begin
y:=sqrt(sin(x))/(sqrt(1+sin(x)));
end;
begin
x:=3;
h:=0.1;
For i:=1 to 10 do
begin
p1[i]:=(y(x+h)-y(x))/h;
p2[i]:=(y(x)-y(x-h))/h;
p3[i]:=(y(x+h)-y(x-h))/(2*h);
h:=h*0.1;
writeln(p1[i]:4:6,' ',p2[i]:4:6,' ',p3[i]:4:6)
end;
end.
Приложение В. Численное интегрирование.
Program integral;
uses crt;
var x,e,a,b,f:real;
q:char;
n:integer;
pro:real;
procedure mtdprm (a,b,e:real);
label start;
var h,x,s0,s1: real;
i: integer;
function f(x: real): real;
begin
result:=1/(sqrt(x+3)+sqrt((x+3)*(x+3)*(x+3)));
end;
begin
n:=10;
h:=(b-a)/n;
i:=1;
x:=a;
s1:=0;
s0:=0;
start:
while x<b do
begin
s1:=s1+h*f(x);
x:=x+h;
end;
if abs(s1-s0)<e then
begin
writeln('Значение интеграла = ',s1:5:10,' Кол-во итераций = ',i);
end
else
begin
h:=h/2;
s0:=s1;
inc(i);
x:=a;
s1:=0;
goto start;
end;
readln;
end;
procedure mtdtrp (a,b,e:real);
var dx,x,y,integ : real;
n : integer;
function f(x:real):real;
begin
f :=1/(sqrt(x+3)+sqrt((x+3)*(x+3)*(x+3)));
end;
begin
integ:=sin(b*b)-sin(a*a);
n:=10;
y:=0;
while integ - y > e do
begin;
n:=n+1;
dx:=(b-a)/n;
y:=0;
x:=a+dx;
while x<b do
begin
y:=y+f(x);
x:=x+dx;
end;
y:=(y+(f(a)+f(b))/2)*dx;
end;
writeln('Значение интеграла = ',y:5:10,' Кол-во итераций = ',n);
readln;
end;
procedure mtdsmps (a,b,e:real);
label xx2,xy2;
var i1,i2,x1,x2,x0,s,y0,y1,y2,h,x,s0,s1,n: real;
i: integer;
function f(x: real): real;
begin
result:=1/(sqrt(x+3)+sqrt((x+3)*(x+3)*(x+3)));
end;
begin
i1:=0;
n:=10;
h:=(b-a)/n ;
xy2:
i2:=0;
i:=2;
xx2:
x2:=a+i*h;
x1:=x2-h;
x0:=x1-h;
y0:=f(x0);
y1:=f(x1);
y2:=f(x2);
s:=y0+4*y1+y2;
i2:=i2+s;
if i<n then
begin
i:=i+2;
goto xx2;
end
else
begin
i2:=i2*h/3;
if abs(i1-i2)<e then
writeln('Значение интеграла = ',i2:5:10,' Кол-во итераций = ',i)
else
begin
i1:=i2;
n:=n*2;
h:=h/2;
goto xy2;
end;
end;
readln;
end;
label 0,1,2,3;
begin
writeln('Введите точность');
write('e=');read(e);
writeln ('Введите промежуток');
write('a=');read(a);
write('b=');read(b);
f:=1/(sqrt(x+3)+sqrt((x+3)*(x+3)*(x+3)));
0:writeln(' Методы ');
writeln('1 - Прямоугольников');
writeln('2 - Трапеций');
writeln('3 - Симпсона');
writeln('4 - Выход');
q:=readkey;
if q='1' then goto 1
else if q='2' then goto 2
else if q='3' then goto 3
else if q='4' then exit
else begin writeln ('Нет такого');goto 0; end;
1:mtdprm(a,b,e);readkey;
goto 0;
2:mtdtrp(a,b,e);;readkey;
goto 0;
3:mtdsmps(a,b,e);;readkey;
goto 0;
end.
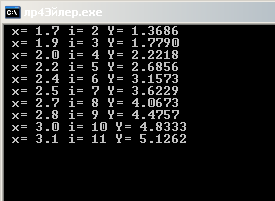
Приложение Г. Задачи Коши. Решение методом Эйлера.
function F(X : real; Y : real):real;
begin
F:= x*sin(x)+(y/x);
end;
var
i, n : Integer;
f1 : real;
h : real;
y1,x1,y, x : real;
begin
x1:=pi; x:=pi/2; n:=10;
y:=1;
h := (x1-x)/n;
y1 := y;
i := 1;
repeat
F1 := F(x, y);
x := x+h;
y := y+F1*h;
y := y1+h*(F1+F(x, y))/2;
y1 := y;
i := i+1;
writeln(' x= ',x:2:1,' i= ',i,' Y= ',y:5:4);
until not (i<=n);
readln;
end.
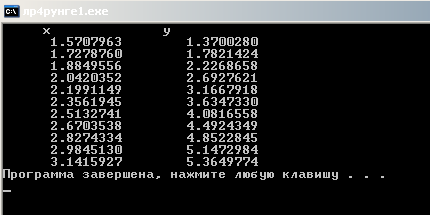
Приложение Д. Задачи Коши. Решение методом Рунге-Кутты 2го порядка.
program rng;
uses crt;
var a,b,x,y,y1,h:real;
i:integer;
function f(x,y:real):real;
begin
f:=x*sin(x)+(y/x);
end;
begin
a:=pi/2;
b:=pi;
h:=(b-a)/10;
y:=1;
x:=a;
clrscr;
writeln(' x',' y');
for i:=1 to 11 do
begin
y1:=y+h*f(x+h/2,y+h/2*f(x,y));
writeln(x:15:7,' ',y1:15:7);
x:=x+h;y:=y1;
readkey;
end;
end.
Приложение Е. Задачи Коши. Решение методом Рунге-Кутты 4го порядка.
program rngk;
Uses crt;
Var
a, b, x0, y0, x1, y1, x2, y2, eps, p, u01, u02, u11, u2, h, g, m, k1, k2, k3, k4: real;
i: integer;
Function f(x,y:real):real;
begin
f:=x*sin(x)+(y/x);
end;
Function u1(x,y,h:real):real;
begin
k1:=f(x,y);
k2:=f(x+h/2,y+h*k1/2);
k3:=f(x+h/2,y+h*k2/2);
k4:=f(x+h,y+h*k3);
u1:=u01+ h*(k1+2*k2+2*k3+k4)/6;
end;
Begin
ClrScr;
write('Введите точность вычесления :E=');
readln(eps);
a:=pi/2;
b:=pi;
h:=(b-a)/10;
y0:=1;
x0:=a;
writeln('X':10,'Y':17,'h':19,'P':20);
u01:=y0;
u02:=y0;
x1:=x0;
x2:=x0;
y1:=y0;
y2:=y0;
While x2<b do
begin
u11:=u1(x1,y1,h);
u01:=u11;
y1:=u11;
x1:=x1+h;
m:=h/2;
u2:=u1(x2,y2,m);
u02:=u2;
y2:=u2;
x2:=x2+m;
u2:=u1(x2,y2,m);
u02:=u2;
g:=y2;
y2:=u2;
x2:=x2+m;
P:=abs(u11-u2);