
схема горнера
.docСхема Горнера
Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида x − c. Метод назван в честь Уильяма Джорджа Горнера (англ.).
Описание алгоритма
Задан многочлен P(x):
![]()
Пусть требуется вычислить значение данного многочлена при фиксированном значении x = x0. Представим многочлен P(x) в следующем виде:
![]()
Определим следующую последовательность:
![]()
![]()
…
![]()
…
![]()
Искомое значение P(x0) = b0. Покажем, что это так.
В полученную форму записи P(x) подставим x = x0 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через bi:
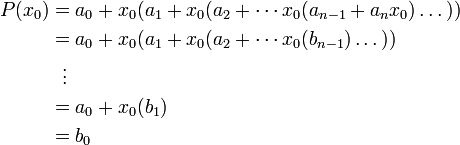
Использование схемы Горнера для деления многочлена на бином
При делении многочлена
![]() на
на
![]() получается многочлен
получается многочлен
![]() с остатком
с остатком
![]() .
.
При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:
![]()
Таким же образом можно определить кратность корня (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням:
![]()
Литература
-
Ананий В. Левитин Глава 6. Метод преобразования: Схема Горнера и возведение в степень // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms — М.: «Вильямс», 2006. — С. 284-291. — ISBN 0-201-74395-7.
-
Волков Е. А. § 2. Вычисление значений многочлена. Схема Горнера // Численные методы — Учеб. пособие для вузов. — 2-е изд., испр. — М.: Наука, 1987. — 248 с.
-
С. Б. Гашков §14. Схема Горнера и перевод из одной позиционной системы в другую // Системы счисления и их применение — М.: МЦНМО, 2004. — С. 37-39. — (Библиотека «Математическое просвещение»). — ISBN 5-94057-146-8.
