
нечітка_логіка-лаб
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ МОРСЬКИЙ УНІВЕРСИТЕТ
«НЕЧІТКА ЛОГІКА»
Методичні вказівки з лабораторних робіт з курсу «Нечітка логіка»
для студентів спеціальності:
Одеса 2015
МЕТИ ОСВОЄННЯ ДИСЦИПЛІНИ «НЕЧІТКА ЛОГІКА»
1.Знайомство з найважливішими поняттями нечіткої логіки і нечіткої математики.
2.Вивчення теоретичних основ, прийомів і методів моделювання.
3.Вироблення практичних навичок дослідження процесів і явищ за допомогою побудування математичних і комп'ютерних моделей з використанням нечіткої логіки і нечіткої математики.
4.Застосування моделювання з використанням нечіткої логіки для вирішення наукових і технічних, фундаментальних і прикладних проблем.
5.Дослідження моделей природничо-наукових, технічних об'єктів і систем.
Урезультаті вивчення навчальної дисципліни «Нечітка логіка» студенти опановують наступними знаннями, вміннями та навичками.
Знання:
про основні поняття і принципи нечіткої математики;
про основні методи і сучасний стан теорії нечіткого моделювання;
класифікації моделей;
моделі фізичних і соціальних явищ з використанням нечіткої логіки;
основні методи дослідження моделей з використанням нечіткої логіки.
Уміння:
будувати математичні та комп'ютерні моделі різних процесів і фізичних явищ на основі нечіткої логіки;
аналізувати отримані результати;
застосовувати основні прийоми моделювання за допомогою нечіткої математики при вирішенні завдань різної природи.
Навички:
розробки моделей фізичних процесів;
розробки моделей навчального процесу;
володіння методами планування експерименту, методами збору, обробки та подання інформації, моделюючими процедурами програмно-методичних комплексів.
ВСТУП
Нечітка логіка використовуються в тих випадках, коли побудова, а потім і реалізація математичної моделі утруднене, або не представляється можливим через складність модельованої системи (процесу), наявності невизначеностей, що супроводжують процеси, що протікають в системі.
Основними поняттями нечіткої логіки є поняття: лінгвістична змінна, нечіткі множини, функції приналежності.
Лінгвістичними називаються змінні, значеннями яких є терми (слова, речення). З терміном "лінгвістична змінна" можна пов'язати будь-яку фізичну змінну, для якої потрібно мати більше значень, ніж, та й немає. Значення лінгвістичної змінної прийнято називати термами.
Належність кожного точного значення до одного з термів визначається за допомогою функцій належності. Існує кілька типів стандартних функцій приналежності: трикутна (trimf), трапецеїдальних (trapmf), гауссова (gaussmf), подвійна гауссова (gauss2mf), узагальнена колоколообразная (gbellmf), сигмоїдальна (dsigmf), твір двох сигмоїдальних функцій (psigmf), Z-функція , S- функція, Piфункція.
В цілому процес обчислення в нечітких системах відбувається в кілька етапів:
1) фазифікація - процес переходу від "чіткого" (виміряного, наприклад
t70) значення до "нечіткому" ( t середня).
2)нечіткий логічний висновок. На даному етапі на основі правил, закладених на етапі проектування в базу правил нечіткої системи, відбувається визначення значення вихідної змінної.
Дані правила описують відносини між лінгвістичними змінними за допомогою нечітких висловлювань, пропозицій сформульованих у вигляді "Якщо
-То" (нечіткі інструкції). При наявності двох вхідних величин "Якщо - То" правила складаються з двох умов і об'єднуються логічною операцією AND або OR. Сукупність нечітких правил (нечітких інструкцій) прийнято називати алгоритмом нечіткого виводу. Наприклад, Якщо t = середня Те P = висока. Як видно, значення вихідної змінної в результаті нечіткого логічного висновку також є нечітким.
3)На останньому етапі, який прийнято називати дефаззіфікацією, здійснюється перехід від нечітких значень до чітких. Дефаззіфікація можлива одним з таких методів: метод центру тяжіння, модифікований метод тяжкості, метод максимуму, метод лівого максимуму, метод правого максимуму.
ЛАБОРАТОРНА РОБОТА №1 ОСНОВИ ЗАСТОСУВАННЯ НЕЧІТКОЇ ЛОГІКИ. СПОСОБИ ЗАВДАННЯ І
КОРЕКЦІЇ ФУНКЦІЙ НАЛЕЖНОСТІ НЕЧІТКИХ МНОЖИН
Мета роботи:
вивчення основних способів завдання функцій приналежності нечітких
множин;
ознайомлення зі способами побудови та корекції функцій приналежності
впакеті програм MATLAB;
набуття практичних навичок роботи в пакеті MATLAB з побудови функцій належності нечітких множин.
1. Застосування нечіткої логіки
При вирішенні погано формалізованих задач можуть бути використані методи еволюційних обчислень і, зокрема, генетичні алгоритми. При цьому порівняно важко перевірити якість результату, отриманого в процесі роботи таких алгоритмів. Оцінити ступінь якості результату рішення погано формалізованої задачі можна з використанням методів нечіткої логіки.
Нечітка логіка (fuzzy logic) - це надмножина класичної булевої логіки. Вона розширює можливості класичної логіки, дозволяючи застосовувати концепцію невизначеності в логічних висновках.
В основі нечіткої логіки лежить теорія нечітких підмножин (нечітких множин). Ця теорія займається розглядом множин, що визначаються небінарнимі відносинами входження. Це означає, що береться до уваги не просто те, входить елемент у безліч або не входить, але і ступінь його входження, яка може змінюватися від 0 до 1.
Нечітка підмножина F може бути представлено, як відображення безлічі S на інтервал I = [0, 1]. Це відображення визначається безліччю впорядкованих пар:si , mF si , i 1, n , де si - i-й елемент множини S; n - потужність множини S;
mF si 0,1 |
- ступінь входження елемента в безліч F. Значення |
mF si , рівне 1, |
||
означає повне входження, |
mF si 0 |
вказує на те, що елемент |
si не належить |
|
безлічі F. |
|
|
|
mF x нечіткій |
Часто |
відображення |
задається |
функцією приналежності |
|
множині F. У силу цього терміни «нечітке підмножина» і «функція приналежності» вживаються як синоніми. Ступінь істинності предиката « sk F »
визначається шляхом знаходження парному елементу sk значення mF sk , що визначає ступінь входження sk в F.
Узагальнюючи геометричну інтерпретацію традиційного підмножини на нечіткий випадок, отримуємо уявлення F точкою в гіперкубі In, I = [0,1] (рис.1). На відміну від традиційних підмножин точки, що зображують нечіткі підмножини, можуть перебувати не тільки на вершинах гиперкуба, але і всередині нього.
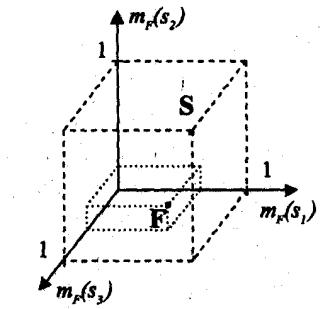
Рис. 1 – Графічний вигляд нечіткої підмножини
Нечітке правило логічного висновку є впорядкованою парою (A, B), де A - нечітка підмножина простору вхідних значень X, B - нечітке підмножина
простору вихідних значень Y. Система нечіткого виводу - це відображення Iразм(X) в Iразм(Y), де разм(Z) - оператор визначення простору Z. Число елементів в Iразм(X) іі
Iразм(Y) нескінченно велике, тому не можливо задати правила нечіткого висновку відповідними парами точок. Однак вони можуть бути описані в термінах теорії нечітких множин. Нечіткі правила виведення утворюють базу правил. Важливо те, що в нечіткій експертній системі на відміну від традиційної працюють всі правила одночасно, але ступінь їх впливу на вихід може бути різною. Принцип обчислення суперпозиції багатьох впливів на остаточний результат лежить в основі нечітких експертних систем.
Процес обробки нечітких правил виводу в експертній системі складається з
4етапів:
1.Обчислення ступеня істинності лівих частин правил (між "якщо" і "то") - визначення ступеня приналежності вхідних значень нечітким підмножини, зазначеним у лівій частині правил виводу.
2.Модифікація нечітких підмножин, зазначених у правій частині правил виводу (після "то"), відповідно до значень істинності, отриманими на першому етапі.
3.Об'єднання (суперпозиція) модифікованих підмножин.
4.Скаляризації результату суперпозиції - перехід від нечітких підмножин до скалярним значенням.
Для визначення ступеня істинності лівій частині кожного правила нечітка експертна система обчислює значення функцій належності нечітких підмножин від відповідних значень вхідних змінних.
Отримане значення істинності використовується для модифікацій нечіткої множини, зазначеного в правій частині правила. Для виконання такої модифікації використовують один з двох методів: "мінімуму" і "твори". Перший метод
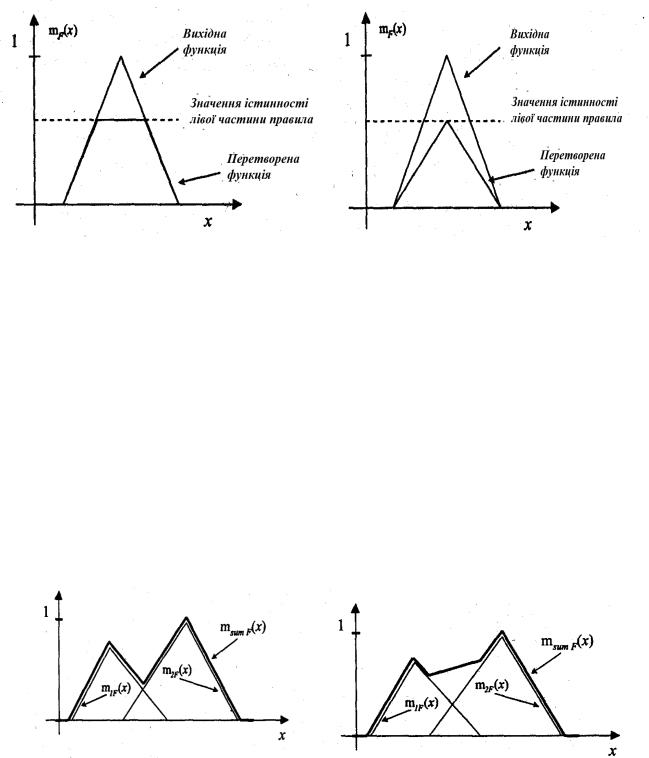
обмежує функцію приналежності для безлічі, зазначеного в правій частині правила, значенням істинної лівій частині (Рис.2).
У другому методі значення істинності лівій частині використовується як коефіцієнт, на який множаться значення функції приналежності (Рис.3).
Рис. 2 - Метод «мінімуму» Рис. 3 - Метод «добутку»
Результат виконання правила - нечітка множина, тобто відбувається асоціювання змінної і функції приналежності, зазначених у правій частині.
Виходи всіх правил обчислюються нечіткої експертної системою окремо, проте в правій частині декількох з них може бути вказана одна і та ж нечітка змінна. Для цього система виробляє суперпозицію нечітких множин, пов'язаних з кожною з таких змінних. Ця операція називається нечітким об'єднанням правил
виводу. |
|
|
Традиційно суперпозиція функцій приналежності нечітких |
множин |
|
m1F x , m2 F x ,..., mnF x визначається як |
msumF x max miF x x, i 1, n . |
Графічне |
представлення подібної суперпозиції представлено на рис.4.
Інший метод суперпозиції полягає в підсумовуванні значень всіх функцій
n |
x x, i 1, n (графічна інтерпретація наведена на |
приналежності msumF x miF |
|
i 1 |
|
рис.5). |
|
Рис. 4 - Метод «Max Combination» Рис. 5 - Метод «Sum Combination»
Кінцевий етап обробки бази правил виводу - перехід від нечітких значень до конкретних скалярним. Процес перетворення нечіткої множини в єдине значення називається "скаляризації" або "дефазифікації" (defuzzification). Найчастіше як

такого значення використовується "центр ваги" функції приналежності нечіткої множини (centroid defuzzification method) (Рис.6). Також припустима скаляризації методом «максимуму» - вибір максимального значення суперпозиції функцій приналежності.
Рис. 6 – Скаляризація методом «центру ваги»
2. Способи завдання функцій приналежності
Нечіткою безліччю A на універсальній множині U називається сукупність пар (μА (u), u) , де μА (u) - ступінь належності елемента u U нечіткій множині
A . Ступінь приналежності - це число з діапазону [0,1]. Чим вище ступінь приналежності, тим більшою мірою елемент універсальної множини відповідає властивостям нечіткої множини.
Функцією приналежності називається функція, що дозволяє для довільного елемента універсальної множини обчислити ступінь його належності нечіткій
множині. |
|
У разі |
безперервної |
безлічі |
U |
|
|
використовують |
позначення |
||||||||||||||||||||||||||||
|
|
|
|
μ |
А (u) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
. Знак |
позначає безперервну сукупність величин, а не операцію |
|||||||||||||||||||||||||||||||||
|
u |
|
|||||||||||||||||||||||||||||||||||
|
|
|
u U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
інтегрування. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U u1,u2,...,uk , |
|
|||||||||||||||||
|
|
|
Якщо універсальне безліч є кінцевим |
тоді нечітка |
|||||||||||||||||||||||||||||||||
множина А записується як: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
k μ |
|
(u |
|
) |
|
|
μ |
(u ) μ |
|
(u |
|
) |
|
μ |
|
(u |
|
) |
|
|||||||||
|
|
|
|
|
|
A |
|
|
|
А |
|
|
i |
|
чи |
A |
|
|
А 1 |
, |
|
А |
|
|
2 |
|
,..., |
|
А |
|
|
k |
|
|
(1) |
||
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
i |
|
|
|
|
|
u |
2 |
|
|
u |
2 |
|
|
|
|
u |
k |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де - це символ дискретної операції.
3. Порядок виконання роботи
1.Ознайомитися з основними способами завдання функцій приналежності нечітких множин.
2.Описати задані нечіткі змінні з використанням 3¬4 функцій приналежності.
3.Побудувати графіки усіх функцій приналежності.
4.Оформити звіт про виконану роботу.
5.Відповісти на контрольні питання.
4. Контрольні питання
1.Які змінні називаються лінгвістичними?
2.Які етапи включає в себе процес проектування нечітких систем?
3.У чому полягає процес фазифікації?
4.У чому полягає процес дефаззіфікації?
5.Які методи дефаззіфікації можуть використовуватися при побудові нечітких систем? У чому ці методи полягають?
6.Як формулюються правила нечіткого висновку для випадку однієї вхідної змінної, для випадку двох вхідних змінних?
ЛАБОРАТОРНА РОБОТА №2
МЕТОДИ ПОБУДОВИ ФУНКЦІЙ ПРИНАЛЕЖНОСТІ В MATLAB З ВИКОРИСТАННЯМ ПАКЕТУ FUZZY LOGIC TOOLBOX
Мета роботи:
вивчення основних видів функцій приналежності нечітких множин;
ознайомлення зі складом і можливостями інструментарію нечіткої логіки Fuzzy Logic Toolbox, що входить в пакет програм MATLAB;
набуття практичних навичок роботи в пакеті Fuzzy Logic Toolbox.
1. Способи формування функцій належності в середовищі MATLAB
Інструментарій нечіткої логіки в складі пакету MATLAB містить 11 вбудованих типів функцій приналежності, формованих на основі кусковолінійних функцій, розподілу Гаусса, сігмоідной кривої, квадратичних і кубічних поліноміальних кривих. До найбільш простим ФП можна віднести трикутну і трапецієподібну.
Опис трикутної функції приналежності в MATLAB:
y trimf(x, [a b c]) , |
(2) |
де вектор x - базове безліч, на якому визначається ФП. Величини і задають основу трикутника, b - його вершину.
В аналітичному вигляді трикутна ФП може бути задана наступним чином:
|
0, x a, |
|
||||
|
x - a |
, a x b, |
|
|||
|
|
|
|
|
|
|
|
b - a |
|
||||
f(x, |
a b c) с - x |
, b x c, |
(3) |
|||
|
|
|
|
|
|
|
|
c - b |
|
||||
|
|
с. |
|
|||
|
0, x |
|
||||
Приклад використання трикутної функції в системі MATLAB: |
|
|||||
x = 0: 0.1: 10; % Завдання базового безлічі |
|
|||||
y = trimf (x, [4 6 8]); % Визначається трикутна ФП |
|
|||||
plot (x, y); % Виводиться графік функції |
|
|||||
xlabel ('trimf (x, P), P = [ 4 6 8]'); % Підписується графік |
|
|||||
під віссю абсцис |
|
|
|
|
|
|
Трапецієвидна ФП: |
|
|
|
|
|
|
y trapmf(x, [a b |
c d]) , |
(4) |
||||
де вектор x - базове безліч, на якому визначається ФП. Величини a і d |
||||||
задають нижню підставу трапеції, b і c - верхнє підставу. |
|
|||||
Аналітичний вид трапецієподібної ФП: |
|
|
||||
|
0, x a, |
|
||||
|
|
x - a |
, a x b, |
|
||
|
b - a |
|
||||
f(x, a, |
b, c, d) 1, b x c, |
(5) |
||||
|
с - x |
, с x d, |
|
|||
|
|
|
|
|
||
|
|
|
||||
|
c - b |
|
||||
|
0, x d. |
|
||||
|
|
|
|
|||
Приклад використання трапецієподібної ФП в системі MATLAB:
x = 0: 0.1: 10; % Завдання базового безлічі
y = trapmf (x, [1 4 7 8]); % визначається трапециевидная ФП plot (x, y); % Виводиться графік функції
xlabel ('trapmf (x, P), P = [1 4 7 8]'); % Підписується графік під віссю абсцис
Одним з основних переваг розглянутих вище функцій є їх простота, реалізація даних функцій у системі MATLAB зображена на рис. 7.
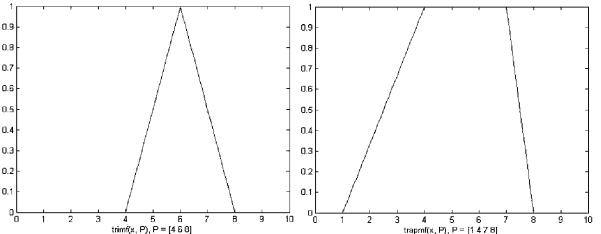
Рис. 7 - Трикутна і трапецієвидна функції приналежності
На основі функції розподілу Гауса можна побудувати ФП двох видів: просту функцію приналежності Гаусса і двосторонню, утворену за допомогою різних функцій розподілу Гаусса (рис.8).
Функція gaussmf задає функцію приналежності у вигляді симетричною гауссовської кривої. Ця функція аналітично задається формулою:
|
- (x - c)2 |
|
|
f(x, ,c) e |
2 |
2 |
(6) |
|
|
||
Параметри функції gaussmf геометрично інтерпретуються наступним чином:
c - координата максимуму функції належності;
- коефіцієнт концентрації функції приналежності.
Функція gaussmf застосовується для завдання гладких симетричних функцій приналежності. Синтаксис функції:
y gaussmf(x, params) |
(7) |
Функція gaussmf має два вхідних аргументи:
x - вектор, для координат якого необхідно розрахувати ступеня належності; params - вектор параметрів функції належності. Порядок завдання
параметрів -[ ,c]
Функція повертає вихідний аргумент у вигляді масиву, що містить ступеня приналежності координат вектора.
Двостороння гауссовська функція приналежності задається виразом
y gauss2mf(x , params) |
(8) |
Ця функція приналежності складається з комбінації двох гауссовських функцій приналежності:
