38

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ОДЕССКИЙ НАЦИОНАЛЬНЫЙ МОРСКОЙ УНИВЕРСИТЕТ

Кафедра «Техническая кибернетика»

«Исследование динамических систем»

курсовой проект по дисциплине

«Моделирование систем»

Выполнил:

студент КСФ 3к. 4гр.

Борщенко Д.А.

Проверили:

Челабчи В.Н.,

Челабчи В.В.

Одесса – 2013

СОДЕРЖАНИЕ:

1 ИДЕНТИФИКАЦИЯ ОБЫКНОВЕННОГО ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1ГО ПОРЯДКА 3

1.1 Постановка задачи 3

1.2 Описание используемых методов 3

1.2.1 Аппроксимация на смежных отрезках 3

1.2.1 Аппроксимация на скользящих интервалах 4

1.3 . Результаты решения задачи аппроксимации 5

1.3.1 Проведение идентификации в среде Excel 5

1.3.2 Проведение идентификации в среде Delphi 11

1.3.3 Проверка и сравнение результатов идентификации 16

1.4 Заключение 18

2 ИССЛЕДОВАНИЕ ДИНАМИКИ СИСТЕМЫ 19

2.1 Постановка задачи 19

2.2 Запись конечно-разностных аналогов дифференциальных уравнений 20

2.3 Решение в среде Excel 21

2.4 Решение в среде Delphi 22

2.5 Заключение 25

ЛИТЕРАТУРА 26

ПРИЛОЖЕНИЕ 1 27

ПРИЛОЖЕНИЕ 2 31

1 Идентификация обыкновенного линейного дифференциального уравнения 1го порядка

1.1 Постановка задачи

Существует физический объект, процесс в котором отражается параметром Y(τ). Величина Y изменяется во времени в зависимости от воздействия X(τ). Свойства объекта постоянны. Предполагается, что процесс в объекте описывается обыкновенным линейным дифференциальным уравнением первого порядка с постоянными коэффициентами:

, (1.1)

где τ- время,

X(τ) - воздействие,

Y(τ) - реакция объекта,

А, K- коэффициенты, отражающие свойства объекта.

1.2 Описание используемых методов

1.2.1 Аппроксимация на смежных отрезках

Всю область изменения величин X(τ) и Y(τ) разбивается на участки, которые следуют друг за другом или перекрывают друг друга (Рис. 1.1).

Рисунок.1.1 - Схема разбиения области.

На каждом i^омучастке зависимость Y() аппроксимируется полиномами невысоких степеней вида:

, (1.2)

где - локальная (в пределахi^гоучастка) координата времени. Откуда:

, (1.3)

Выражение для суммы квадратов невязок по всем рассмотренным зонам имеет вид:

, (1.4)

где m – количество рассмотренных точек всей области определения функции (включая все выделенные интервалы), j– индекс точки.

Необходимым условием минимума функции S является равенство нулю ее частных производных:

(1.5)

Откуда следует

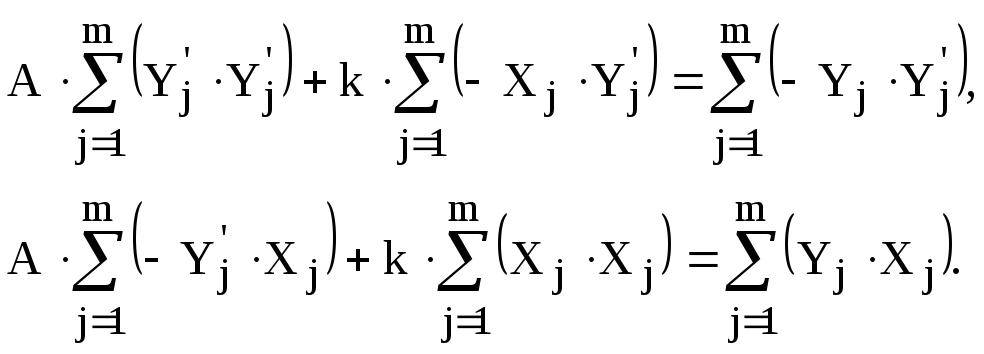(1.6)

Решив систему линейных алгебраических уравнений (1.6), получим значения A, k.

1.2.1 Аппроксимация на скользящих интервалах

Можно использовать подход, позволяющий проводить идентификацию при любом характере воздействия. Кроме того, учитывается, что зависимости X(τ) и Y(τ) могут быть зашумлены.

Выбирается метод наименьших квадратов с аппроксимацией зависимостей X=f(τ) и Y=f(τ) на интервалах времени, при котором:

• проводится аппроксимация зависимостей X=f(τ) и Y=f(τ) на интервалах оси времени гладкими функциями (полиномы невысоких степеней);

• для моментов времени путем дифференцирования аппроксимирующей функций определяются производные Y’ и значения X, Y;

• значения функций и производных подставляются в идентифицируемое уравнение и определяется сумма квадратов невязок левой и правой частей уравнения для всех рассматриваемых моментов времени;

• значения коэффициентов идентифицируемого дифференциального уравнения определяются путем минимизации суммы квадратов невязок левой и правой частей уравнения.

В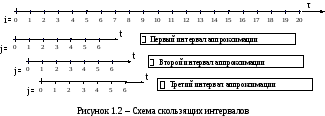торой особенностью метода является организация обработки данных для идентификации.

Экспериментальные данные представляются совокупностью записей, каждая из которых содержит: значение момента времени τ_i, значение воздействия Xе_i, значение реакции объекта Yе_i

Из совокупности записей выделяются выборки (интервалы времени) для каждой из которых вводится новая независимая переменная t.

Зависимости X(t) и Y(t) в пределах каждого интервала (выборки записей) аппроксимируются полиномами невысоких степеней.

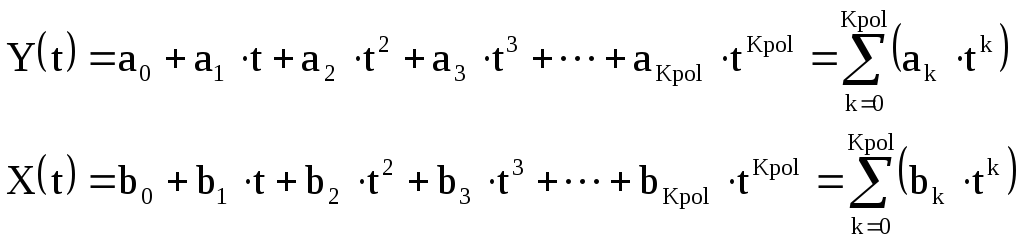(1.7)

где а₀а_Kpolиb₀b_Kpol- коэффициенты аппроксимирующих полиномов,Kpol– порядок аппроксимирующего полинома.

Выбранный способ представления данных для проведения аппроксимации экспериментальных зависимостей Xе(τ) и Yе(τ) отличается тем, что он не требует равномерного расположения моментов времени на оси τ.

Другим достоинством принятого способа является возможность существенного перекрытия интервалов времени при аппроксимации, что заметно повышает достоверность результатов идентификации.

При идентификации уравнения (1) минимизируемый функционал S имеет вид:

. (1.8)

Минимум S достигается при выполнении условий:

, .

Что приводит к системе линейных алгебраических уравнений:

(1.9)