дискр мат / СДНФ

9

СДНФ, СКНФ, метод Квайна

Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Особо место среди этих представлений занимает совершенная ДНФ (СДНФ) и совершенная КНФ (СКНФ).

Пусть () – набор логических переменных, - набор нулей и единиц.

Определение

Конституентой единицы набора называется конъюнкт .

Конституентой нуля называется дизъюнкт .

Отметим, что , а тогда и только тогда, когда .

Определение

Совершенной ДНФ называется дизъюнкция некоторых конституент 1, среди которых нет одинаковых.

Совершенной КНФ называется конъюнкция некоторых конституент 0, среди которых нет одинаковых.

Таким образом, СДНФ (СКНФ) есть ДНФ (КНФ), в которой в каждый конъюнкт (дизъюнкт) каждая переменная из набора () входит ровно один раз, причем входит либо сама , либо ее отрицание .

Пример

Для произвольной булевой функции

Формула - конституента 1 - .

Формула - конституента 0 - .

Формула - СДНФ, формула -СКНФ.

Для решения задачи нахождения СДНФ и СКНФ эквивалентных исходной формуле , предварительно рассмотрим разложение булевой функции по к переменным, для определенности по , переменным) – разложение Шеннона.

Теорема

Любая булева функция представима в виде разложения Шеннона:

Доказательство

Прежде всего отметим, что тогда и только тогда, когда . Число всех наборов будет равно . Разобьем это множество на два класса: - некоторый фиксированный набор и оставшихся. Подставим вместо переменных значения фиксированного набора: , тогда левая часть формулы равна: , а правая часть: ==, то есть получили равенство левой и правой части. Рассмотрим оставшиеся наборов . Для каждого набора найдется хотя бы одна переменная , для которой . Следовательно, на каждом из этих наборов . Используя закон нуля: , получаем, что левая и правая часть равны при любой подстановке . Доказали справедливость для произвольного набора , значит справедливо для любого.

Теорема

Любая булева функция представима в виде разложения Шеннона:

Доказательство

Аналогично предыдущему.

В предельном случае, когда для булевой функции тождественно не равной 0, получаем ее представление в виде СДНФ:

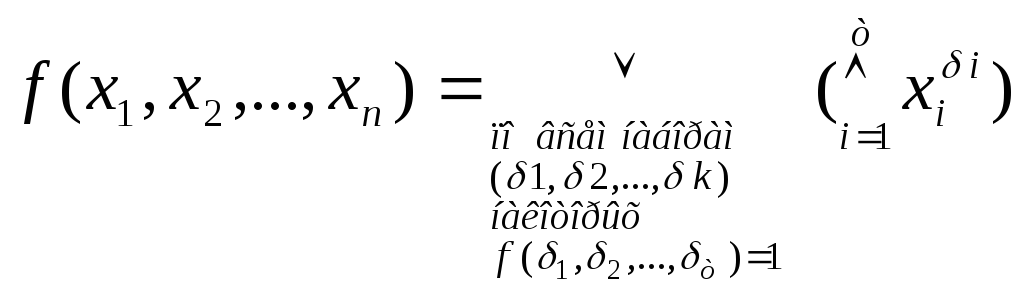
Аналогично для булевой функции тождественно не равной 1, получаем ее представление в виде СКНФ: .

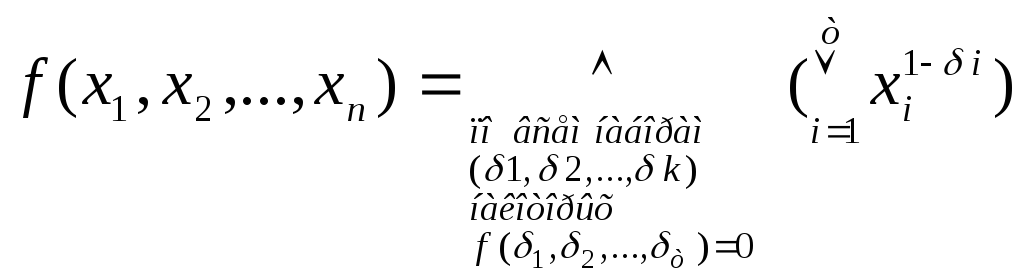Теорема

О функциональной полноте

Для любой булевой функции найдется формула , представляющая функцию .

Если тождественно не равна 0, то существует представляющая ее формула, находящаяся в СДНФ, и такое представление единственно с точностью до порядка следования конституент 1.

Если тождественно не равна 1, то существует представляющая ее формула, находящаяся в СКНФ, и такое представление единственно с точностью до порядка следования конституент 0.

Таким образом, любая булева функция может быть представлена формулой, использующей только операции дизъюнкции, конъюнкции и отрицания.

Пример

Найдем СДНФ и СКНФ для функции , заданной таблицей истинности:

0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

СДНФ:

СКНФ:

Минимизация булевых функций

Задача минимизации заключается в том, заданной булевой функции найти ДНФ, представляющую эту функцию и содержащую наименьшее число литералов.

Пример

Данная функция содержит 6 литералов. Возникает вопрос можно ли уменьшить это число?

Определение

Элементарную конъюнкцию называют импликантой булевой функции , если из того, что К=1 следует, что =1.

То есть, К- импликанта булевой функции , если .

Пример

импликанта булевой функции =

Определение

Элементарную конъюнкцию К называют простой импликантой булевой функции , если К является импликантой функции , из того, а элементарная конъюнкция, получаемая из К удалением любого литерала не будет импликантой.

Пример

Найдем все импликанты функции .

С переменными и мы можем составить всего 8 элементарных произведений. Ниже приведены их таблицы истинности:

x	y								x	y
0	0	1	1	0	0	0	1	1	0	0
0	1	1	0	1	0	0	1	0	0	1
1	0	0	0	0	1	0	0	1	1	0
1	1	1	0	0	0	1	0	0	1	1

Из таблицы истинности заключаем, что ,,,,y - импликанты нашей функции. Из них простыми импликантами являются ,y.

Определение

Сокращенная ДНФ - это дизъюнкция всех простых импликант булевой функции.

Теорема

Любая булева функция, не являющаяся константой 0, представима в виде сокращенной ДНФ.

Для нашего примера сокращенная ДНФ функции - .

Рассмотрим метод Квайна для нахождения сокращенной ДНФ для заданной функции. Определим три операции:

1. полного склеивания:

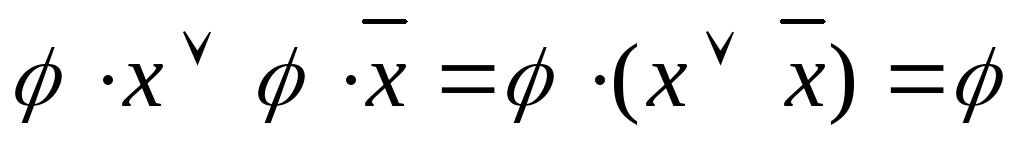
2. неполного склеивания:

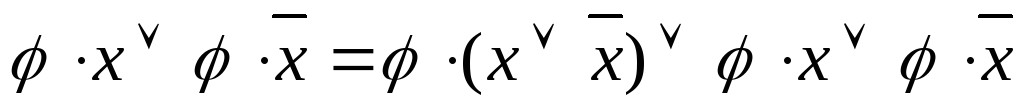
3. элементарного поглощения:

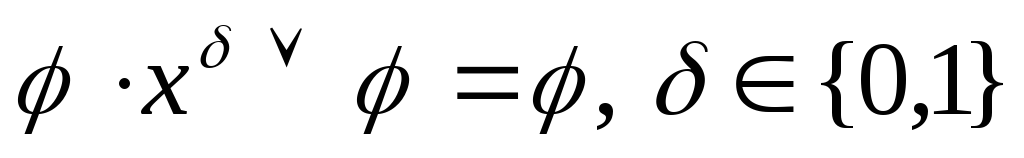
Теорема Квайна

Если исходя из СДНФ, произвести все возможные операции неполного склеивания, а затем элементарного поглощения, то в результате получиться сокращенная ДНФ, то есть дизъюнкция всех простых импликант.

На практике при выполнении операций неполного склеивания на каждом этапе можно не писать элементы, участвующие в этих операциях, а писать только результаты всевозможных полных склеиваний и конъюнкты, не участвующие в таких склеиваниях.

Пример

Пусть функция задана СДНФ: =

(1) (2) (3) (4)

Произведем операции склеивания, а затем элементарного поглощения:

==

(1 и 2) (2 и 3) (3 и 4)

=

Подробно

=(1 + 2)== (2 + 3)

=

= =(3 +4)

=

=

Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицы истинности. Если из сокращенной ДНФ удалить все лишние импликанты, то получается ДНФ, называемая тупиковой. Представление функции в виде тупиковой ДНФ в общем случае неоднозначно. Выбор из всех тупиковых ДНФ формы с наименьшим числом литер дает минимальную ДНФ.

Для получения минимальной ДНФ используется матрица Квайна, которая строится следующим образом. В заголовках столбцов таблицы записываются конституенты 1 из СДНФ, а в заголовках строк – простые импликанты из полученной сокращенной ДНФ. В таблице звездочкой отмечаются те пересечения строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту 1, являющейся заголовком столбца.

Для рассмотренного ранее примера матрица Квайна имеет вид:

импликанты	конституенты единицы
	*	*
		*	*
			*	*

В тупиковую ДНФ выбирается минимальное число простых импликант, дизъюнкция которых сохраняет все конституенты единицы, то есть, каждый столбец матрицы Квайна содержит звездочку, стоящую на пересечении со строкой, соответствующей одной из выбранных импликант. В качестве минимальной ДНФ выбирается тупиковая, имеющая наименьшее число литералов.