Конспект ТФКЗ

G

0, що

G

z•0

R

• 0

f z M

Побудуємо в області D коло R :

	z z0	R, яке повністю належить області
	D, таке, щоб на ньому була хоча б одна
точка		0, яка не належить множині G. Це

завжди можна зробити, оскільки z0 – гранична точка множини G.

Тоді f 0 M і, в силу неперерв-

ності функції f z , для довільного достат-

G

ньо малого 0 на колі R завжди можна вказати такий окіл U 0 1, 2 точки

для z U 0 . За формулою (4.2)

2

1

2

2

2 M

f z

d

f z

d

f z

d

f z

d

0

0

1

2

M 1 M 2 1 M 2 2 2 M 2 1 2 M .

Ми прийшли до протиріччя. Отже, функція

f z

, яка відмінна від сталої,

досягає свого максимального значення у граничних точках області. ◄

3. Принцип мінімуму модуля аналітичної функції

Якщо

функція комплексної

змінної

w f z

аналітична в

області

D,

неперервна

в замкненій

області

,

не є

сталою

і

f z 0 для

z D,

то

D

min

f z

досягається на межі області

D або функція

f z

є постійною. (Для

доведення цього твердження достатньо побудувати

функцію z 1 f z і

застосувати до неї принцип максимуму модуля).

4. Якщо функції

комплексної

змінної f1 z ,

f2 z є аналітичними

у

замкненій області

D

, яка обмежена скінченою кількістю жорданових кривих,

то

з того, що f1 z f2 z для z D випливає, що f1 z f2 z для z D.

Розглянемо функцію z f1 z f2 z . Тоді z 0	для z D. Нехай
z0 – довільна внутрішня точка області D. Знайдемо

z0	1			d 0 f1 z0 f2 z0 .
	2 i	D z0

Оскільки z0 є довільною внутрішньою точкою області D, то f1 z f2 z

для z D.

61

f

§ 5. Похідні вищих порядків від аналітичної функції. Теореми Морера і Ліувілля. Інтеграли Коші та типу Коші

Теорема. Нехай функція w f z визначена і аналітична в однозв’язній об-

ласті D і неперервна в замкненій області D D D. Тоді у будь-якій точці z0 області D функція w f z має похідні довільних порядків, які визначаються за формулами

f n z0

n!

f

d .

(5.1)

2 i

z

0

n 1

Доведення.

D

z0

до межі D області

► Нехай 0

– віддаль від точки

D, і нехай

z

z0 z z0

. Тоді точка z0 z

є внутрішньою точкою області D і

для неї можна записати інтегральну формулу Коші

1

f z0 z 2 i D z0 z d .

Побудуємо різницеве відношення:

f

f z0 z f z0

1

1

1

1

f

d

z

z

2 i

z

z

z0

z0

D

f

1

1

f

z

d

1

d .

2 i

z

z

0

z z

0

2 i

z

0

z z

0

D

D

Покажемо,

що для

z 0

останній

вираз має

границю, яка

дорівнює

1

f

d . Для цього оцінимо різницю

2 i

z

2

D

0

1

f

1

f

Q

d

d

2 i

z0 z z0

2 i

z0

2

D

D

1

f

1

1

d

2

z0 z z0

2

D

z0

f

z

1

f

z0 z0 z

d

1

.

d

2

2

2

2

D

z0 z z0

D

z0

z0 z

Оскільки

z0

, то

1

1

, і

z0

2

2

1

1

z0 z

z0

z

z

.

z0 z

z

62

Внаслідок неперервності функції

f z маємо, що

f

M

на межі D. Тоді

Q

1

f

z

d

1

M

z

L, L

D

.

2

z0

z

2

2

D

z0

2

z

Якщо z 0, то Q 0. Це означає, що існує

lim

f z0 z f z0

1

f

d f z0 .

2 i

z

2

z 0

z

0

D

Отже, формула (5.2) справедлива для n 1.

Використовуючи метод математичної індукції, можна довести, що для

n N

f n z0 2n!i D fz0 n 1d . ◄

Отже, аналітична в області D функція f z має похідні довільного порядку, які є аналітичними функціями в області D.

Наслідки.

1. Теорема Морера (достатні умови існування первісної). Нехай функція

w f z неперервна в однозв’язній області		D і f d 0 для
довільного гладкого контуру D.	Тоді	функція w f z є
аналітичною в області D.
Доведення.	f z і довільних внутрішніх
► За виконання умов теореми для функції
z

точок z0, z D існує первісна F z f d , яка є аналітичною в області D, і

z0

f z . А похідна від аналітичної функції є аналітичною функцією в

існує F z

області D, тобто для z

D існує F

f

z

z , що і доводить теорему. ◄

2. Теорема

Ліувілля.

Нехай

функція

w f z

є

аналітичною у всій

комплексній площині, а її модуль рівномірно обмежений. Тоді

функція w f z є тотожньо стала.

Доведення.

f z є аналітичною і

f z

M .

► За умовою теореми для z C

функція

Нехай де R :

z

R – коло радіуса R. Оцінимо

1

f

1

f

1 M

M

f z

2d

2

d

2

2 R .

2 i

z

2

z

2

R

R

R

R

63

Це означає, що при R		0 незалежно від вибору точки z. Звідси
	f z
випливає, що для z C похідна			z 0		f z const . ◄
		f

§ 6. Інтеграли Коші та типу Коші

Нагадаємо, що інтегральна формула Коші (4.1)

f z0	1		f		d	(6.1)
	2 i		z	0

дозволяє знайти значення аналітичної функції f z у точці z0 через її значення на довільному замкненому контурі, який охоплює точку z0 і належить області аналітичності. Інтеграл у правій частині (6.1) називають інтегралом Коші.

Нехай f z – аналітична у деякій області D, – межа області D, z – довільна точка комплексної площини, яка належить області D. Тоді справед-

лива формула Коші

f z	1		f	d ,	(6.2)
	2 i
			z

Інтеграл у правій частині формули (6.2) називають інтегралом типу Коші. Ця формула дозволяє знайти значення функції f z через її значення на межі цієї області. Інтеграл Коші є частинним випадком інтеграла типу Коші, якщо контурє замкненим, а функція f z – аналітичною в області, що містить в собі повністю контур інтегрування.

Запишемо подібний інтеграл для довільної функції f z , визначеної і неперервної на кусково-гладкій кривій (замкненій або незамкненій):

Φ z	1		f	d .	(6.3)
	2 i
		Γ	z

Інтеграл типу Коші (6.3) визначає однозначну функцію Φ z у всіх точках z, які не лежать на кривій . Якщо є замкненою кривою, а функція f z – аналітичною всюди всередині замкненої області, обмеженої кривою , то вираз (6.3) перетворюється на формулу Коші (6.1).

Теорема. Нехай Γ C – кусково-гладка крива, а f z – неперервна на кривій

Γ функція. Тоді функція Φ z				(6.2) є аналітичною у будь-якій області
D комплексної площини,		яка не містить точок кривої Γ , нескінченно
диференційованою в області D і
Φ n z	n!			f	d , n N .
	2 i			n 1
		Γ	z

64

ЛЕКЦІЯ 6

Ряди у комплексній площині

§ 1. Числові ряди. Збіжність. Ознаки збіжності. Абсолютна збіжність

	Нехай	задано	числову послідовність		комплексних чисел zn , n N,
zn xn iyn.
	Числовим рядом у комплексній площині називають вираз виду
			zn z1 z2 ... zn ....							(1.1)
			n 1
	Ряд (1.1) називається збіжним, якщо числова послідовність Sm частин-
		m
них сум Sm zn			є збіжною. Границю		S lim Sm					називають сумою ряду
		n 1				m
				m		m
(1.1). Оскільки Sm ReSm iImSm xn					i yn , то для збіжності ряду (1.1)
				n 1	n 1
необхідно і		достатньо,		щоб збігалися числові ряди,						побудовані з дійсних
xn та уявних yn частин.
n 1		n 1
	Ряд
				rm zn						(1.2)
				n m 1
називають m-им залишком числового ряду (1.1)
	Якщо ряд (1.1) є збіжним, то S Sm rm і для
				0 N : m N			rm		.

Критерій Коші (необхідна і достатня умова збіжності числового ряду):

			0 N N : m N, p 0	m p
	lim Sm S			zn	, (1.3)
	m			n m 1

Це прямий наслідок критерію Коші для збіжної числової послідовності.

Необхідною умовою збіжності числового ряду (1.1) є умова

lim zn 0.

n

Справді, якщо існує S lim Sm, то внаслідок виконання критерію Коші (для

m

p 1)

0 N : n N zn 1 Sn 1 Sn ,

65

звідки випливає, що lim

zn

0

lim zn 0.

n

n

Числовий ряд

(1.1)

називають

абсолютно збіжним,

якщо збігається

числовий ряд

zn

,

побудований з абсолютних величин zn.

Якщо числовий

n 1

ряд (1.1) є абсолютно збіжним, то він є і збіжним, але не навпаки.

m p

m p

Справді,

з нерівності

zn

zn

випливає, що якщо виконується

n m 1

n m 1

критерій Коші для ряду zn , то критерій Коші виконується і для ряду (1.1).

n 1

Якщо ряд (1.1) є збіжним, а ряд zn – розбіжним, то кажуть, що ряд

n 1

(1.1) є умовно збіжним.

Оскільки ряд zn є рядом з додатними членами, то для дослідження

n 1

його на збіжність використовують всі ознаки збіжності рядів з додатними членами: ознаку порівняння, ознаку Даламбера, ознаку Коші.

Приклад 1. Дослідити на збіжність ряд ein .

n 1

• Оскільки zn ein cosn isinn, то дослідимо на збіжність ряди cosn

n 1

і sinn. Для послідовностей cosn , sinn не виконується необхідна умова

n 1

	збіжності ряду. Тому ряди cosn і	sinn	є розбіжними, а значить і ряд
	n 1	n 1
	ein є розбіжним. •
	n 1			nsin in
	Приклад 2. Дослідити на збіжність ряд zn,		zn		.
		n 1		3n

• Дослідимо ряд на абсолютну збіжність. Враховуючи, що sin iz i sh z , маємо

nsin in

n sh n

nsh n

nen

e n

zn

n

.

3n

3n

3n

3n

3

66

За ознакою Даламбера	lim
	n

n 1 e n 13

e n n 3

	e				e			n
			1, тобто ряд	n					є
						3
3				n 1

	nsh n
збіжним, отже, за ознакою порівняння ряд				є також збіжним. Отже, ряд
	3	n
n 1

nsin in збігається абсолютно і є збіжним рядом. •

n 1 3n

Збіжні числові ряди в комплексній площині володіють всіма властивостями збіжних числових рядів з дійсними членами.

§ 2. Функціональні ряди. Область збіжності. Рівномірна збіжність. Властивості рівномірно збіжних функціональних рядів

Нехай в області D визначено функціональну послідовність n z однозначних функцій комплексної змінної n z .

Функціональним рядом називають вираз

	n z .		(2.1)
	n 1	z0 D ряд (2.1)
Очевидно,	що для всіх фіксованих		перетворюється у
числовий ряд (1.1). Функціональний ряд (2.1) називають збіжним в області D,
якщо для z0	D відповідний йому	числовий ряд є	збіжним. Якщо

функціональний ряд є збіжним в області D, то в цій області можна означити однозначну функцію f z , значення якої в кожній точці z0 D дорівнює сумі

відповідного числового ряду, тобто n z0 f z0 . Це означає, що для

n 1

n

z D 0 N N : n N f z k z .

k 1

Область D називають областю збіжності функціонального ряду.

Як і на множині дійсних чисел, важливе місце в теорії функцій комплексної змінної займає поняття рівномірної збіжності.

Функціональний ряд (2.1) рівномірно збігається до своєї суми

				в області D тоді і тільки тоді, коли
	n z		f z
n 1

67

				n
0 N N : n N z D		f z k z						(2.2)
або				k 1
	N N : n N z D			rn z
0						,		(2.3)

де rn z k z – залишок функціонального ряду.

k n 1

Теорема 2.1. Для того, щоб функціональний ряд (2.1) був збіжним (рівномірно збіжним) в області D до своєї суми f z , необхідно і достатньо, щоб в

області D були збіжними (рівномірно	збіжними)	до функцій
u Re f z , v Im f z функціональні ряди	un x, y і	vn x, y , де
un x, y Re n z , vn x, y Im n z .	n 1	n 1

Використовуючи означення збіжності (рівномірної збіжності) функці-

онального ряду і нерівності

Rez

z

Rez

Imz

,

Imz

z

Rez

Imz

,

теорема легко доводиться.

Достатня ознака збіжності функціонального ряду

Теорема 2.2 (ознака Вейєрштрасса). Функціональний ряд (2.1) збігається в області D рівномірно та абсолютно, якщо існує збіжний числовий ряд

an з додатними членами такий, що

n 1

n N z D			n z				an.		(2.4)
Доведення.
► За умовами теореми ряд an	збігається:
n 1
z D 0 N0 : n N0								ak .
		n z			an,			k n 1	області D для
Внаслідок рівномірної оцінки								всюди в

n N0 виконується нерівність

k k ak ,

k n 1 k n 1 k n 1

а це означає, що ряд (2.1) є абсолютно і рівномірно збіжним. ◄

Ряд an називають мажорантою ряду (2.1).

n 1

68

Необхідна і достатня ознака збіжності функціонального ряду

Теорема 2.3 (критерій Коші). Для того, щоб функціональний ряд (2.1) збі-гався рівномірно в області D, необхідно і достатньо, щоб

0 N0 : n N0, m N z D Sn m z Sn z . (2.5)

Властивості рівномірно збіжних рядів

1. Теорема 2.4. Нехай функції n z неперервні в області D, а ряд (2.1) рівномірно збігається в області D до своєї суми f z . Тоді функція f z є неперервною в області D.

Доведення.

►Оскільки ряд n z f z , то

n 1

0 N0 : n N0 z D

n

f z k z

.

k 1

Нехай

z0 – довільна точка області D. Виберемо значення

n

настільки

n

великим, щоб в області

D для частинної суми Sn z k z

виконувалася

f z S

z

k 1

z – не-

нерівність

n

, і зафіксуємо це значення

n. Сума

S

n

3

що для всіх z,

перервна в

D, а тому існує таке значення 0,

які задоволь-

няють умову

z z

0

, виконується нерівність

S

n

z S

n

z

0

.

3

Тоді

f z f z0 f z Sn z Sn z Sn z0 Sn z0 f z0

f z Sn z Sn z Sn z0 Sn z0 f z0 3 3 3 . ◄

2. Теорема 2.5. Нехай функції n z є неперервними в області D, D – довільний кусково-гладкий контур, а ряд (2.1) рівномірно збіга-ється в області D до своєї суми f z . Тоді

f z dz n z dz,		(2.6)
	n 1

Доведення.

69

n

► Нехай n k z dz Sn z dz – частинна сума проінтегрова-ного

k 1

ряду.

Покажемо,

що

lim n f z dz.

Оскільки

для

z D ряд

n

n z

f z , то для

n 1

: n N

z D

f z S

z

0 N

0

0

n

, де L

.

L

Для n N0 маємо

f z dz n

f z Sn z dz

f z Sn z

dz

L L .◄

Зауважимо, що властивості 1 і 2 рівномірно збіжних рядів функцій комплексної змінної аналогічні до відповідних властивостей на множині дійсних функцій.

Найважливішою властивістю рівномірно збіжних рядів є теорема Вейєрштрасса.

3. Теорема 2.6 (перша теорема Вейєрштрасса). Нехай функції n z аналі-

тичні в області D, а ряд (2.1) рівномірно збігається у довільній замкненій підобласті D до своєї суми f z . Тоді

1) функція f z є аналітичною в області D;

2) f k z nk z ;

n 1

3) ряд nk z є рівномірно збіжним у замкненій підобласті .

n 1

Доведення.

► 1) Нехай D D – довільна однозв’язна область. За властивістю 1 (теорема 2.4) функція f z , яка є сумою функціонального ряду (2.1), буде неперервною в області D . Нехай D – довільний замкнений гладкий контур. За властивістю 2 (теорема 2.5) існує

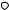f z dz 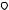n z dz.

n 1

Функції n z аналітичні для		z D,	а, отже, і	для z D . Тому за
теоремою Коші n z dz 0		f z dz	0. Отже,	за теоремою Морера

70