Учреждение образования «высший государственный колледж связи»

кафедра М и Ф

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

«Обшая теория статистики»

для студентов уровня ВО заочной формы обучения

специальностей

1-26 02 03 – Маркетинг

1-25 01 07 – Экономика и управление на предприятии

Минск 2007

Составитель Е.М. Колодная

Рецензент Л.Л. Гладков

Издание утверждено на заседании кафедры М и Ф

«20» марта 2007 г., протокол №8

Зав. кафедрой Л.Л. Гладков

Литература

1. Елисеева И. И., Юзбашев М. М. Общая теория статистики. – М.: Финансы и статистика, 2001.

2. Ефимова М. Р., Петрова Е. В., Румянцев В. Н. Общая теория статистики. – М.: ИНФРА-М, 1997.

3. Ряузов Н. Н. Общая теория статистики. – М.: Финансы и статистика, 1984.

4. Гусев Н. Ю. Статистика: основы методологии: Учебное пособие. – М.: Издательство АСВ, 1998.

5. Сиденко А. В., Попов Г. Ю., Матвеева В. М. Статистика: Учебник. – М.: Дело и Сервис, 2000.

1 Ряды распределения. Средние величины. Показатели вариации и другие характеристики рядов распределения. Статистические графики

1.1 Построение рядов распределения

Ряд распределения - упорядоченное распределение единиц совокупности на группы по какому-либо варьирующему признаку. Имеет два элемента: варианты (значение группировочного признака) и частоты (число единиц с данным вариантом). В атрибутивных рядах варианты выражаются словом, а в вариационных - числом.

Вариационные ряды распределения делятся на:

- дискретные (в качестве вариант выступают дискретные числа);

- интервальные (в качестве вариант выступают числовые интервалы).

Для построения дискретного ряда распределения необходимо перечислить все наблюдаемые значения признака (варианты) в порядке возрастания их числовых значение и соответствующие им частоты.

Для построения интервального ряда распределения необходимо записать последовательность интервалов и соответствующие им частоты (в качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал).

При построении интервальных вариационных рядов распределения предварительно требуется решить вопрос относительно:

а) числа образуемых групп;

б) интервалов групп.

Однозначного ответа на вопрос о числе групп нет. Самый простой ответ - число групп не должно быть слишком большим (не более 15-16) и слишком малым (не менее 3-х). Чаще оптимальным является число 5-6. Математическое правило определения числа групп выражается формулой:

,

где - число групп;

- число единиц совокупности.

Интервалы различают равные и неравные. Величина равного интервала определяется по формуле:

,

где - размер интервала;

- максимальное значение признака;

- минимальное значение признака;

- число образуемых групп.

1.2 Средние величины

Средней величиной называют обобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу совокупности в конкретных условиях места и времени.

Существует два класса средних - степенные и структурные.

К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и средняя кубическая.

Средняя арифметическая:

простая

;

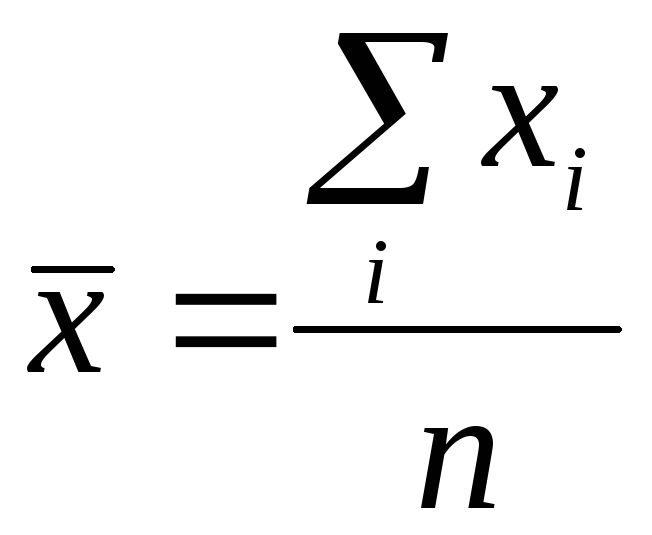взвешенная

,

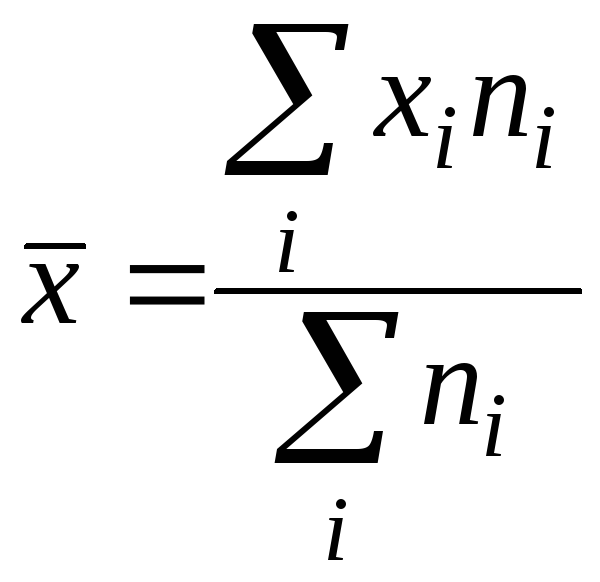где - веса (или частоты), показывающие число одинаковых значений признака (вариант).

Для расчета средней арифметической в интервальном ряду распределения, его необходимо преобразовать в дискретный ряд. За дискретное число принимают простую арифметическую среднюю из нижнего и верхнего значений интервала. Если первый или последний интервал открытые - их предварительно закрывают, т.е. находят в первой группе начальное значение интервала, а в последнем - верхнее значение интервала. При этом обычно применяется такой способ: для первой группы весь интервал принимается равным величине интервала второй группы, для последней группы длина интервала берется в соответствии с величиной интервала предпоследней группы.

Пример 1.1

По строительным предприятиям области получены данные об объеме выполненных строительных работ за год (см. табл. 1.1).

Таблица 1.1

Группы пред- приятий по объему выпол- ненных работ, млн. руб.	Число предприя- тий (n)	Расчетные показатели
		закрытые интервалы по группам	центральное значение интервала ()	xn
до 500	8	300-500	400	3200
от 500 до 700	12	500-700	600	7200
от 700 до 1000	6	700-1000	850	5100
свыше 1000	4	1000-1300	1150	4600
Итого:	30	—	—	20100

Вычислим средний объем выполненных работ на одно предприятие, используя формулу средней арифметической взвешенной.

Вначале закрываем интервалы. Исходя из того, что весь интервал второй группы равен 200, нижняя граница первого интервала будет исчислена: 500-200=300. Интервал предпоследней группы равен 300, тогда верхняя граница последнего интервала будет 1000+300=1300. В графе 3 все интервалы после этих расчетов записаны закрытыми. По формуле простой арифметической средней исчисленные центральные значения интервалов записаны в графе 4. Эти значения и будут служить вариантами () для расчета средней арифметической взвешенной

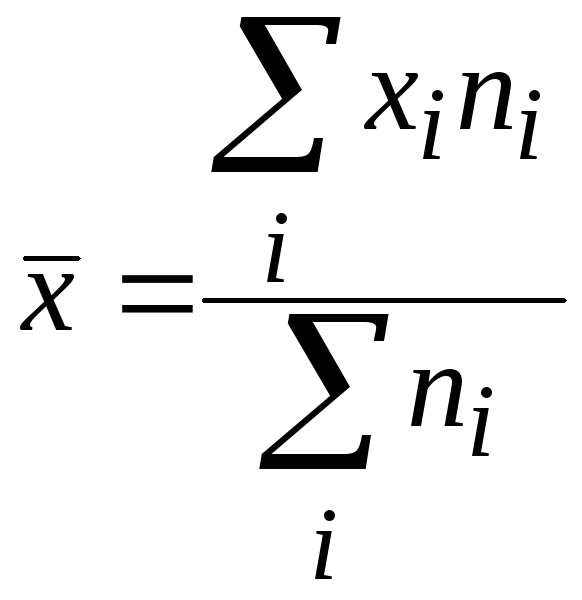==670 (млн. руб.).

Средняя гармоническая:

простая

;

взвешенная

,

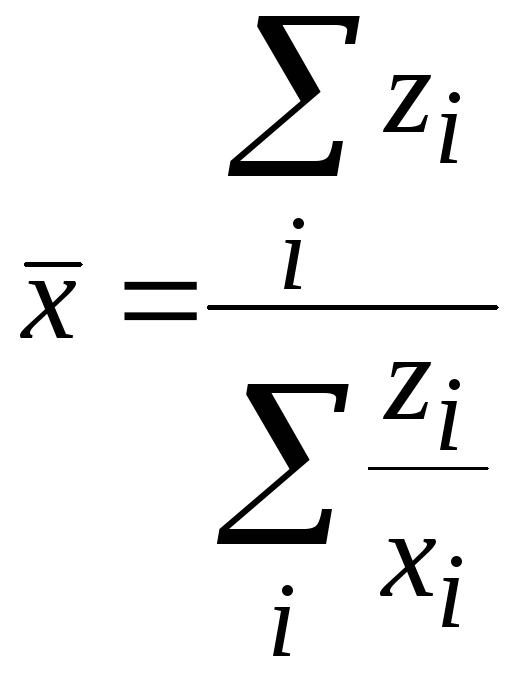где .

Приведем пример расчета средней гармонической. Допустим, что трое рабочих работали по 8 часов (480 мин.) и затрачивали на отделку 1 кв. м стен: 1-й – 30 мин., 2-й – 40 мин., 3-й – 60 мин. Найти среднюю затрату времени на отделку 1 кв. м стен по формуле:

.

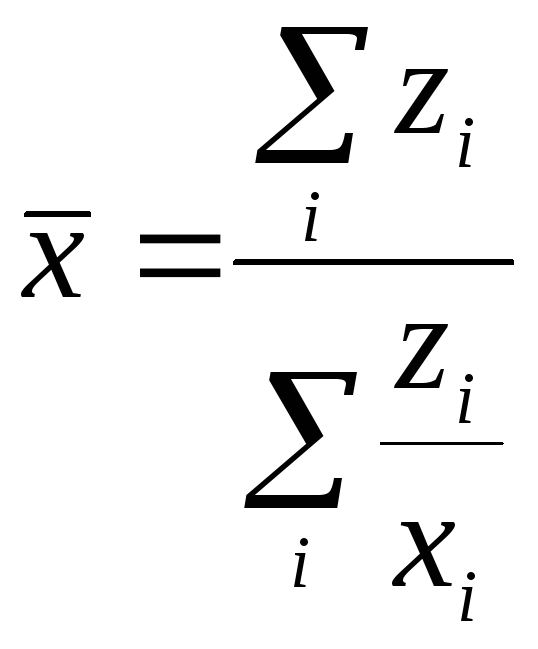
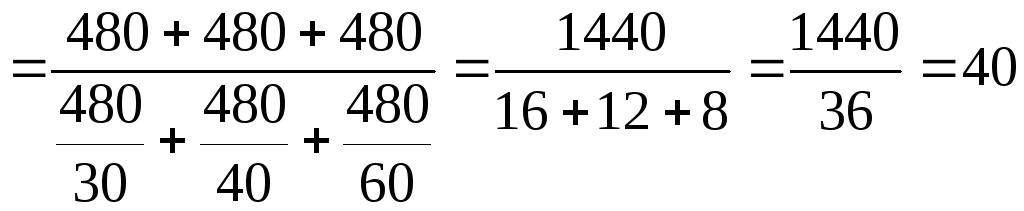В этом расчете в числителе значится общее время работы трех рабочих (1440 мин.), а в знаменателе общее количество отделанных кв. м (36 кв. м). Средняя затрата времени на отделку 1 кв. м составляет 40 мин. В данном примере веса средней равные и поэтому можно записать:

.

Следовательно, при равных весах расчет может быть произведен по формуле:

.

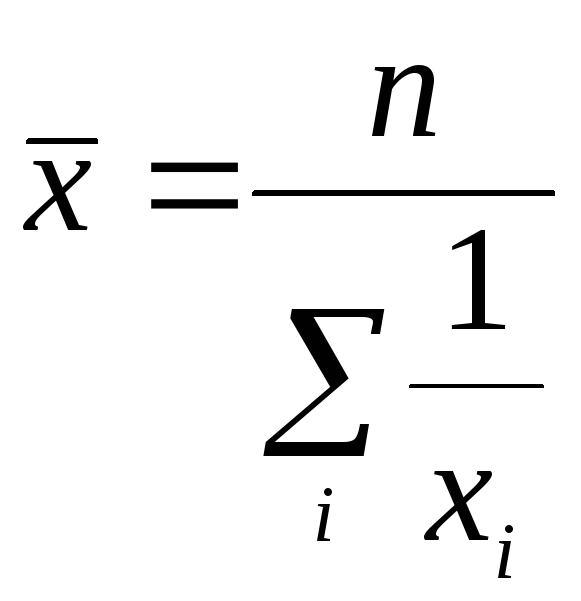Средняя квадратическая:

простая

;

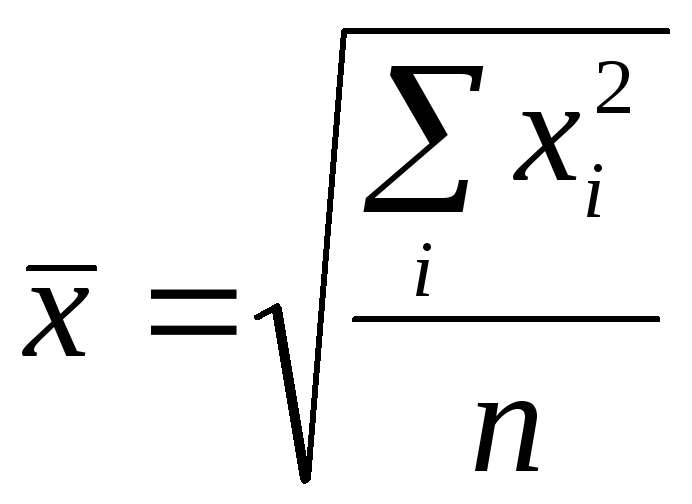взвешенная

.

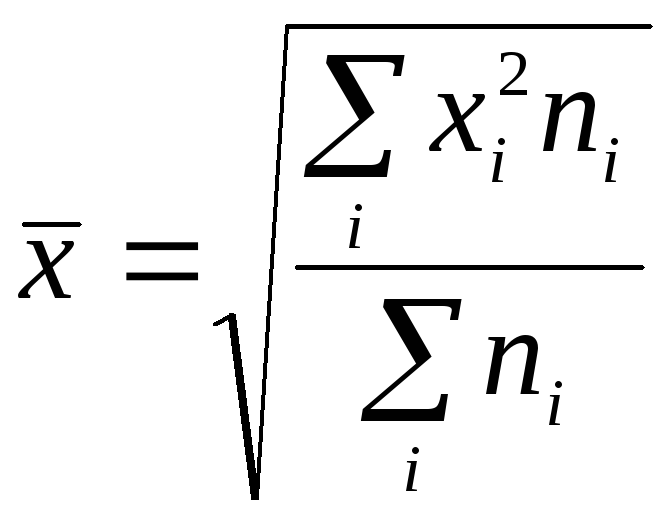Эта средняя применяется при нахождении показателей вариации, которые рассматриваются далее, например, среднеквадратического отклонения.

Средняя геометрическая:

,

Эта средняя применяется, например, при нахождении средних темпов роста в рядах динамики.

К структурным средним относятся мода и медиана.

Мода - это величина признака (вариант), который чаще всего встречается в данной совокупности.

В дискретном ряду распределения моду исчислять не требуется, она находится как значение варианта (), у которого наибольшая частота ().

Пример 1.2

Имеется следующий ряд распределения семей по числу членов семьи:

Таблица 1.2

Число членов семьи ()	2	3	4	5	6
Число семей ()	300	500	260	100	40

Здесь мода =3 человека в семье, так как наибольшее число семей (500) в данном ряду имеют 3 человека в семье.

В интервальном ряду мода определяется по формуле:

,

где - мода;

- начальное значение модального интервала (интервала, содержащего наибольшую частоту);

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному интервалу;

- частота интервала, следующего за модальным интервалом.

Рассмотрим нахождение моды в интервальном ряду распределения по условию табл. 1.1.

В этой задаче наибольшая частота (12) находится в интервале от 500 до 700. Это модальный интервал. Тогда мода:

.

Итак, модальная величина объема выполненных работ составляет 580 млн. руб.

Медиана - это вариант, расположенный в середине ранжированного (упорядоченного) ряда.

Ранжированным называется ряд, в котором единицы совокупности расположены в возрастающем (или убывающем) порядке значений варианта.

В дискретном нечетном (нечетное число единиц) вариационном ряду распределения медианой будет значение - го варианта.

Например, при испытании прочности семи образцов стекла на силу удара в кг были получены результаты:

4, 5, 6, 7, 8, 8, 15.

В середине ранжированного ряда находится четвертый вариант и его величина есть медиана. Итак, кг или медианное значение прочности стекла при испытании на силу удара составило 7 кг.

В дискретном четном (четное число единиц) вариационном ряду распределения медиана находится как средняя из двух вариантов, расположенных в середине ранжированного ряда, т.е. среднее значение - го и- го вариантов.

Рассмотрим нахождение медианы в дискретном четном ряду распределения по условию табл. 1.2. Данный ряд имеет четное число элементов, так как

300+500+260+100+40=1200, тогда в середине ранжированного ряда будут находиться -ый и ()-ый варианты, или 600-ый и 601-ый. По суммам накопленных частот (см. табл. 1.3) видно, что и 600-ый и 601-ый варианты имеют значение 3. Значит медиана=3 человека в семье.

Таблица 1.3

Число членов семьи ()	2	3	4	5	6
Число семей ()	300	500	260	100	40
Сумма накопленных частот (S)	300	800	1060	1160	1200

Медиана интервального вариационного ряда определяется по формуле:

,

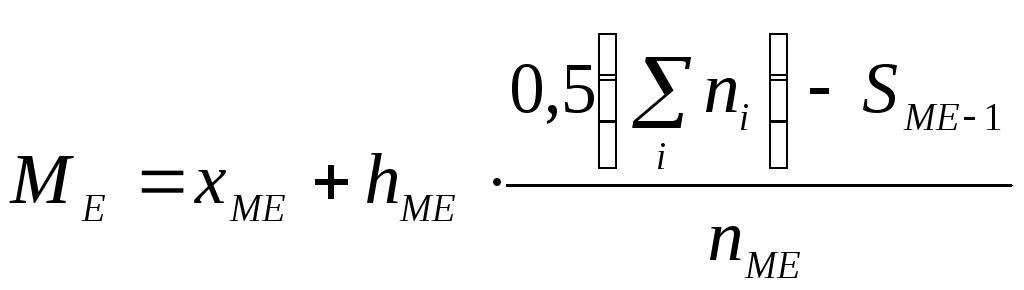- начальное значение медианного интервала (интервала, содержащего медиану);

- величина медианного интервала;

- сумма частот ряда;

- сумма накопленных частот, предшествующих медианному интервалу;

- частота медианного интервала.

По данным табл. 1.1 найдем медиану.

Таблица 1.4

Группы предприятий по	Число	Сумма накопленных
объему выполненных	предприятий	частот
работ, млн. руб.	(n)	(S)
От 300 до 500	8	8
От 500 до 700	12	20
От 700 до 1000	6	26
От 1000 до 1300	4	30
Итого:	30	—

В данном примере в середине ряда находится варианты с порядковыми номерами 15 и 16. Медианным интервалом является второй – от 500 до 700.

Находим медиану по приведенной выше формуле.

.

Итак, медиальная величина объема выполненных работ составляет 617 млн. руб.