1. Основные сведения из теории вероятностей и математической статистики

1.1. Основные понятия

Математическая статистика – специальная наука, занимающаяся разработкой методов регистрации, обработки и анализа статистических данных, получаемых в результате наблюдения массовых случайных явлений. Математической основой этой науки является теория вероятностей.

Событие – всякий факт, который может произойти или не произойти в результате опыта.

Вероятность события 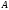(математическая вероятность) – отношение числа случаев, благоприятствующих событию 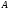, к общему числу случаев: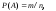где- число случаев, благоприятствующих событию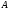;- общее число случаев.

Частота события в данной серии опытов (статистическая вероятность) – отношение числа опытов, в которых появилось событие , к общему числу произведенных опытов: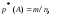где- число опытов, в которых появилось событие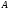;- общее число произведенных опытов.

При большом числе опытов частота события сходится по вероятности к вероятности события в отдельном опыте (закон больших чисел).

Случайная величина (СВ) – такая величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестно, какое именно. Случайная величина может быть дискретной (ДСВ) и непрерывной (НСВ). Случайная величина, принимающая только отделенные друг от друга значения, которые можно заранее перечислить, называется дискретной. Примеры ДСВ: год постройки, срок эксплуатации, количество изделий. Примеры НСВ: площадь, стоимость единицы площади, время, масса отдельно взятой детали.

Законы распределения СВ. Законом распределения СВ называют всякое соотношение, устанавливающее связь между возможными значениями СВ и вероятностями этих значений. Простейшей формой задания закона распределения СВ является статистический ряд, т.е. таблица 2.1, в которой перечислены возможные значения СВ и соответствующие им вероятности.

Т а б л и ц а 1.1

Статистический ряд

Графическое изображение статистического ряда называется многоугольником распределения (рис.1.1). Ряд распределения и многоугольник распределения существуют только для ДСВ.

Для непрерывных СВ существует понятие плотность распределения, характеризующая как бы плотность, с которой концентрируются и распределяются значения СВ в данной точке. Кривая, изображающая плотность распределения, называется кривой распределения (рис.1.2).

Рис.1.1. Многоугольник Рис.1.2. Плотность

распределения распределения

Основные свойства кривой распределения:

• т.е. вся кривая расположена выше оси 0х;

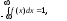• т.е. площадь под кривой равна 1.

Генеральная совокупность (статистическая совокупность) – множество объектов одного и того же вида или множество значений какого-либо признака объекта.

Случайная выборка (выборка) – совокупность случайно отобранных объектов наблюдения из генеральной совокупности.

Часто для исследования СВ при постоянных условиях проводят испытания. Множество полученных значений также называют выборкой и обрабатывают ее статистически, т.е. определяют закон распределения, числовые характеристики и пр.

Каждый отдельный объект выборки представляет собой элемент (единицу) совокупности, а общее число элементов – объем выборки. Например, известны значения влажности досок в штабеле: 19,8; 17,4; 18,3; 19; 18,9 %. Здесь объем выборки .

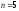Каждый элемент выборки характеризуется одним или несколькими признаками. Признаки могут быть количественными и качественными. Качественный признак - признак, характеризующий некоторое свойство или состояние наблюдаемой единицы выборки. Количественным признаком является признак, значения которого выражаются числами. Количественные признаки могут быть дискретными (ДКП) и непрерывными (НКП).

ДКП – признак, принимающий только отделенные друг от друга значения, как правило, целочисленные. НКП – признак, принимающий любые числовые значения в определенных пределах.

К особой группе признаков относятся ранговые признаки (показатели). Их значения устанавливаются путем упорядочения (ранжирования) единиц выборки в соответствии с некоторым признаком. Каждому элементу упорядоченного ряда присваивают некоторое число (обычно порядкового номера), называемого рангом.

Для учета в расчетах качественных признаков необходимо их ранжировать. Например, местоположение объекта недвижимости можно учитывать, присвоив следующие номера:

• центр города – 4;

• вблизи центра – 3;

• середина города – 2;

• окраина – 1.

Числовые характеристики СВ:

• математическое ожидание

• для ДСВ – это сумма произведений всех возможных значений СВ на вероятности этих значений

т.е. математическое ожидание определяется аналогично координатам центра масс.

• математическое ожидание для НСВ выражается определенным интегралом

Каждой числовой характеристике СВ соответствует ее статистическая аналогия, которая является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра – определенная числовая характеристика, полученная на основе выборки. Для математического ожидания такой аналогией является среднее арифметическое всех возможных значений СВ. Эту характеристику называют статистическим средним, выборочным средним или средним значением.

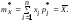
Так как при большом объеме статистического материала частота событий сходится по вероятности к вероятности события, то и выборочное среднее сходится по вероятности к математическому ожиданию СВ.

При малом числе наблюдений среднее наблюдаемых значений СВ определяется выражением:

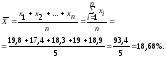
• центрированная СВ – разность между значением СВ и ее математическим ожиданием или отклонение СВ от ее математического ожидания

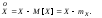
Размерность математического ожидания совпадает с размерностью СВ.

• дисперсия СВ - математическое ожидание квадрата соответствующей центрированной случайной величины:

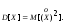
Для непосредственного вычисления дисперсии служат формулы:

• ДСВ -

• НСВ -

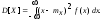
Если математическое ожидание является характеристикой положения СВ, то дисперсия характеризует разброс, рассеянность значений СВ около ее математического ожидания. Слово «дисперсия» означает рассеивание.

Аналогом дисперсии СВ является выборочная дисперсия

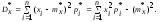
При малом числе наблюдаемых значений СВ вычисляют исправленную дисперсию

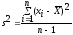при <30.

В знаменателе формулы стоит (-1) потому, что при малом объеме наблюдений среднее для выборки отличается от среднего генеральной совокупности. Здесь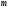=-1 – число степеней свободы, так как при расчете среднего была наложена одна связь:

.

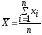• среднеквадратичное отклонение вводится в качестве характеристики рассеивания СВ, имеющей одинаковую размерность со случайной величиной:

.

Статистическими аналогами этой характеристики являются стандартные отклонения и

Статистической надежности в 95% соответствует доверительная вероятность – 0,95, а 5% задает уровень значимости 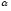или вероятность ошибки 0,05. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5%, т.е.<0,05. Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.

Числовые характеристики свойств распределения и связи, полученные на основе выборки, называются статистиками. Основной статистикой, характеризующей рассеяние СВ, является стандартное отклонение.

Кроме математического ожидания, на практике иногда применяются и другие характеристики положения, в частности мода и медиана случайной величины.

Модой СВ называется ее наиболее вероятное значение. Для непрерывной СВ модой является то значение, в котором плотность вероятности максимальна. На рис. 1.3 и 1.4 показана мода соответственно для дискретной и непрерывной случайных величин.

Рис. 1.3. Мода для ДСВ Рис.1.4. Мода для НСВ

Модой при малом числе наблюдений называют возможное значение СВ, которое имеет наибольшую абсолютную частоту. Например, для статистического ряда

	1	4	7	9
	5	1	10	3

мода равна 7.

Медианой случайной величины 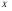называется такое ее значение, для которого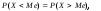т.е. одинаково вероятно, окажется ли случайная величина меньше или больше. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 1.5).

При малом числе наблюдений медианой называют возможное значение СВ, которое делит статистический ряд на две части. Если число возможных значений СВ нечетно, т.е. , то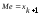. При четноммедиана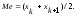

Коэффициент вариации или мера изменчивости представляет выраженное в процентах отношение стандартного отклонения к выборочному среднему

,

т.е. характеризует диапазон рассеяния значений СВ около среднего значения.

Рис. 1.5. Медиана для НСВ

Среднее значение и стандартное отклонение находят широкое применение при решении задач научного и практического характера. В частности, среднее значение можно использовать при оценке квалификации специалиста, а стандартное отклонение – при выяснении его способности сохранять постоянство качества своей работы.

Пример 1.1 [1]. Три сварщика изготовили по 100 опытных образцов из одних и тех же материалов для испытания на растяжение с целью выяснения механической прочности сварного шва. Требуется по результатам испытаний оценить квалификацию сварщиков и стабильность качества их работы.

Результаты испытаний и расчета в среде ЭТ представлены в таблице 1.2.

Т а б л и ц а 2.2

Результаты испытаний сварного шва и их обработка

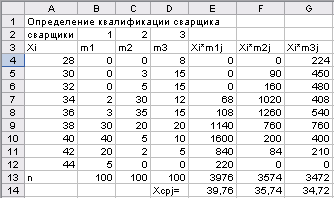
Продолжение таблицы 2.2

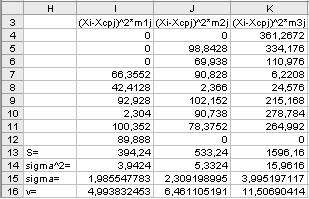
В таблице 1.2 обозначено: 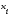- значение прочности сварного шва, МПа; 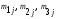_{- абсолютные частоты значений прочности сварного шва при испытании образцов первого, второго и третьего сварщиков;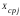} - средние значения прочности сварного шва, достигнутые сварщиками; sigma – стандартное отклонение и - коэффициент вариации значений прочности сварного шва для образцов каждого сварщика.

Расчетные формулы приведены в таблице 1.3.

Т а б л и ц а 1.3

Расчетные формулы

Адрес ячейки	Формула	Адрес ячейки	Формула
E4	=$a4*b4	I4	=($a4-e$14)^2*b4
E14	=e13/b13	B13	=СУММ(b4:b12)
I14	=i13/b13	I13	=СУММ(i4:i12)
I16	=i15*100/e14	I15	=КОРЕНЬ(i14)

Кривые распределения абсолютных частот значений прочности представлены на рис. 1.6.

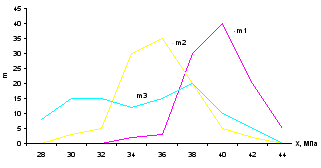
Рис.1.6. Кривые распределения абсолютных частот

Анализ результатов показывает:

• наилучшей квалификацией обладает первый сварщик, так как достигнутая им средняя прочность сварных швов равна 39,76 МПа, стандартное отклонение равно 1,985 МПа и коэффициент вариации -4,99%, что свидетельствует о постоянстве качества работы – малый диапазон разброса возможных значений прочности;

• наихудшей квалификацией и нестабильным качеством обладает третий сварщик, имеющий следующие значения аналогичных характеристик: средняя прочность – 34,72 МПа, стандартное отклонение – 3,995 МПа, коэффициент вариации – 11,507%

Абсолютная ошибка выборочного среднего позволяет по частному значению выборочного среднего судить о значении среднего генеральной совокупности и вычисляется по формуле

.

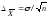При вычислениях каждая статистика должна учитывать абсолютную ошибку. Например, среднее значение прочности бетона равно

МПа.

Абсолютная ошибка стандартного отклонения вычисляется по формуле

.

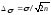Как видно из формул абсолютные ошибки статистик обратно пропорциональны корню квадратному из объема выборки. Следовательно, при достаточно большом числе наблюдений абсолютная ошибка становится настолько малой, что разность между статистиками и параметрами генеральной совокупности может не приниматься во внимание. В этом случае выборочные статистики могут использоваться вместо параметров генеральной совокупности.

Показатель точности исследования – это средняя ошибка, выраженная в %, т.е. относительная ошибка.

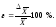
Чем меньше показатель точности, тем надежнее результаты исследований. Показатель точности не должен превышать принятого уровня значимости, т.е..

Если известен коэффициент вариации, то показатель точности исследования определяется по формуле

.

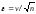Объем выборки при малом числе наблюдений рассчитывается по формуле

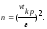
Пример 1.2. Имеется случайная выборка прочности бетона на сжатие в возрасте 28 суток: 24,8; 26,2; 28,1; 29,8; 30,4; 31,2; 32,2; 34,8; 35,8 МПа. Определить статистические параметры прочности бетона на сжатие.

Выборочное среднее

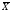=(24,8+26,2+28,1+29,8+30,4+31,2+32,2+34,8+35,8)/9=30,367 МПа.

Исправленная дисперсия

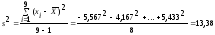
Стандартное отклонение

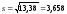МПа.

Коэффициент вариации

Средняя ошибка выборочного среднего

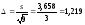МПа.

Показатель точности

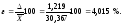
Объем выборки .

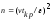Критическое значение - статистики определяем с помощью статистической функции СТЬЮДРАСПОБР мастера функций, диалоговое окно которой представлено на рис. 1.7.

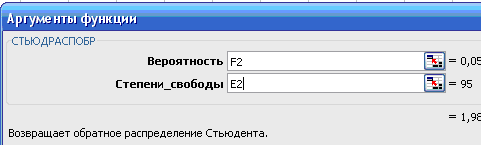
Рис. 1.7. Диалоговое окно функции СТЬЮДРАСПОБР

Результаты расчета данного примера в среде ЭТ приведены в таблице 1.4, расчетные формулы – в таблице 1.5.

Т а б л и ц а 1.4

Результаты расчета в среде ЭТ

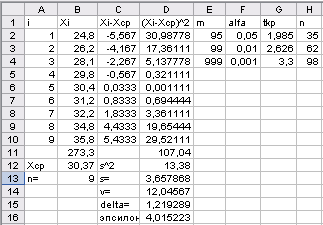
В таблице 1.4 дополнительно выполнен расчет объема выборок при различных уровнях значимости , который свидетельствует о том, что чем ответственнее испытания, тем больше должен быть объем выборки.

Т а б л и ц а 1.4

Расчетные формулы

Адрес ячейки	Формула	Адрес ячейки	Формула
B11	=СУММ(b2:b10)	D13	=КОРЕНЬ(d12)
B12	=b11/9	D14	=d13/b12*100
C2	=b2-$b$12	D15	=d13/КОРЕНЬ(b13)
D2	=c2^2	D16	=d15/b12*100
D11	=СУММ(d2:d10)	H2	=($d$14*g2/$d$16)^2
D12	=d11/(b13-1)	G2	=СТЬЮДРАСПОБР(f2;e2)