Функції

ЛЕКЦІЯ 11. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ. Ч. 2

11.1.Основні характеристики тригонометричних функцій

11.1.1.Синус

11.1.2.Косинус

11.1.3.Тангенс

11.1.4.Котангенс

11.2.Обернені тригонометричні функції

11.2.1.Означення обернених тригонометричних функцій

11.2.2.Формули значень тригонометричних функцій від обернених тригонометричних функцій

11.3. Основні характеристики обернених тригонометричних функцій

11.3.1.Арксинус

11.3.2.Арккосинус

11.3.3.Арктангенс

11.3.4.Арккотангенс

11.4. Основні тригонометричні рівняння й нерівності

11.4.1.Основні рівняння і нерівності з синусом

11.4.2.Основні рівняння і нерівності з косинусом

11.4.3.Основні рівняння і нерівності з тангенсом

11.4.4.Основні рівняння і нерівності з котангенсом

Короткий зміст

У цій лекції:

—означено обернені тригонометричні функції: арксинус, арккосинус, арктангенс та арккотангенс;

—розглянуто деякі співвідношення для цих функцій;

—подано основні характеристики і графіки тригонометричних і обернених тригонометричних функцій;

—вміщено методи розв’язання основних тригонометричних рівнянь і нерівностей.

2	Лекція 11. Тригонометричні функції. Ч. 2

11.1. Основні характеристики

тригонометричних функцій

11.1.1. Синус

Відзначмо основні властивості функції синус y sin x.

1.

Область

означення

функції

D(sin) ,

множина

значень

E(sin) [ 1;1].

2.

Синус — обмежена функція,

sin x 1.

3.

Синус — непарна функція, sin( x) sin x

для всіх x .

4.

Функція

y sin x

—

періодична

з

періодом

2 ,

sin(x 2 ) sin x

для всіх x .

5.

sin x 0 для x k, k ;

sin x 0

для x (2 k; 2 k), k ;

sin x 0

для x ( 2 k; 2 2 k), k .

6.

Функція зростає на проміжку

2 k

;

2

2

2 k

y

і спадає на проміжку

y sin x

2 k; 3

1

3

2 k , k .

O

2

2

2

2

x

2

7. Графік функції y sin x

—

1

синусоїда.

Рис. 11.1. Графік функції y sin x

11.1.2. Косинус

Відзначмо основні властивості функції косинус y cos x.

1.

Область

означення

функції

D(cos) ,

множина

значень

E(cos) [ 1;1].

2.	Косинус — обмежена функція,						cos x	1.
3.	Косинус — парна функція, cos( x) cos x								для всіх x .
4.	Функція y cos x			—		періодична			з періодом 2 ,
cos(x 2 ) cos x для всіх x .
5.	cos x 0 для x		k, k ;
		2
			2 k;
cos x 0 для x					2 k , k ;
		2		2

	Лекція 11. Тригонометричні функції. Ч. 2					3
				3
cos x 0			2 k;
	для x				2 k , k .
				2
	2

6. Функція зростає на проміжку

2 k; 2 k

і спадає на проміжку			y cos x	y
		, k .		1	3
2 k; 2 2 k
7. Графік функції y cos x —				2	2
				O	2 x
косинусоїда.				1
			Рис. 11.2. Графік функції y cos x

11.1.3. Тангенс

Відзначмо основні властивості функції тангенс y tg x.

1. Область означення функції D(tg) — множина всіх дійсних чи-

сел, окрім чисел x

k, k .

2

Множина значень E(tg) .

2. Тангенс — непарна функція, tg( x) tg x для всіх x D(tg).

3. Функція y tg x

— періодична з періодом

,

tg(x ) tg x

для всіх x D(tg).

4. tg x 0 для x

k, k ;

tg x 0

для x

k;

;

k , k

2

tg x 0

для x

k; k , k .

2

5. Функція зростає на промі-

y

y tg x

жку

k;

k

.

, k

2

2

O

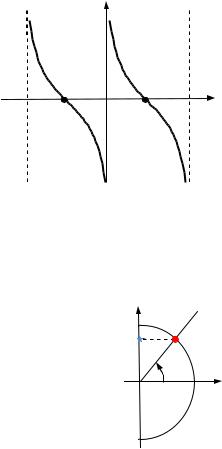
6. Графік функції y tg x

—

3 x

2

2

2

тангенсоїда.

Рис. 11.3. Графік функції y tg x

4	Лекція 11. Тригонометричні функції. Ч. 2

11.1.4. Котангенс

Відзначмо основні властивості функції котангенс y ctg x.

1. Область означення функції D(ctg) — множина всіх дійсних чисел, окрім чисел x k, k .

Множина значень E(ctg) .

2. Котангенс —			непарна				функція, ctg( x) ctg x для всіх
x D(ctg).
3. Функція y ctg x				— періодична з найменшим додатним періо-
дом , ctg(x ) ctg x для всіх x D(ctg).
4. ctg x 0 для x					k, k ;
				2
ctg x 0	для x		k;
						k , k ;
					2
ctg x 0	для x
				k; k , k .
		2

5. Функція y ctg x	спадає		y
на проміжку				y ctg x
( k; k), k .
6. Графік функції y ctg x —					x
котангенсоїда.			O
		2		2

Рис. 11.4. Графік функції y ctg x

11.2. Обернені тригонометричні функції

11.2.1. Означення обернених тригонометричних функцій

1. Арксинус. Арксинусом числа a називають									y
число t							, синус якого дорівнює a,	і поз-	a	Marcsina
				;						t
			2		2
начають arcsin a.									O	1 x
Тобто,		з	рівності arcsina t випливає, що
sin t a.

Рис. 11.5. Означення арксинуса

Лекція 11. Тригонометричні функції. Ч. 2

5

2. Арккосинус. Арккосинусом числа a називають число t 0; , косинус якого дорівнює a і

y

Marccosa

позначають arccosa.							t
Тобто,				з рівності	arccosa t випливає,	що	O	a 1 x
cost a.							Рис. 11.6. Означення
							арккосинуса
3.		Арктангенс.			Арктангенсом числа	a	називають	число
		;
t				, тангенс якого дорівнює a, і позначають arctga.
	2 2

Тобто, з рівності arctg a t випливає, що tg t a.

4. Арккотангенс. Арккотангенсом числа a	називають число
t 0; , котангенс якого дорівнює a, і позначають arcctga.
Тобто, з рівності arcctg a t випливає, що ctg t	a.

11.2.2. Формули значень тригонометричних функцій від обернених тригонометричних функцій

Формули значень тригонометричних функцій від обернених тригонометричних функцій можна звести до такої таблиці.

Їх також можна знаходити за допомогою прямокутного трикутника.

arcsin x

arccos x

arctg x

arcctg x

x

1

sin

x

1 x2

1 x2

1 x2

1

x

cos

1 x2

x

1 x2

1 x2

x

1

tg

1 x2

x

1 x2

x

x

x

1

ctg

1 x2

x

x

1 x2

x

1

x

1

1 x 2

1 x 2

1 x2

x

1

1 x2

x

1

x

3

Приміром, щоб знайти sin arctg

можна скористатись формулою

4

	sin(arctg x)		x
			1 x2

6	Лекція 11. Тригонометричні функції. Ч. 2

3

або побудувати прямокутний трикутник з гострим кутом arctg 4 ,

тобто з прилеглим до цього кута катетом 1 і протилежним катетом за-

3

вдовжки 4 (або 4 і 3 відповідно).

Далі	використовують								тео-
рему Піфагора й означення си-
нуса гострого кута:										3
		3			3		3
					4
sin arctg								.	1	4
					5		5
		4
					4

11.2. Основні характеристики обернених тригонометричних функцій

11.3.1. Арксинус

1. Функція y sin x

на відрізку

зростає і набуває всі значен-

;

2

2

ня з відрізку [ 1;1]. Тому функція y sin x

на відрізку

оборотна,

;

2

2

тобто має обернену функцію, яку називають арксинусом і позначають

yarcsin x.

2.Область означення арксинуса D(arcsin) [ 1;1], множина зна-

чень E(arcsin)
				;
			2		2	.

3.Арксинус — обмежена функція, arcsin x

4.Арксинус — непарна функція, arcsin( x) arcsin x для всіх x [ 1;1].

5.arcsin x 0 для x 0;

arcsin x 0 для x (0;1]; arcsin x 0 для x [ 1; 0).

6. Функція y arcsin x зростає на від-

різку [ 1;1].

2 .

y		y arcsin x
	2

1 O

1 x

Рис. 11.7. Графік функції y arcsin x

Лекція 11. Тригонометричні функції. Ч. 2

7

11.3.2. Арккосинус

1. Функція y cos x на відрізку 0; спадає і набуває всі значення з відрізку [ 1;1]. Тому функція y cos x на відрізку 0; має обер-

нену функцію, яку називають арккосинусом і позначають

yarccos x.

2.Область означення арккосинуса D(arccos) [ 1;1], множина

значень E(arccos)				0; .
3.		Арккосинус — обмежена функція,
	arccos x		.
	4.		arccos( x) arccos x для всіх

x [ 1;1].

y

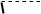
y arccos x

2

	5.	arccos x 0 для x 1;
	arccos x 0 для x [ 1;1).							1 O	1	x
	6.	Функція y arccos x спадає на від-
								Рис. 11.8. Графік функції
	різку [ 1;1].							y arccos x
	11.3.3. Арктангенс
	1.	Функція y tg x				;
			в інтервалі					зростає і набуває всіх дій-
					2		2

сних значень. Тому функція y tg x				;
	в інтервалі				має обернену
			2
					2

функцію, яку називають арктангенсом і позначають y arctg x.

2. Область означення арксинуса D(arctg) , множина значень

			;
E(arctg)				.
		2
				2

3. Арктангенс — обмежена функція,		arctg x			.
					2
4. Арктангенс — непарна функ-
					y

ція, arctg( x) arctg x для всіх		y arctg x
x [ 1;1].
	2

5. arctg x 0 для x 0; arctg x 0 для x (0; ); arctg x 0 для x ( ; 0).

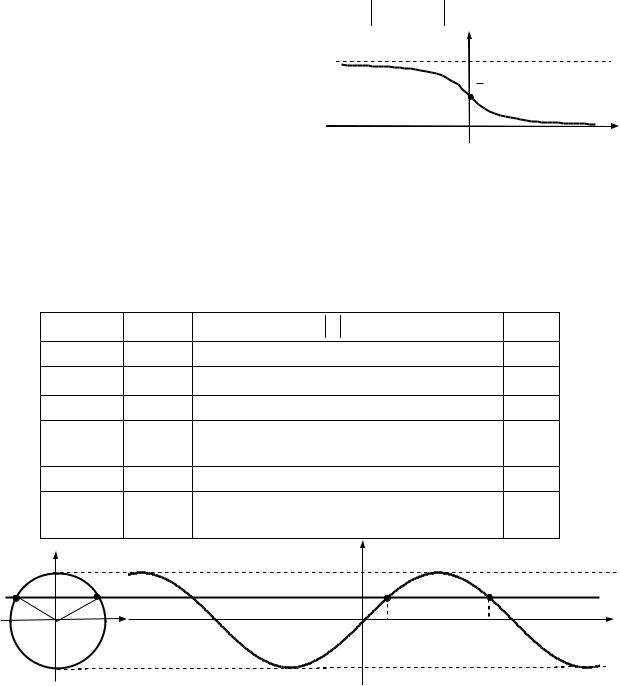
6. Функція y arctg x зростає на

.

O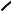

x

2

Рис. 11.9. Графік функції y arctg x

8	Лекція 11. Тригонометричні функції. Ч. 2

11.3.4. Арккотангенс

1. Функція y ctg x в інтервалі 0; спадає і набуває всіх дійс-

них значень. Тому функція y ctg x на відрізку 0; має обернену функцію, яку називають арктангенсом і позначають

yarcctg x.

2.Область означення арккотангенса D(arcctg) , множина зна-

чень E(arcctg) (0; ).

3. Арккотангенс — обмежена функція, 4. arcctg( x) arcctg x для

всіх x .

5. arcctg x 0 для x .

6. Функція y arcctg x спадає на .

arcctg x .

y		y arcctg x
	2
O		x

Рис. 11.10. Графік функції y arcctg x

11.3. Основні тригонометричні рівняння й нерівності

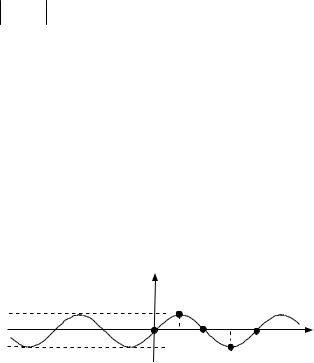
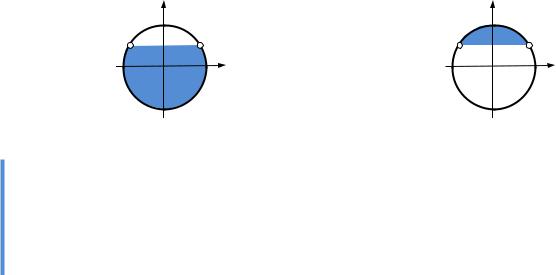
11.3.1. Основні рівняння і нерівності з синусом

		a 1	a 1	a 1
	sin x a		arcsin a 2 n x arcsin a 2 n
	sin x a		x ( 1)n arcsin a n, n
	sin x a		arcsin a 2 n x arcsin a 2 n
	sin x 1
			2 2 n, n
	sin x 0		n, n
	sin x 1
			2 2 n, n
	y		y
			1
			a	y a
		x	O			x
	1	arcsin a	arcsin a arcsin a		y	sin x
			1

		Лекція 11. Тригонометричні функції. Ч. 2						9
	sin x a				sin x a
		y				y
		a
				x		a		x
				1
	arcsin a				arcsin a

	Приклад 11.1.			Розв’язати рівняння sin x						1			і нерівності sin x
											2
	sin x 1 .
	2
	 sin x	1	x ( 1)n arcsin				1	n, n	;
		2					2
				n							2 k,
						n, n		x	6
	x ( 1)				6								k .
									5			2 k,
								x	6

	1			1		1
sin x			arcsin		2 k; arcsin
		x					2 k , k ;
	2			2		2

				7
					2 k;								;
		x								2 k , k
				6					6
	1					1						1
sin x							2 k; arcsin
		x arcsin												2 k , k ;
	2					2						2
								5
				2 k;							. 
		x							2 k , k
								6
		6

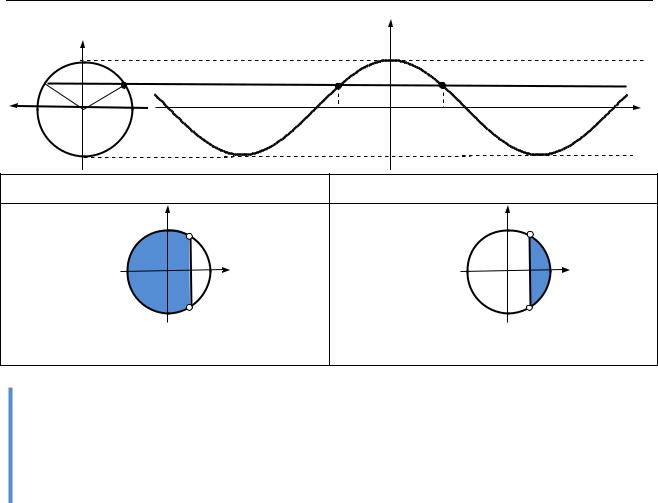
11.3.2. Основні рівняння і нерівності з косинусом

	a 1		a		1	a 1
cos x a		arccos a 2 n x 2 arccos a 2 n
cos x a		x arccosa 2 n, n
cos x a		arccos a 2 n x arccos a 2 n
cos x 1		x 2 n, n
cos x 0
		x 2 n, n
cos x 1		x 2 n, n

1 та

2

10		Лекція 11. Тригонометричні функції. Ч. 2
			y
1	x	arccosa	1
			a	y a
			O	x
y			arccosa	arccosa
				y cos x
			1
		cos x a		cos x a
		y		y
		1		a
		a x		x
		2
	arccosa			arccosa

	Приклад 11.2.				Розв’язати рівняння												cos x				1			і	нерівності cos x			1
																												2
																						2
	та cos x 1 .
	2
	 cos x	1	x arccos 1 2 n, n ;
		2								2
																			2 n,
	x						2 n, n									x		3							k .
						3
																				2 n,
																x			3
		1								1														1
	cos x		x								2 k; 2 arccos
							arccos																			2 k , k ;
		2								2														2
													5
										2 k;
							x										2 k , k .
														3
							3
			1									1									1
	cos x													2 k; arccos													;
				x arccos																				2 k , k
			2									2									2
						x				2 k;												. 
															2 k , k
								3						3