Геометрія ( 1 курс) - лекції / лекції з анал. геом. 4

106

твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, при умові перетинаються.

Доведення. Нехай точка належить поверхні. Тоді її координати задовольнятимуть як рівняння (6), так і системи (7) та (8), в яких значення параметрів - та потрібно вибрати, як розв’язки рівнянь, одержаних із систем після підставляння координат точки . Таким чином, через кожну точку поверхні проходить хоча б по одній прямій з кожної - та - параметричних сімей прямолінійних твірних.

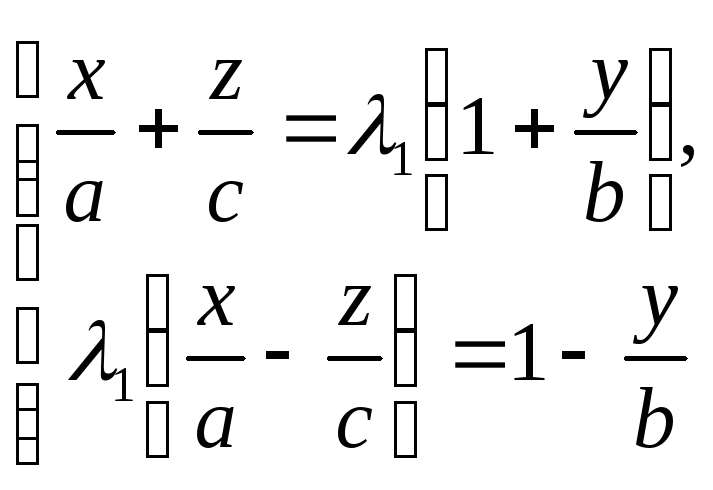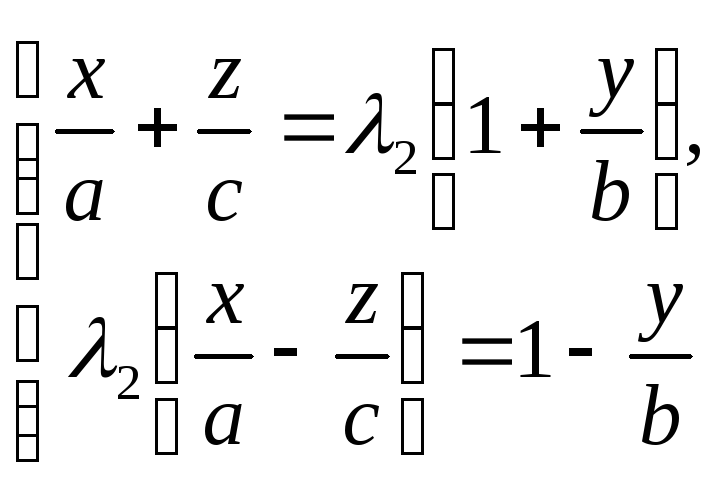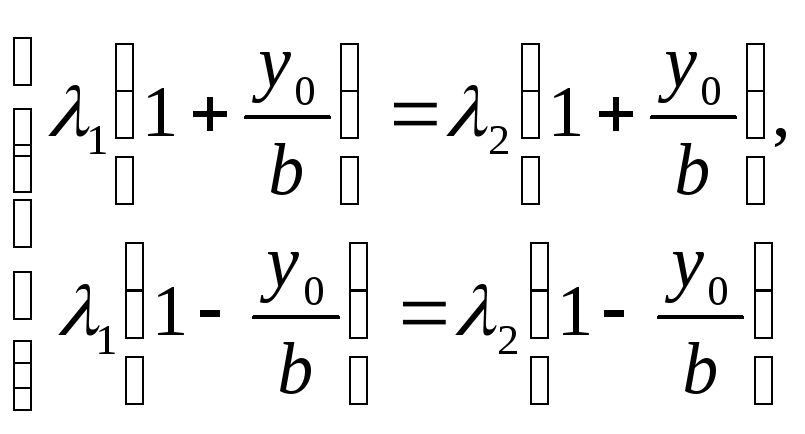Тепер припустимо, що через точку проходить дві різні прямі та , визначені системою (₇) при різних значеннях параметрів . Тоді з рівностей випливає, що , що суперечить припущенню. Цим самим показано, що дві різні прямі, визначені системою (₇) (аналогічно системою (8)), не можуть мати спільних точок.

Для того, щоб встановити, як розташовані дві прямолінійні твірні, визначені різними системами, дослідимо на сумісність систему, утворену із рівнянь систем (₇) та (₈). Використовуючи методи лінійної алгебри, знайдемо ранги основної та розширеної матриць, складених із коефіцієнтів біля змінних та вільних членів.

.

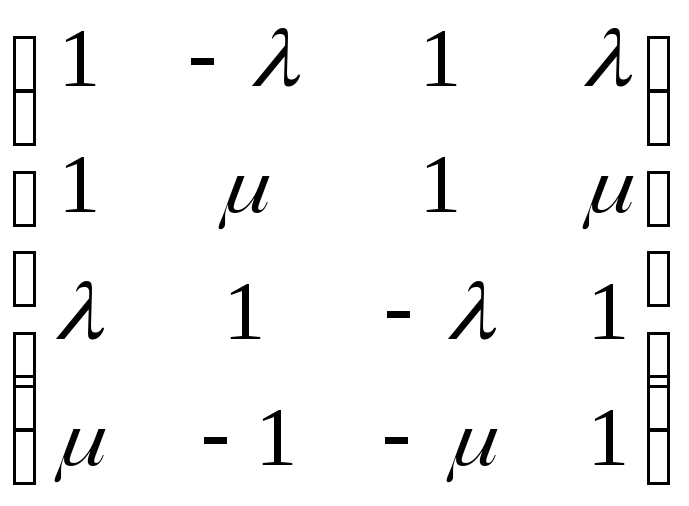
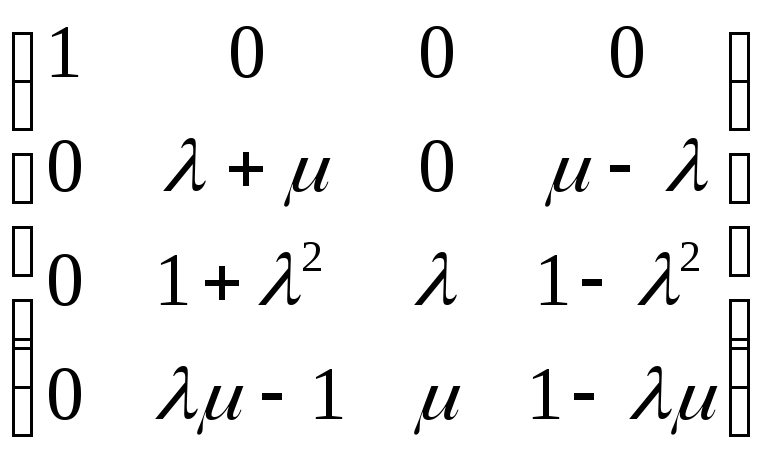Якщо тепер або , але , то легко бачити, що ранги матриць рівні, тобто система рівнянь сумісна. Якщо , то одержану матрицю можна звести до виду 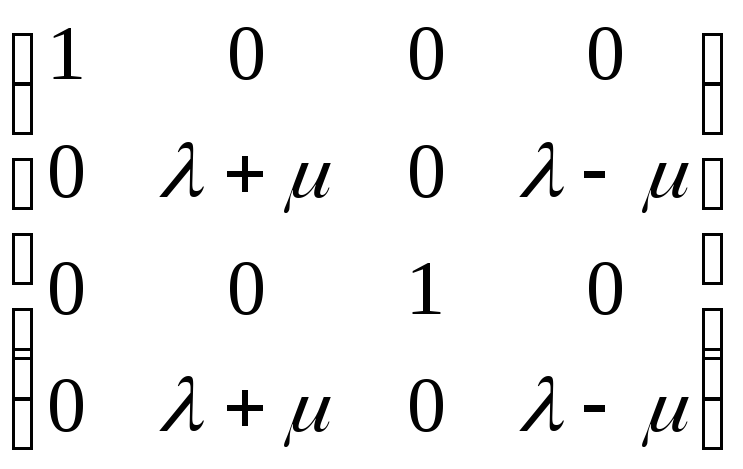, звідки видно, що якщо , то ранги матриць рівні, тобто система рівнянь сумісна, а прямолінійні твірні перетинаються. При ранги матриць різні, тому система несумісна. Теорема доведена.

Цікаво встановити, як розташовані прямі у випадку . Для цього ще раз розглянемо системи (7) та (8), поклавши у системі (8) . Знайдемо напрямні вектори та прямих (7) та (8), як векторні добутки векторів, перпендикулярних до площин, при перетині яких утворюються прямі. Маємо:

,

.

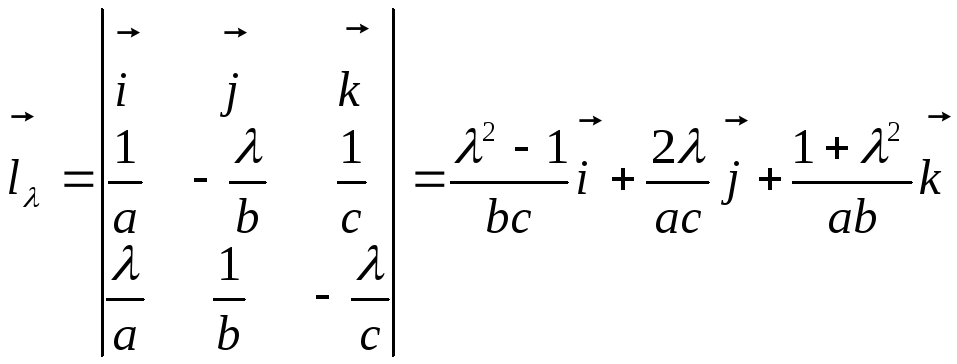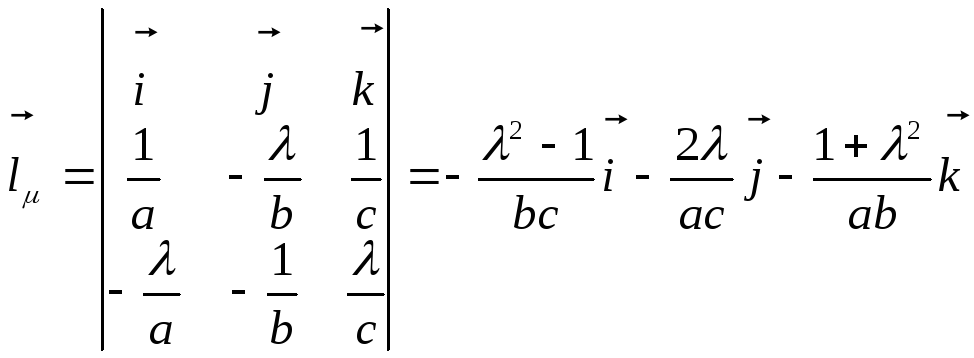Як бачимо, вектори та колінеарні, тому прямі (7) та (8) паралельні. Зауважимо, що на даний факт не звернули увагу автори [1], що привело до невірного формулювання теореми 2 у §169.

Розглянемо гіперболічний параболоїд, заданий рівнянням , яке запишемо у виді

. (9)

Розглянемо системи рівнянь

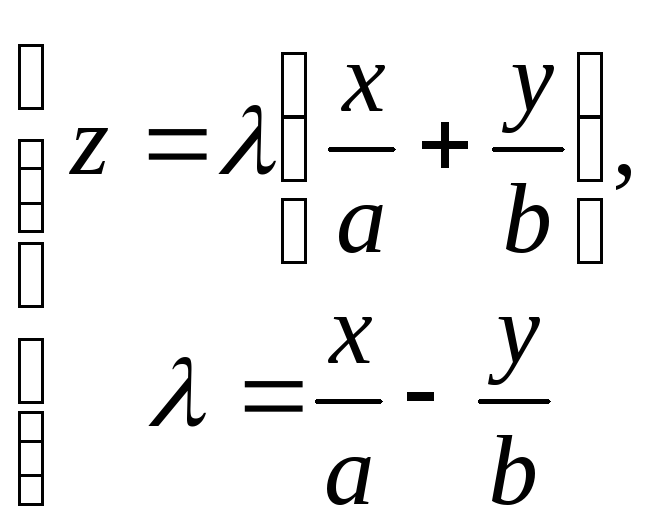(₁₀)

та

, (₁₁)

де та - довільні параметри. Як і в попередньому випадку, кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Дві довільні площини, які задаються рівняннями кожної системи, перетинаються, тому ці системи задають - та - параметричні множини прямих. Очевидно, що кожний розв’язок систем (₁₀) та (₁₁) задовольняє рівняння (9), тому вони задають - та - параметричні сім’ї прямолінійних твірних гіперболічного параболоїда.

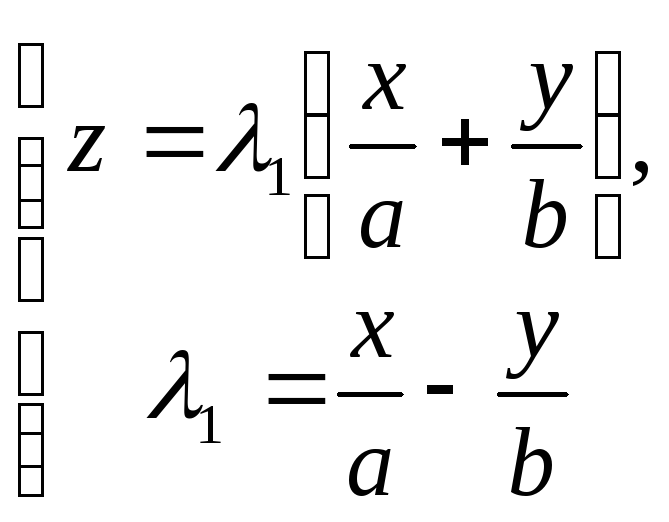Через кожну точку гіперболічного параболоїда проходить рівно по одній прямій з кожної - та - параметричних сімей прямих (₁₀) та (₁₁). Дві довільні прямолінійні твірні, які визначаються однією системою, мимобіжні, а дві прямолінійні твірні, визначені різними системами, перетинаються. Справді, припустимо, що через точку проходить дві різні прямі та 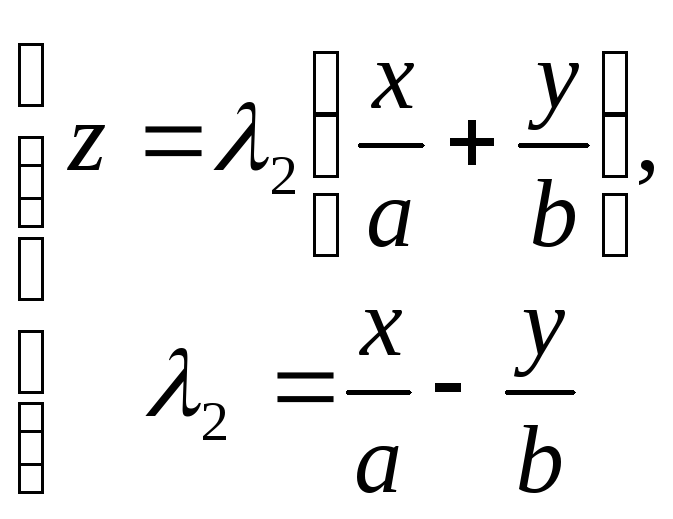, одержані із системи (₁₀) при та . Тоді з других рівнянь систем випливає, що , що вказує на помилковість припущення. Оскільки дві різні прямі, визначені системою (₁₀), не можуть мати спільних точок і не паралельні, то вони мимобіжні. Аналогічні міркування здійснюються у випадку системи (11).

У випадку двох прямолінійних твірних, визначених різними системами, висновок про їхній перетин випливає із сумісності системи

,

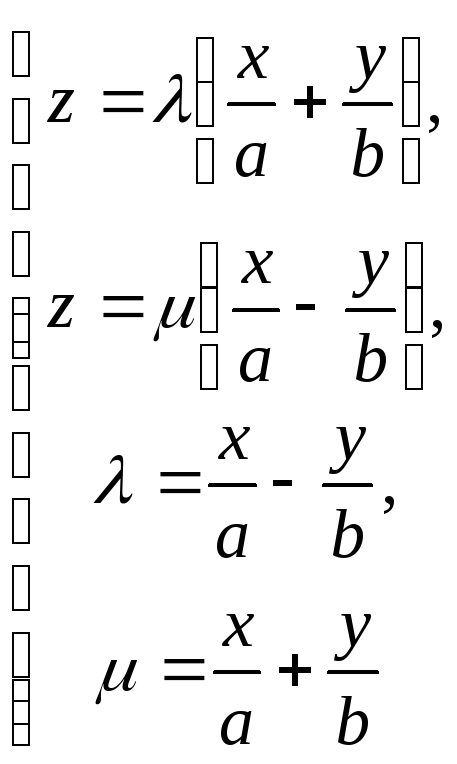розв’язком якої є .

Зауважимо, що прямолінійні твірні розглянутих вище поверхонь мають технічні застосування. Зокрема, несучі конструкції даху олімпійського зимового палацу в японському місті Саппоро, який має форму гіперболічного параболоїда, зроблені у вигляді металевих балок, які є прямолінійними твірними поверхні. Конструкції з металевих балок, які зафіксовані так, як проходять прямолінійні твірні однопорожнинного гіперболоїда обертання, використовуються при будівництві водонапірних башт, телевізійних вишок.

Розглянемо приклади розв’язання задач.

Задача 1. Скласти рівняння поверхні, утвореної обертанням прямої навколо осі .

Розв’язання. Нехай точка належить поверхні обертання. Проведемо через цю точку площину, перпендикулярно до осі . Нехай вона перетинає вісь в деякій точці та задану пряму в точці . Оскільки площина перетинає поверхню обертання по колу, то , звідки або . Очевидно, що ця поверхня являє собою однопорожнинний гіперболоїд обертання з віссю та центром у точці ().

Задача 2. Скласти рівняння поверхні, утвореної рухом прямої, яка одночасно перетинає три задані мимобіжні прямі та .

Розв’язання. Нехай точка належить шуканій поверхні, а пряма, що проходить через точку , перетинає задані прямі в точках та відповідно. Із колінеарності векторів та дістаємо рівності . Прирівнюючи координати, отримуємо систему рівнянь , , з якої потрібно виключити змінні параметри та . Послідовно знаходимо , звідки . Тепер із рівності дістаємо , або, остаточно, . Зауважимо, що отримане рівняння є рівнянням гіперболічного параболоїда. Його можна дістати із відомого нам рівняння , перейшовши до іншої системи координат, а саме до координатної системи, утвореної поворотом даної на кут навколо осі . Взаємно перпендикулярні прямолінійні твірні поверхні , які лежать в площині та задаються рівняннями , у цьому випадку займають положення нових координатних осей.

Лекція 18

Загальне рівняння лінії другого порядку.

План.

1. Поняття загального рівняння лінії другого порядку.

2. Перетин лінії з прямою. Частинні випадки.

3. Центр лінії.

4. Рівняння дотичної та нормалі.

1. Розглянемо алгебраїчну лінію другого порядку , задану рівнянням

, (1)

де - деякі дійсні числові коефіцієнти, причому коефіцієнти одночасно не дорівнюють нулю. Доданки називають групою старших членів, вираз - лінійною частиною, число - вільним членом рівняння. Розв’язки даного рівняння, тобто впорядковані пари чисел на координатній площині задають певну множину точок, які утворюють, взагалі кажучи, деяку лінію. З частинними випадками такого рівняння ми уже зустрічалися раніше. Наприклад, рівняння або задає коло з центром в точці , радіус якого 5, рівняння визначає гіперболу з дійсною піввіссю 3 та уявною піввіссю 2, а рівняння задає єдину точку , що стає очевидним, якщо це рівняння записати у виді .

Рівняння (1) називають загальним рівнянням лінії другого порядку, оскільки з нього можна отримати будь-яке конкретне рівняння другого порядку. Зокрема в останньому прикладі . Виділення в деяких коефіцієнтах загального рівняння множника 2 зроблено для зручності та стане зрозумілим дещо пізніше.

Оскільки рівняння (1) містить 6 коефіцієнтів, які визначаються з точністю до сталого множника, то лінія другого порядку задається, взагалі кажучи, 5 точками. В деяких випадках кількість умов, які визначають лінію другого порядку може бути меншою. Наприклад, коло задається трьома точками, взятими на ньому, парабола, як виявиться дальше, - чотирма.

З метою компактності записів у наступних викладках введемо в розгляд символи , означивши їх рівностями

,

а також

.

Вони не складні для запам’ятання. Зокрема можна трактувати, як половину похідної від функції по змінній , вважаючи при цьому змінну сталою, а - як половину похідної від функції по змінній при умові, що не змінюється.

Найближчими нашими задачами буде дослідження властивостей ліній, заданих рівнянням (1), вивчення особливостей їх розташування відносно системи координат, а також дослідження питання, скільки та які різні види ліній може визначати рівняння (1).

2. Перетнемо лінію другого порядку прямою , яка проходить через деяку точку та паралельна до вектора . Параметричні рівняння прямої запишуться у виді

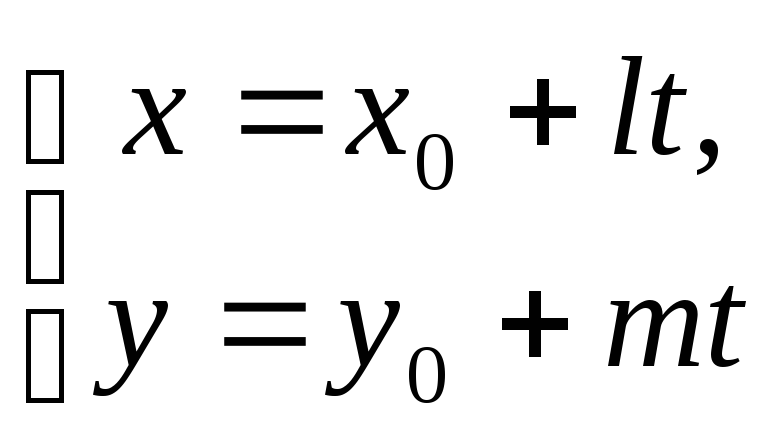. (2)

Для відшукання точок перетину лінії та прямої , дістаємо систему рівнянь

.

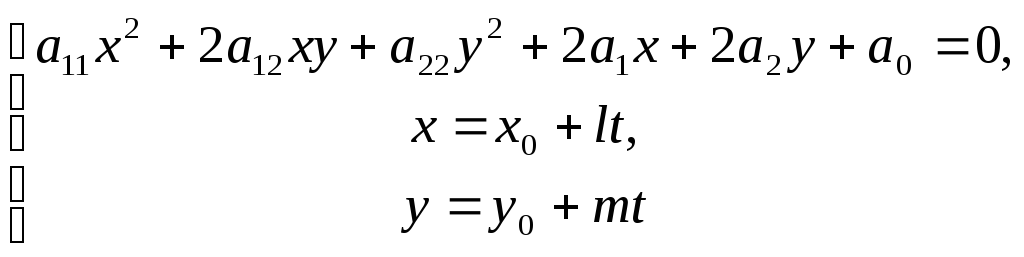Розв’язуючи її, приходимо до квадратного рівняння

, (3)

де

,

,

.

Дослідимо особливості взаємного розташування лінії та прямої у випадках, коли деякі коефіцієнти рівняння (3) рівні нулю.

1. Нехай . Оскільки один із коренів рівняння рівний 0, а йому відповідає точка , то у цьому випадку одна із точок перетину лінії та прямої співпадає з точкою (рис.1).

2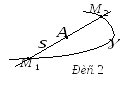. Нехай і рівняння має два дійсні корені . Даним кореням відповідають дві точки перетину . Легко бачити, що у цьому випадку точка є серединою хорди (рис. 2).

3. Нехай . Рівняння має єдиний корінь . Дослідимо, як змінюється другий корінь рівняння (3) при . Маємо

.

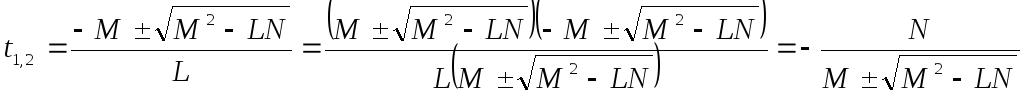О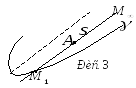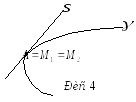чевидно, що при один із коренів рівняння прямує до , а абсолютна величина другого – до . Згідно із рівностями (2) при одна із точок перетину нескінченно віддаляється від точки . Таку точку ми будемо позначати та говорити, що пряма перетинає лінію в нескінченно віддаленій точці. Напрям прямої при цьому будемо називати асимптотичним. Асимптотичним буде, наприклад, напрям прямої, яка перетинає параболу та проведена паралельно до її осі симетрії (рис. 3).

4. Випадок є поєднанням випадків 1 та 2. Рівняння (3) матиме вид та корені . Пряма буде дотикатись до лінії у точці (рис. 4).

5. При точка належить лінії , а пряма матиме відносно асимптотичний напрям (рис. 5).

6. Якщо , то рівняння (3) не має розв’язків. У цьому випадку пряма не має з лінією спільних точок та має відносно асимптотичний напрям (рис. 6).

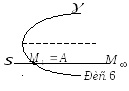
7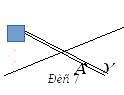. Коли , то рівняння (3) має розв’язком довільне дійсне число . Тоді кожна точка прямої належить лінії . Це можливо, наприклад, коли лінія вироджується у пару прямих (рис. 7).

3. Хордою лінії другого порядку назвемо відрізок, який сполучає дві точки на лінії.

Я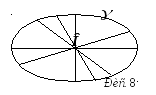кщо для лінії існує точка, в якій всі хорди, які проходять через неї, діляться пополам, то цю точку називають центром лінії. Фактично центр лінії є її центром симетрії, оскільки разом із будь-якою точкою лінії, їй належить також точка, симетрична даній відносно центра. На рисунку 8 центром лінії є точка - середина всіх можливих хорд, які проходять через неї.

Розглянемо питання відшукання центра лінії, яка задана рівнянням (1). Згідно з попереднім пунктом, умовою того, щоб точка була серединою хорд, які проходить через неї, є виконання рівності . Оскільки дана умова повинна виконуватися для довільного напрямку, заданого вектором , тобто для довільних та , то для відшукання центра лінії дістаємо систему рівнянь

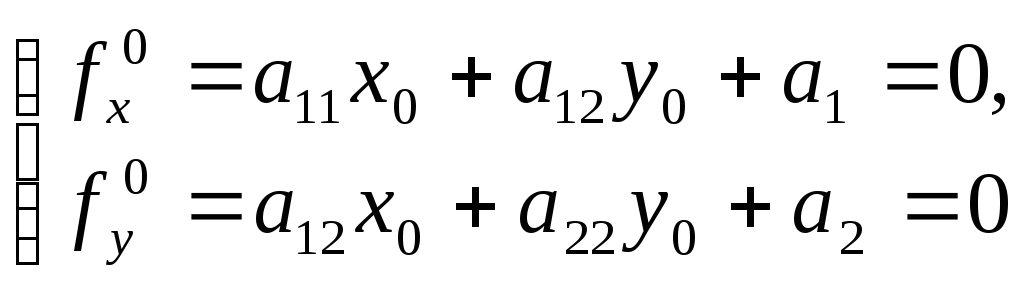. (4)

Існування та кількість розв’язків системи (4) залежить від визначника . Якщо , то система (4) має єдиний розв’язок. У цьому випадку лінія має єдиний центр і її називають центральною. Прикладами таких ліній є еліпс, гіпербола, лінія другого порядку, яка вироджується у пару прямих, які перетинаються.

Якщо , то система (4) має безліч, або не має жодного розв’язку. Лінію в цьому випадку називають нецентральною. Прикладами таких ліній є парабола, пара паралельних прямих. В останньому випадку центри лінії утворюють пряму, яка є середньою лінією смужки, утвореної даними паралельними прямими.

Приклад 1. Знайти центр лінії, заданої рівнянням .

Розв’язання. Складемо та розв’яжемо систему рівнянь 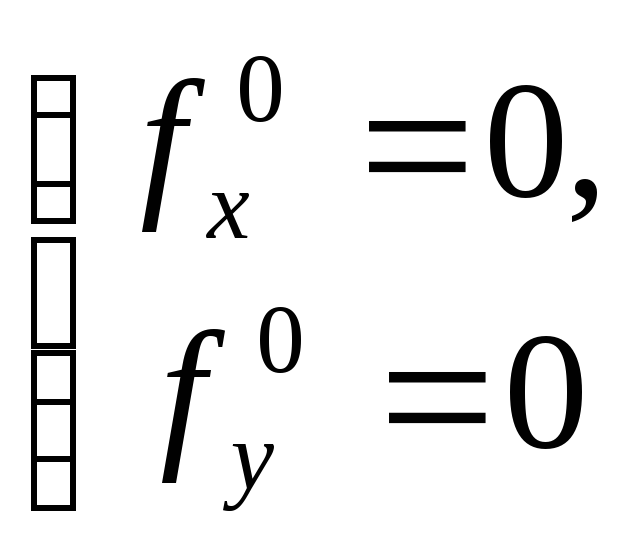. Дістаємо , звідки . Отже, задана лінія має єдиний центр, який знаходиться в точці .

4. Розглянемо питання відшукання рівняння дотичних, проведених до лінії, заданої рівнянням (1). Згідно з попереднім, пряма буде дотичною до лінії , якщо для рівняння , яке характеризує перетин прямої з лінією , виконуються умови . Нехай точка належить лінії, тобто . Умову запишемо у виді рівності . Введемо в розгляд вектор . Оскільки одержану рівність можна записати у виді , що фактично означає, що , то вектор буде перпендикулярним до шуканої дотичної. Таким чином, рівняння дотичної, проведеної до лінії в точці , запишеться у виді