Кривые второго порядка

Учреждение образования Федерации профсоюзов Беларуси «Международный университет «МИТСО»

Факультет международных экономических отношений и менеджмента

Кафедра логистики

ВЫСШАЯ МАТЕМАТИКА

Практикум для самостоятельной работы студентов

по теме «Кривые второго порядка »

Автор-составитель: О.А. Мокеева, канд. физ.-мат. наук, доцент

Минск 2011

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература Учебники

1.Высшая математика: Общий курс: учеб. для вузов / А.В. Кузнецов [и др.]; под ред. А.И. Яблонского. − Мн.: Выш. шк., 1993. − 349 с.

2.Карасев, А.И. Курс высшей математики для экономических вузов. Ч. 1. Основы высшей математики: учеб. пособие для студ. экон. спец. вузов / А.И. Карасев, З.М. Аксютина, Т.И. Савельева. − М.:

Высш. шк., 1982. − 272 с.

3.Кудрявцев, В.А. Краткий курс высшей математики: учеб. пособие для естеств. спец. ун-тов / В.А. Кудрявцев, Б.П. Демидович. − М.:

Наука, 1989. − 656 с.

4.Марков, Л.Н. Высшая математика. Ч. 1. Элементы линейной и векторной алгебры. Основы аналитической геометрии: учеб. пособие для вузов / Л.Н. Марков, Г.П. Размыслович. − Мн.: Амалфея, 1999. − 208 с.

5.Минюк, С.А. Высшая математика: учеб. пособие для вузов / С.А. Минюк, Е.А. Ровба. − Гродно: ГрГУ, 2000. − 394 с.

6.Шипачев, В.С. Высшая математика: учеб. для немат. спец. вузов

/В.С. Шипачев; под ред. А.Н. Тихонова. − М.: Высш. шк., 1990. − 479 с.

Задачники

7.Гусак, А.А. Задачи и упражнения по высшей математике. В 2 ч. Ч. 1: учеб. пособие для вузов / А.А. Гусак. − Мн.: Выш. шк., 1988. − 246 с.

8.Минорский, В.П. Сборник задач по высшей математике: учеб. пособие для втузов / В.П. Минорский. − М.: Наука, 1987. − 349 с.

9.Сборник задач и упражнений по высшей математике: Общий курс: учеб. пособие / А.В. Кузнецов [и др.]. − Мн.: Выш. шк., 1994. − 284 с.

10.Сборник индивидуальных заданий по высшей математике.

В3 ч. Ч. 1: учеб. пособие для вузов / А.П. Рябушко [и др.]; под ред.

А.П. Рябушко. − Мн.: Выш. шк., 1990. − 269 с.

2

Дополнительная литература Учебники

11.Высшая математика для экономистов: учеб. для вузов / Н.Ш. Кремер [и др.]; под ред. Н.Ш. Кремера. − М.: ЮНИТИ, 2002. − 471 с.

12.Гусак, А.А. Высшая математика. В 2 т. Т. 1: учеб. пособие для вузов / А.А. Гусак. − Мн.: ТетраСистемс, 1998. − 544 с.

13.Данко, П.Е. Высшая математика в упражнениях и задачах.

В2 ч. Ч. 1: учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. − М.: Оникс, 2002. − 304 с.

14.Красс, М.С. Математика для экономических специальностей: учеб. для вузов / М.С. Красс. − М.: Дело, 2002. − 704 с.

15.Шипачев, В.С. Высшая математика: учеб. для вузов / В.С. Ши-

пачев. − М.: Высш. шк., 1998. − 479 с.

16.Малыхин, В.И. Математика в экономике / В.И. Малыхин. − М.:

ИНФРА-М, 2002. − 352 с.

17.Высшая математика / А.В. Кузнецов [и др.]. − Мн.: Высшая школа, 1993.

18.Математический словарь высшей школы / В.Т. Воднев [и др.]. − Мн.: Высшая школа, 1984.

19.Кастрица, О.А. Высшая математика: учебное пособие / О.А. Кастрица. − Мн.: Новое знание, 2005.

Задачники

20.Гусак, А.А. Справочник по высшей математике: учеб. для вузов / А.А. Гусак, Г.М. Гусак, Е.А. Бричикова. − Мн.: ТетраСистемс, 2000. − 640 с.

21.Практикум по высшей математике для экономистов: учеб. пособие для вузов / под ред. Н.Ш. Кремера. − М.: ЮНИТИ-ДАНА, 2004.

−423 с.

Наглядные и методические пособия

22.Тютянова, В.А. Высшая математика: учебно-методический комплекс (1 курс) / В.А. Тютянова. − Гомель: ГФ МИТСО, 2007. − 145 с.

23.Электронный учебно-методический комплекс «Высшая математика» / Ю.И. Воротницкий [и др.]. − Мн.: БГУ, 2009. −

3

КРИВЫЕ ВТОРОГО ПОРЯДКА

Кривыми второго порядка называются линии, определяемые в декартовых координатах алгебраическими уравнениями второй степени относительно переменных x и y :

Ax2 2Bxy	Cy 2 2Dx 2Ey F 0 ( A2 B2 C2 0 ),
где A, B, C, D, E,	F − постоянные действительные числа.

В частности, окружность, эллипс, гипербола и парабола являются такими линиями.

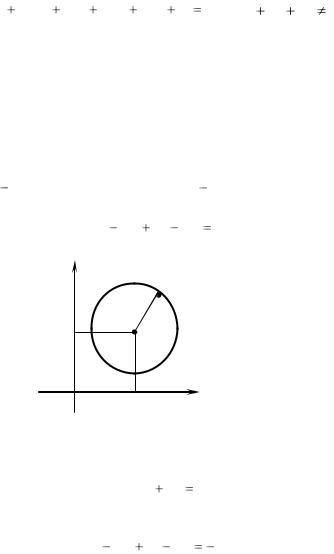
1. Окружность

Окружностью называется множество всех точек плоскости, равноудаленных от заданной точки, называемой центром (рис.1). Радиусом окружности называют расстояние от ее точек до центра.

Если R радиус окружности, а C(a;b) ее центр, то уравнение ок-

ружности имеет вид:

(x a)2 ( y b)2 R2 .

y

R

b

0 a x

Рис. 1

В частности, если центр окружности совпадает с началом коорди-

нат, то уравнение окружности:	x2	y2	R2 .
Замечания.
1) уравнение вида (x a)2	( y	b)2	R2 является уравнением

мнимой окружности. Данное уравнение не определяет никакой ли-

нии, так как правая часть уравнения отрицательна, а левая часть не может быть числом отрицательным;

2) уравнению вида (x a)2 ( y b)2 0 удовлетворяет единственная точка плоскости C(a;b) . Но, впрочем, можно говорить, что дан-

ное уравнение и в этом случае является уравнением окружности, но окружности, выродившейся в точку (окружности с нулевым радиусом).

Пример 1.1. Доказать, что уравнение x2 y2 4x 6 y 12 0 яв-

ляется уравнением окружности. Найти ее центр и радиус.

Решение. Преобразуем левую часть данного уравнения, выделив полные квадраты относительно x и y . Дополним выражения x2 4x

и y2 6 y до полных квадратов,	прибавляя и вычитая к первому дву-
члену 4, а ко второму 9:
(x2 4x 4) 4 ( y2		6 y 9) 9 12 0 ,
(x 2)2 ( y 3)2		4 9 12 0 ,
(x 2)2	( y 3)2		25 0 ,
(x 2)2	( y 3)2		52 .

Это уравнение представляет собой уравнение окружности с цен-

тром C(2;	3) и радиусом, равным 5.
Ответ:	C(2; 3) , R	5 .
Пример	1.2. Найти	координаты центра и радиус	окружности
2x2 2 y2	8x 7 y 5 0 .
Решение. В данном уравнении коэффициенты при x2			и y 2 не рав-

ны единице. Разделив уравнение на 2 и сгруппировав члены уравне-

ния,	получим: x2			4x y2		7	y		5			0 .	Дополним					выражения
					2				2
x2	4x и y2	7	y до полных квадратов:
	2
	x 2 2 2x 22			22	y 2			2		7		y	7	2	7		2		5	0 ,
									4				4		4			2

5

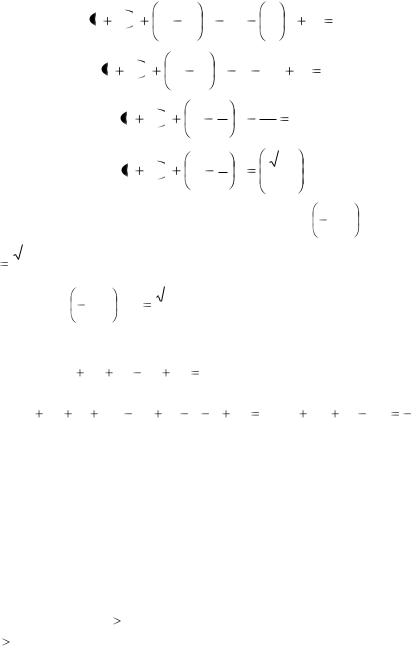
x 2 2	y	7		2				22	7			2			5	0 ,
		4							4						2
x 2 2		y			7		2	4	49 5							0 ,
					4				16				2

x2

x2

2

2

y7

4

y7

4

273 0 ,

16

	2				2
		73
					.
		4

	Таким образом,							центр окружности в точке C						2;		7	, а радиус
															4
R		73			.
	4
							7
	Ответ: C					2;		,	R	73			.
						4				4
	Пример 1.3. Установить, какую линию определяет следующее
уравнение: x2						y2		6x 6 y 22 0 .
	Решение. Преобразуем уравнение:
		(x2 6x 9) ( y2							6 y 9) 9 9 22 0 , (x 3)2						( y 3)2			4.

Данное уравнение не определяет никакой линии и является уравнением мнимой окружности.

Ответ: Ø.

2. Эллипс

Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами (рис. 2).

Постоянную величину, входящую в определение эллипса, обозна-

чают через 2a (a 0) , а расстояние между фокусами через 2c

(c 0) .

6

Каноническое уравнение эллипса:

x2

y

2

1,

(1)

a2

b2

где a большая полуось, b

малая полуось эллипса, a

b .

y

B2

M x; y

r1

r2

A

O

A2

x

1

F1

c;0

F2 c;0

x

a

x

a

B1

Рис. 2

Фокусы эллипса расположены в точках

F1( c;0) ,

F2 (c;0) , где c

половина расстояния между фокусами.

Точки A1( a;0) , A2 (a;0) , B1(0;

b) , B2 (0;b) называются вершина-

ми эллипса, точка O (0,0)

центром эллипса. Расстояние между вер-

шинами A1 и A2 , равное 2a , называется большой осью эллипса, а расстояние между вершинами B1 и B2 , равное 2b , − его малой осью.

Числа a , b и c связаны соотношением c2 a2 b2 .

Форма эллипса (мера его «сжатия» к оси Ox ) характеризуется его

	эксцентриситетом. Эксцентриситетом	(«эпсилон») эллипса назы-
	вается отношение фокусного расстояния	2c к большой оси	2a :	c
				a

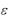( 1 , т. к. c a ).

Чем больше эксцентриситет, тем более сплющен эллипс; чем ближе эксцентриситет к нулю, тем больше форма эллипса приближается к окружности. При 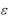0 эллипс является окружностью.

Расстояния r1 и r2 от произвольной точки M (x ; y) эллипса до его

фокусов называются фокальными радиусами этой точки. Фокальные радиусы определяются формулами:

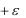
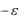
r1 a x , r2 a x , r1 r2 2a .

7

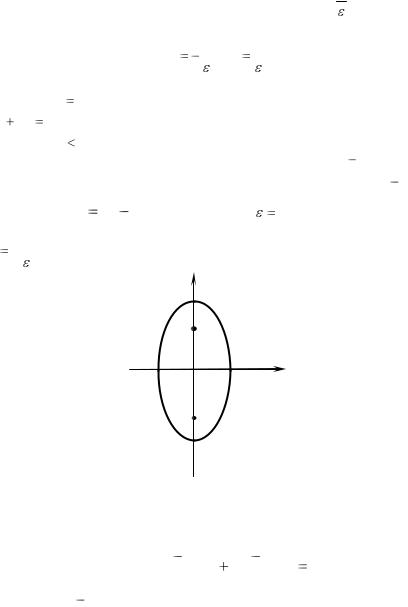
Директрисами эллипса называются прямые параллельные малой оси эллипса и отстоящие от нее на расстоянии, равном a .

Уравнения директрис:

x

a

и x

a

.

Замечания.

1) если a

b , то уравнение (1) определяет окружность

x2

y2

a2 ;

2) если a

b , то уравнение (1) определяет эллипс, большая ось ко-

торого

2b

расположена

на оси Oy , а

малая

ось 2a

на оси

Ox

(рис.3). Фокусы такого

эллипса находятся в

точках

F1(0; c)

и

F (0;c) , где c2 b2 a2

. В этом случае:

c

, уравнения директрис

2

b

y

b

;

y

B2

F2

A1

O

A2

x

F1

B1

Рис. 3

3) уравнение эллипса с осями, параллельными координатным, имеет вид:

(x x )2		( y y	0	)2
0					1,	(2)
a2		b2

где (x0; y0 ) координаты центра эллипса.

8

Пример 2.1. Показать, что уравнение 4x2 y2 8x 2 y 11 0 оп-

ределяет эллипс, найти его полуоси, координаты центра и эксцентриситет.

Решение. Преобразуем данное уравнение кривой. Так как

4x2	y2	8x 2 y 11 4 (x2				2x) ( y2			2 y) 11 4 (x2						2x 1 1)
( y2	2 y	1	1)	11	4 ((x	1)2	1)	(( y		1)2		1)	11 4		(x	1)2 4
( y	1)2	1	11	4 (x	1)2	( y	1)2	16,
то уравнение можно переписать в виде:									4 (x			1)2	( y		1)2	16 . Раз-
делив обе части уравнения на 16 получаем:											(x	1)2		( y	1)2	1.
												4	16

Данное уравнение вида (2). Его центр симметрии имеет координа-

ты (1; 1) . Из уравнения a2																	4 , a			2 , b2			16 , b	4 . Так как b a ,
				b2				a2
то c													16		4		12			2 3 . Эксцентриситет эллипса
	c		2 3					3				.
	b		4					2
Ответ: a								2 , b					4 ,		(1;		1) − центр эллипса,							3			.
																								2
Пример 2.2. Дано уравнение эллипса 9x2																							25 y2	225 . Найти:

1)длины его полуосей;

2)координаты фокусов;

3)эксцентриситет эллипса;

4)уравнения директрис и расстояние между ними.

Решение. Приведем уравнение эллипса к виду (1). Для этого разде-

лим обе его части на 225. Получим

x2

y2

1.

25

9

1)

Из канонического уравнения эллипса:

a2

25, a

5

и b2 9 ,

b 3 .

2)

Так

как a

b ,

то

из соотношения

c2

a2

b2 ,

находим

c

25 9

4 .

Следовательно,

F1(

4;0)

и F2 (4;0) .

9

3)	c		4		0,8 .
	a		5
4) Уравнения директрис:													x					a			5					25		и	x	a		25	. Рас-
																						4				4						4
																				5
стояние между ними d										25				25						50					12,5 .
										4						4				4
Ответ: 1)			a		5 , b				3 ; 2) F1(							4;0) ,				F2 (4;0) ; 3)									0,8;
	4)		x			25		,	x		25		,	d		12,5 .
					4					4

3. Гипербола

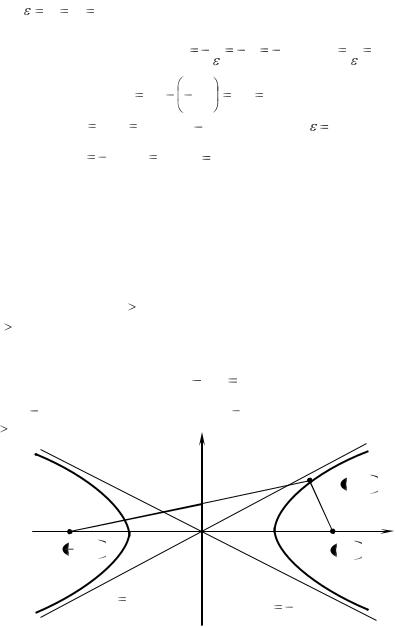
Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами (рис. 4).

Постоянную величину, входящую в определение гиперболы, обо-

значают через

2a (a

0) , а расстояние между фокусами через 2c

(c

0) .

Каноническое уравнение гиперболы:

x2

y2

1

,

(3)

a2

b2

где

a действительная полуось, b мнимая

полуось

гиперболы,

a

b .

y

b

r1

M x ; y

r2

F1

c;0

O

a

F2 c;0

x

y

a

x

a

y

x

b

b

Рис. 4

10