6 Статистические модели в виде нелинейных полиномов

При составлении статистических моделей объектов химической техно­логии нередко возникает необходимость использовать нелинейную форму связи, чаще - параболу второй, третьей или более высоких степеней, ре­же - логарифмическую, гиперболическую, степенную иди показательную функциональные зависимости. В таких случаях применяют метод регресси­онного анализа, который с учетом особенностей конкретных объектов при­обретает ту или иную разновидность. Чаще всего использую так называе­мый метод классического регрессионного анализа для составления статис­тической модели в виде полинома второй (или более высокой) степени, т.е. уравнение типа (а).

Определение коэффициентов в уравнении(а), например, для полинома второй степени при т переменных, производят приемами, аналогичными рассмотренным ранее. Однако в этом случае не требуется находить выбо­рочные коэффициенты корреляции, которые при нелинейной форме зависи­мости между исследуемыми переменными теряют смысл. Итак, если степень полинома выбрана заранее, то коэффициенты регрессии определяются по методы наименьших квадратов, а исследование уравнения проводится по статистическим критериям (в частности, адекватность модели устанавли­вается по критериям Фишера, как и в случае линейной регрессии).

Метод классического регрессионного анализа достаточно успешно применяется при составлении математических моделей химико-технологи­ческих, металлургических и других процессов.

Метод Брандона

Если на основании предварительных исследований примерно известен качественный характер влияния каждого фактора х_i на выходной параметр y (линейная или нелинейная зависимость), то можно применять метод Брандона. Метод предполагает, что аппроксимирующая функция имеет вид:

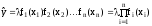(40)

где 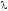- константа. для удобства проверки расчетов принимается равной

среднему экспериментальных значений входного параметра

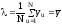(41)

Чтобы увеличить точность обработки результатов наблюдений, функции f_i (x_i) в выражении (41) следует располагать в порядке убывания влияния факторов х_i нa y. расчеты начинают с того, что нормализуют экспериментальные данные y_u, разделив их на :

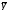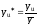u=1, 2, . . . , N. (42)

Дальнейшие операции по расчеты составляющих функций f_i(x_i) выпол­няют в следующем порядке.

1. На график наносят нормализованные значения y_u* в зависимости от значения х_1u.

2. Анализ графика с учетом априорных сведений о свойствах иссле­дуемого объекта дает возможность выбрать вид первой составляющей функ­ции (40) - f₁(x₁). В простейшем случае используют линейную функции (уравнение регрессии)

f₁(x₁) = b₀₁ + b₁₁x₁ (43)

3. Методом наименьших квадратов или любым другим методом опреде­ляют числовые значения коэффициентов параметра yu* исключают f₁(x₁) -

значения первой составляющей функции :

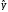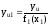(44)

5. Строят график первой остаточной функции y_u1 от значений факто­ра х₂ и определяют вид второй составляющей функции f₂ (x₂). Выбирают уравнение регрессии, которое может быть в простейшем случае линейным

f₂(x₂) = b₀₂ + b₁₂x₂ (45)

и для конкретного уравнения рассчитываю коэффициенты (например, b₀₁ и b₁₁ для уравнения (45).

6. Из значений y_u1 исключают f₂ (x₂) - значения второй составляю­щей функции (40):

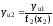(46)

7. В такой последовательности расчет повторяют до тех пор, пока не будут определены составляющие последней остаточной функции

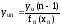(47)

которая при такой последовательности расчета должна быть близка к еди­нице.

Найденные составляющие функций f_i (x_i) включают в уравнение (40). Подстановкой экспериментальных значений x_iu (u= 1,2, ...,N; i=1,2,...,n) получают расчетные значения y_u аппроксимирующего уравне­ния (40), а затем проверяют адекватность математической модели по из­вестной уже формуле (36) с применением критерия Фишера. Если условие (36) не соблюдается, то следует повысить степень уравнений регрессии составляющих функций или ввести дополнительные факторы.

Пример 2. Предварительные исследования объекта химической техно­логии показали, что зависимость между выходом целевого продукта (выходной параметр) и каждым из 4-х факторов (давление, температура, концентрации двух иходных компонентов) (табл.14) можно представить линейными уравнениями, т.е. записать их в виде

f_i(x_i) = b_0i + b_1ix_i

Необходимо определить коэффициенты каждой составляющей функции.