Методичні вказівки
до розв`язання типових задач
Розділ 1. Алгебра
Приклад 1.1. Обчислити значення виразів:
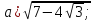
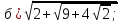

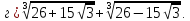
 .
.
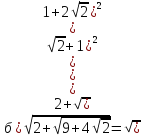
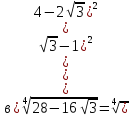
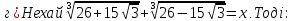
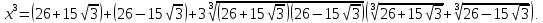

Приклад
1.2.
Знайти
корені многочлена
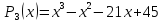 і
розкласти його на множники.
і
розкласти його на множники.
Цілі
корені многочлена
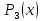 шукаємо
серед дільників вільного члена:
шукаємо
серед дільників вільного члена:
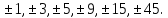 Перевіркою переконуємось, що
Перевіркою переконуємось, що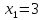 задовольняє
рівняння
задовольняє
рівняння
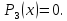 За
теоремою Безу многочлен
За
теоремою Безу многочлен
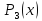 ділиться
ділиться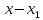 без
остачі. Виконавши ділення ( наприклад,
«кутом»), маємо:
без
остачі. Виконавши ділення ( наприклад,
«кутом»), маємо:
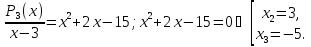
Відповідь:
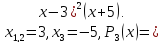
Приклад
1.3.
Розв`язати
рівняння

Оскільки
 , то маємо симетричне рівняння.
, то маємо симетричне рівняння.
Розділимо
обидві його частини на

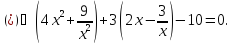
Заміна

Відповідь:
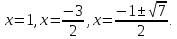
Приклад
1.4.
Розв`язати
рівняння
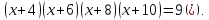
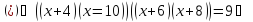
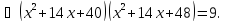
Заміна
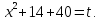
Відповідь:

Приклад
1.5.
Розв`язати
рівняння
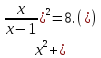
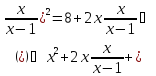
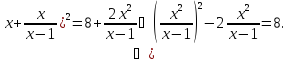 Заміна
Заміна
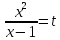 .
.
Відповідь:
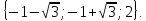
Приклад 1.6. Розв`язати рівняння

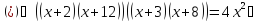

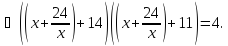
Заміна
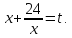
Відповідь:

Приклад
1.7.
Розв`язати
рівняння
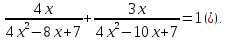
Оскільки

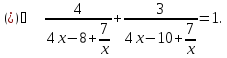
Заміна

Відповідь:
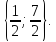
Приклад 1.8. Розв`язати рівняння:
а)
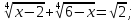 б)
б)
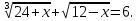
а)
Після
заміни

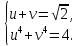
Відповідь:
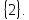
б)
Після
заміни
 одержимо
систему
одержимо
систему
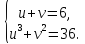
Відповідь:

Приклад
1.9.
Розв`язати
рівняння
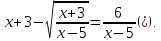
Оскільки
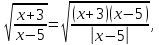
то

Відповідь:
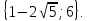
Приклад 1.10. Розв`язати рівняння:
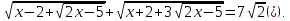
Після
заміни
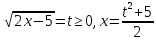 одержимо
одержимо
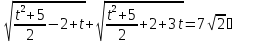
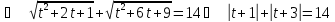
Відповідь:
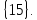
Приклад
1.11.
Розв`язати
рівняння
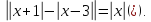
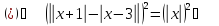
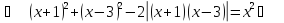
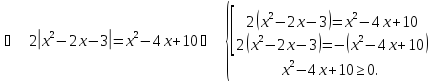
Відповідь:
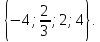
Приклад
1.12.
Для
всіх значень параметра
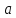 розв`язати
рівняння:
розв`язати
рівняння:
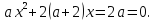
Розглянути
окремо випадки
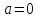 та
та
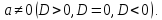
Відповідь:
якщо
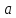
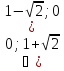 то
то

якщо
 то
то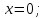
якщо
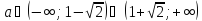 ,
то розв`язків
немає.
,
то розв`язків
немає.
Приклад
1.13.
Знайти
всі значення параметра
 при
кожному з яких корені рівняння
при
кожному з яких корені рівняння
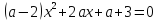 належать інтервалу
належать інтервалу
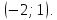
Нехай

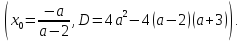
Якщо
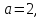 то
то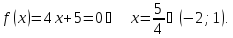
Якщо
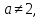 то задачарівносильна
виконанню умов:
то задачарівносильна
виконанню умов:





Відповідь:
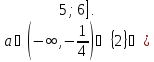
Приклад
1.14.
При
яких значеннях параметра
 корені
рівняння
корені
рівняння
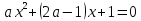 розташовані
в інтервалі
розташовані
в інтервалі
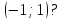
Задача зводиться до розв`язання системи нерівностей:
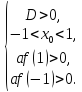
Відповідь:
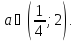
Приклад
1.15.
Розв`язати
систему рівнянь
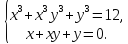 (*)
(*)
Система (*) є симетричною.
(*)
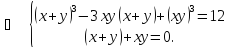
Заміна

Відповідь:
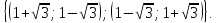
Приклад
1.16.
Розв`язати
систему рівнянь
 (*)
(*)
Система
(*) є
однорідною.
Оскільки
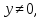 то
то
(*)

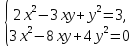

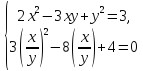

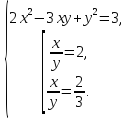
Відповідь:
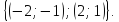
Приклад
1.17.
Розв`язати
систему рівнянь
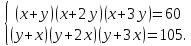 (*)
(*)
(*)

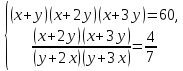


Приклад
1.18.
Розв`язати
систему рівнянь
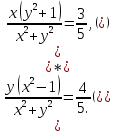
Бачимо,
що
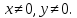 Помноживши рівняння (*) на
Помноживши рівняння (*) на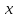 ,
а рівняння (**) на
,
а рівняння (**) на і
віднявши від першого рівняння друге,
одержимо:
і
віднявши від першого рівняння друге,
одержимо:

Розділивши
рівняння (*) на
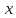 ,
а рівняння (**) на
,
а рівняння (**) на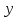 і додавши, одержимо:
і додавши, одержимо:
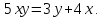
Приклад
1.19.
Розв`язати
систему рівнянь
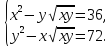 (*)
(*)
Скориставшись формулою
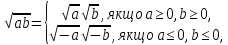
маємо:
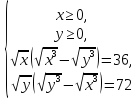 або
або

Відповідь:
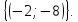
Приклад
1.20.
Розв`язати
систему рівнянь
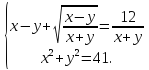 (*)
(*)
Оскільки
 то
то
(*)

 або
або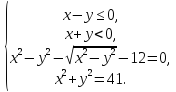
Відповідь:

Приклад
1.21.
Розв`язати
систему рівнянь
 (*)
(*)
(*)

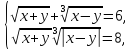

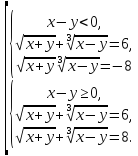
Відповідь:
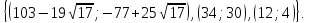
Приклад 1.22. Розв`язати нерівність
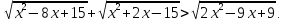 (*)
(*)
ОДЗ:
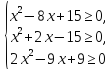




Оскільки
число
 нерівність (*) не задовольняє і обидві
частини нерівності (*) невід`ємні, то
після піднесення (двічі) до квадрату і
спрощення маємо:
нерівність (*) не задовольняє і обидві
частини нерівності (*) невід`ємні, то
після піднесення (двічі) до квадрату і
спрощення маємо:
(*)
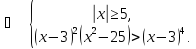
Відповідь:
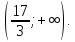
Приклад 1.23. Розв`язати нерівність

(*)
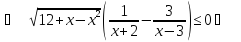
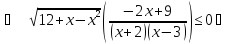

Відповідь:
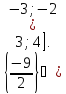
Приклад
1.24.
Розв`язати
нерівність
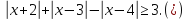
Методом інтервалів знаходимо інтервали знакосталості виразів
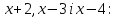

Отже:
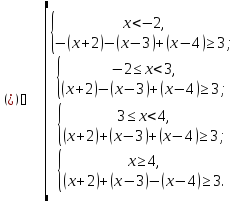
Відповідь:
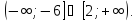
Приклад
1.25.
Розв`язати
нерівність
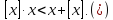
На
проміжках
 нерівність
нерівність
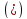
еквівалентна
сукупності системи
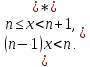
Розглянути
чотири випадки:
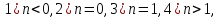 неважко
переконатись, що при
неважко
переконатись, що при
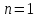 та
та
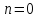 розв`язками
системи (**) будуть множини [1;2)
та (0;1) відповідно,
а при
розв`язками
системи (**) будуть множини [1;2)
та (0;1) відповідно,
а при
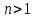 та
та
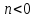 система (**)
розв`язків
не має.
система (**)
розв`язків
не має.
Відповідь: (0;2).
Приклад
1.26.
Розв`язати
нерівність


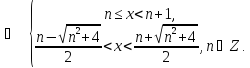
Відповідь:

Приклад
1.27.
Знайти
дійсні
значення параметра
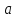 ,
при
яких нерівність
,
при
яких нерівність
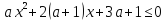
справдується
для всіх
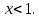
При
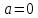 отримаємо
нерівність
отримаємо
нерівність
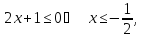
яка
не справджується для всіх

Тому
 не буде розв`язком
задачі.
не буде розв`язком
задачі.
Нехай
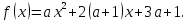
Тоді
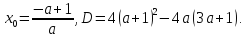
Якщо
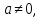 то
шукане значення параметра
то
шукане значення параметра
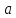 знаходимо
із сукупності систем:
знаходимо
із сукупності систем:

Відповідь:
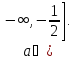
Приклад
1.28.
Для
кожного значення параметра
 розв`язати
нерівність
розв`язати
нерівність
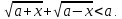
Із
(*) випливає, що
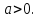 Для таких
Для таких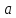 ОДЗ змінної
ОДЗ змінної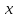 є множина
є множина Після заміни
Після заміни нерівність (*) набуде вигляду:
нерівність (*) набуде вигляду:
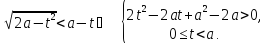
Нехай

Тоді
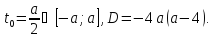
Якщо
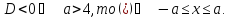
Випадок,
коли корені квадратного тричлена
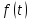 належать
множині
належать
множині
 рівносильний
виконанню умов:
рівносильний
виконанню умов:
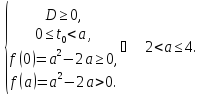
Відповідь:
якщо
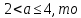
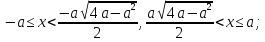
якщо
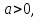 то
то
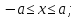
при
інших значеннях
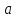 розв`язків
немає.
розв`язків
немає.
Приклад
1.29.
Для
кожного значення параметра
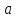 розв`язати
систему нерівностей
розв`язати
систему нерівностей

I
спосіб.
Розгляньте
взаємне розміщення коренів
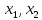 рівняння
рівняння
 та
коренів
та
коренів
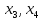 рівняння
рівняння
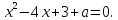
2
спосіб.
Зобразіть
на координатній площині
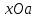 множину
точок, координати яких задовольняють
системі нерівностей
множину
точок, координати яких задовольняють
системі нерівностей
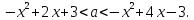
Дослідіть
перетин цієї множини сім`єю
прямих
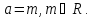
Відповідь:
якщо

якщо
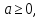 то
розв`язків
немає.
то
розв`язків
немає.
Приклад 1.30. Скільки спільних точок мають графіки функцій
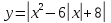 та
та
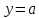 залежно
від параметра
залежно
від параметра
 ?
?
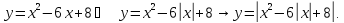

Приклад
1.31.
Скільки
спільних точок мають графіки функцій
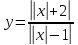 та
та
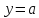
залежно
від параметра
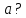
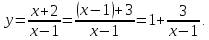
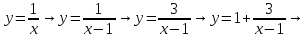
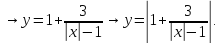

Приклад
1.32.
Скільки
спільних точок мають графіки функцій
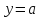 та
та
 залежно
від параметра
залежно
від параметра
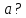
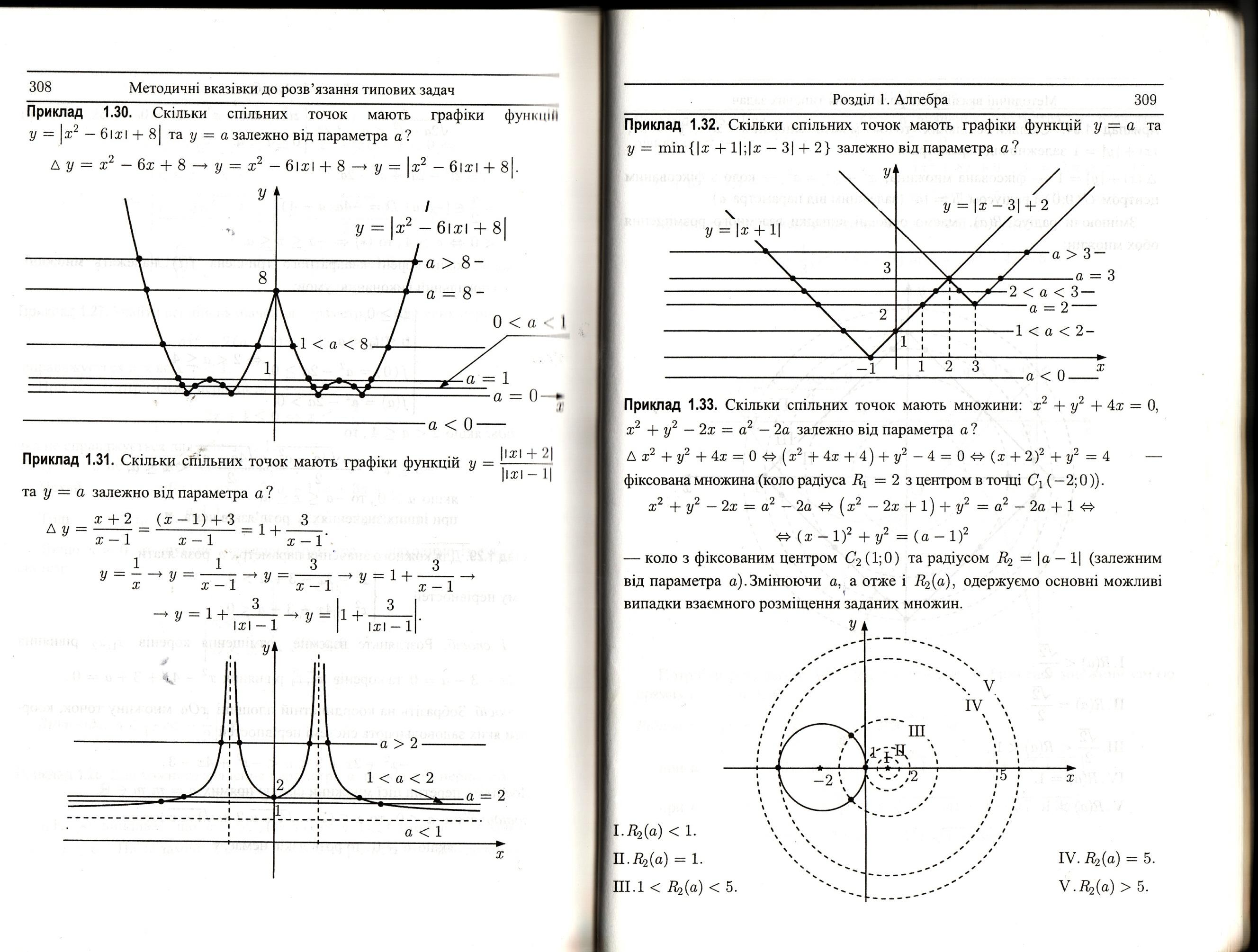
Приклад
1.33.
Скільки
спільних точок мають множини:
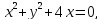
 залежно
від параметра
залежно
від параметра


фіксована
множина (коло радіуса
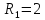 з
центром в точці
з
центром в точці
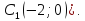
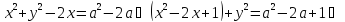

коло з фіксованим центром
 та
радіусом
та
радіусом
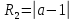 (залежним
від параметра
(залежним
від параметра
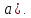 Змінюючи
Змінюючи
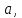 а
отже і
а
отже і
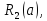 одержуємо
основні можливі випадки взаємного
розміщення заданих множин.
одержуємо
основні можливі випадки взаємного
розміщення заданих множин.
Приклад
1.34.
Скільки
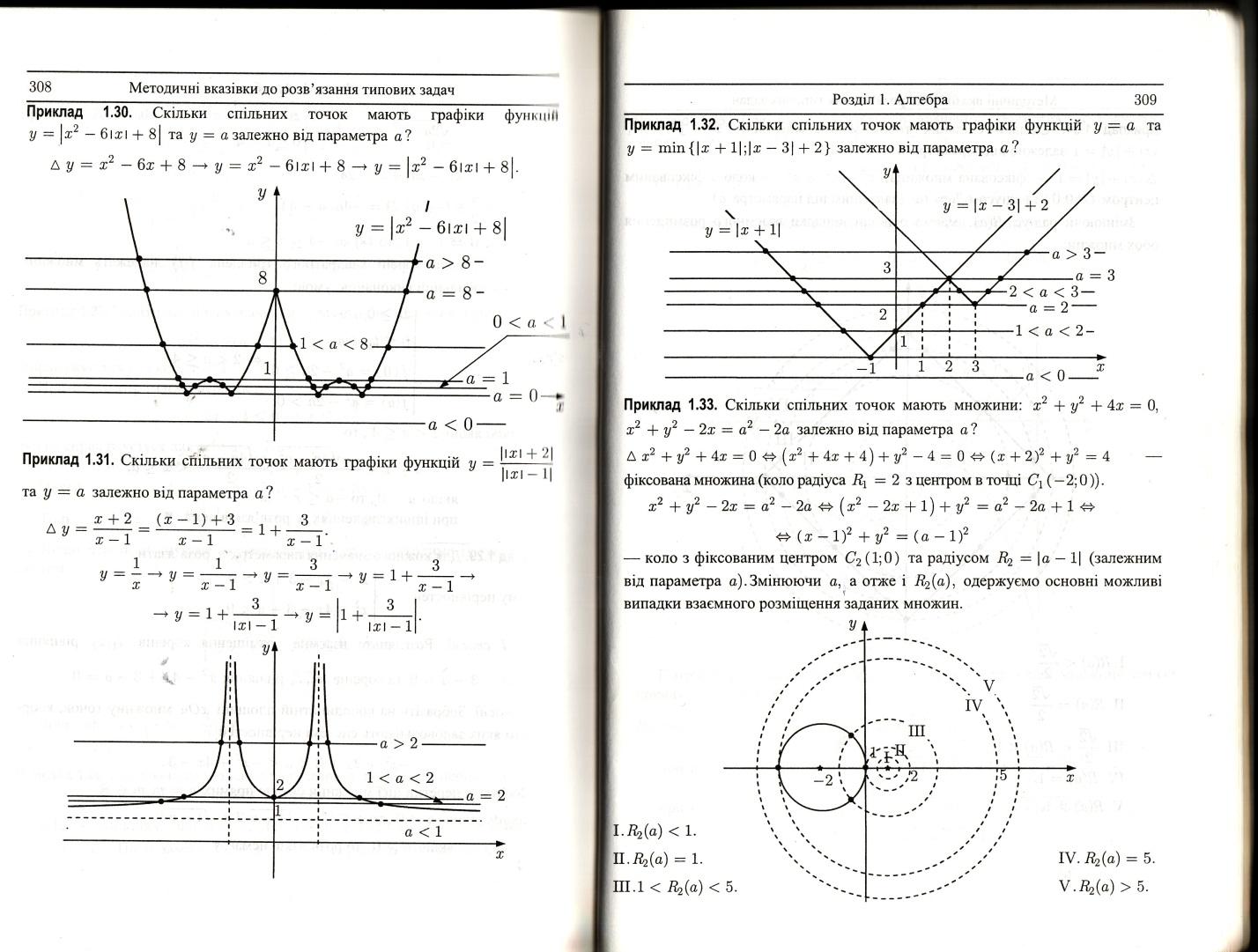
спільних точок мають множини:

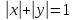 залежно
від параметра
залежно
від параметра
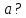
 -
фіксована множина;
-
фіксована множина;
 - коло
з фіксованим центром
- коло
з фіксованим центром
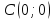 і
радіусом
і
радіусом
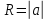 (залежним
від параметра
(залежним
від параметра
 ).
).
Змінюючи
радіус
 ,
маємо
основні випадки взаємного розміщення
обох множин:
,
маємо
основні випадки взаємного розміщення
обох множин:

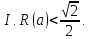
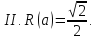
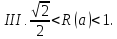
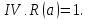
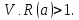
Приклад
1.35.
Для
кожного дійсного
значення параметра
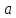 розв`язати
рівняння
розв`язати
рівняння


Можна
скористатись графіками залежностей
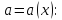
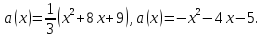

Потрібно розглянути всі варіанти перетину зображеної множини сім`єю прямих
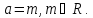
Відповідь:
при
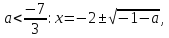
при

при
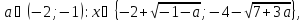
при
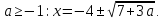
Приклад 1.36. Знайти всі значення параметра а, при кожному з яких система рівнянь
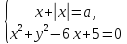
має рівно два розв’язки?
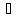 Потрібно
скористатись геометричною інтерпретацією:
розглянути взаємне розташування графіка
функції
Потрібно
скористатись геометричною інтерпретацією:
розглянути взаємне розташування графіка
функції
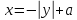 та кола
та кола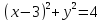 .
.

Відповідь:
a
 .
.
Приклад 1.37. Знайти всі значення параметра а, при кожному з яких система рівнянь
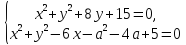
має рівно єдиний розв’язок.

Рівняння
системи є рівняннями кіл: перше коло
радіуса
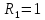 з центром у точціC1(0;-4),
друге – коло радіуса
з центром у точціC1(0;-4),
друге – коло радіуса
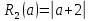 з
центром у точціC2(3;0).
з
центром у точціC2(3;0).
Система матиме єдиний розв’язок тільки за умови дотику цих кіл. Оскільки кола можуть дотикатися зовнішньо або внутрішньо, то потрібно розглянути відповідно два випадки.
Відповідь:{-8;-6;2;4}.
Приклад 1.38. Знайти всі значення параметра а, при кожному з яких система рівнянь

має рівно два розв’язки.
 Нехай
а
– шукане значення параметра і (x0;y0)
– розв’язок системи. Можна показати,
що пари чисел (-x0;-y0),(y0;x0),(-y0;-x0)
також будуть розв’язками системи.
Розв’язки (x0;y0)
і (-x0;-y0)
різні, оскільки тоді x0=0
і y0=0
та не задовольняється друге рівняння
системи. Розв’язки (x0;y0)
i
(-y0;-x0)
також різні, бо інакше
Нехай
а
– шукане значення параметра і (x0;y0)
– розв’язок системи. Можна показати,
що пари чисел (-x0;-y0),(y0;x0),(-y0;-x0)
також будуть розв’язками системи.
Розв’язки (x0;y0)
і (-x0;-y0)
різні, оскільки тоді x0=0
і y0=0
та не задовольняється друге рівняння
системи. Розв’язки (x0;y0)
i
(-y0;-x0)
також різні, бо інакше
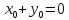 і знову не задовольняється друге рівняння
системи. За умовою система має рівно
два розв’язки, отже, розв’язки (-x0;-y0)
і (-y0;-x0)
збігаються, тобто x0=y0.
і знову не задовольняється друге рівняння
системи. За умовою система має рівно
два розв’язки, отже, розв’язки (-x0;-y0)
і (-y0;-x0)
збігаються, тобто x0=y0.
Примітка.
Можна скористатись геометричною
інтерпретацією: взаємним розміщенням
кола
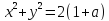 і прямих
і прямих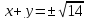 .
.
Відповідь:
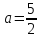 .
.
Приклад 1.39. Знайти всі значення параметра а, при кожному з яких система рівнянь

має рівно чотири розв’язки.
 Потрібно
скористатись
геометричною
інтерпретацією:
розглянути
взаємне
розміщення
фіксованої
множини
Потрібно
скористатись
геометричною
інтерпретацією:
розглянути
взаємне
розміщення
фіксованої
множини
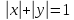 та
параметричної
сім’ї
кіл
та
параметричної
сім’ї
кіл
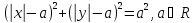 .
.
Відповідь:
 .
.
Приклад 1.40. При яких значеннях параметра а розв’язки нерівності

утворюють
проміжок довжини
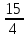 ?
Знайти цей проміжок.
?
Знайти цей проміжок.
 Скористатись
геометричною інтерпретацією: розглянути
графіки функцій
Скористатись
геометричною інтерпретацією: розглянути
графіки функцій
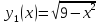 (півколо)
і
(півколо)
і .
.
Відповідь:
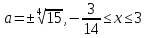 .
.
Приклад 1.41. Знайти чотири числа, з яких перші три утворюють геометричну прогресію, а останні три – арифметичну, причому сума крайніх чисел дорівнює 32, а середніх чисел – дорівнює 24.
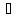 Перші
три числа складають геометричну
прогресію, позначимо їх:
Перші
три числа складають геометричну
прогресію, позначимо їх:
 ,
,
а останні три – арифметичну.
Якщо
четверте число позначити через t,
то числа
 – будуть послідовними членами арифметичної
прогресії, тоді
– будуть послідовними членами арифметичної
прогресії, тоді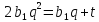 ,
звідки
,
звідки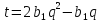 .
.
Отже, шукані числа можна записати у вигляді:
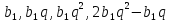 .
.
За умовами задачі:
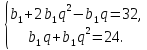 .
.
Відповідь:
32; 16; 8; 0 та 2; 6; 18; 30.
Приклад 1.42. Якщо від чотирьох чисел, які утворюють арифметичну прогресію, відняти відповідно 1,5,8 і 9, то дістнемо чотири числа, які в тому ж порядку утворюють геометричну прогресію. Знайти ці числа.
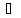 Позначимо
шукані числа через a1,a2,a3
і a4.
Тоді числа a1
– 1, a2
– 5, a3
– 8 I
a4
– 9 повинні складати геометричну
прогресію, тому:
Позначимо
шукані числа через a1,a2,a3
і a4.
Тоді числа a1
– 1, a2
– 5, a3
– 8 I
a4
– 9 повинні складати геометричну
прогресію, тому:
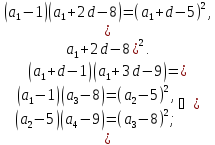
Відповідь:
2;7;12;17.
Приклад 1.43. Сума трьох чисел, які утворюють геометричну прогресію, дорівнє 65. Якщо ці числа зменшити відповідно на 1,8 і 35, то одержимо числа, які утворюють арифметичну прогресію. Знайти ці числа.
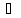 Позначимо
шукані числа через
Позначимо
шукані числа через
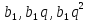 .
Тоді
.
Тоді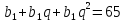 .
За умовою задачі числа
.
За умовою задачі числа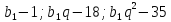 утворюють
арифметичну прогресію, тому:
утворюють
арифметичну прогресію, тому:
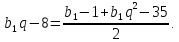
Отже, задача звожиться до розв’язування системи:
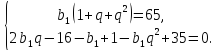
Відповідь:
5;15;45 або 45;15;5.
Приклад 1.44. Три числа, сума яких дорівнює 21, утворюють арифметичну прогресію. Якщо від другого числа відняти 1, а до третього додати 1, то одержимо числа, які утворюють геометричну прогресію. Знайти ці числа.
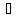 Позначимо
шукані числа
Позначимо
шукані числа
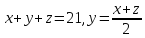 .
За умовою задачі числа
.
За умовою задачі числа утворюють
геометричну прогресію, тобто для них
виконується рівність
утворюють
геометричну прогресію, тобто для них
виконується рівність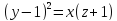 .
.
Отже, задача зводиться до розв’язання системи:
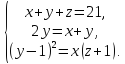
Відповідь:12;7;2
або 3;7;11.
Приклад
1.45.
Два вантажних автомобілі мають перевезти
деякий вантаж за 6 год. Другий автомобіль
затримався в гаражі, і коли він прибув
на місце завантаження, то перший
автомобіль перевіз вже
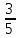 всього
вантажу. Частину вантажу, що залишилось,
перевіз другий автомобіль, і весь вантаж
був перевезений таким чином за 12 год.
За який час перевезе весь вантаж кожен
автомобіль окремо?
всього
вантажу. Частину вантажу, що залишилось,
перевіз другий автомобіль, і весь вантаж
був перевезений таким чином за 12 год.
За який час перевезе весь вантаж кожен
автомобіль окремо?
 Нехай
першому автомобілю для виконання всієї
роботи (перевезення всього вантажу)
потрібно
Нехай
першому автомобілю для виконання всієї
роботи (перевезення всього вантажу)
потрібно
 год,
а другому
год,
а другому
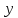 год. Узявши обсяг всієї роботи за одиницю,
згідно умови задачі, маємо систему
рівнянь:
год. Узявши обсяг всієї роботи за одиницю,
згідно умови задачі, маємо систему
рівнянь:

Відповідь:
10 год, 15 год або 12 год, 12 год.
Приклад 1.46. З посудини, яка містить 54 л чистої кислоти, відлили декілька літрів і після ього долили посудину водою до попереднього обєму. Потім з посудини відлили суміші стільки ж літрів, як за першим разом. В результаті в суміші, що містяться у посудині, залишилось 24 л чистої кислоти. Скіьки літрів кислоти вилили за першим разом?
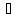 Нехай
за першим разом було відлито
Нехай
за першим разом було відлито
 л кислоти. Тоді в посудині залишилось
л кислоти. Тоді в посудині залишилось л
кислоти. Доливши посудину водою, одержимо
54 л суміші, яка містить
л
кислоти. Доливши посудину водою, одержимо
54 л суміші, яка містить
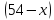 л кислоти. Отже,
в одному літрі суміші міститься
л кислоти. Отже,
в одному літрі суміші міститься
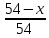 л кислоти. За другим разом з посудини
відлили
л кислоти. За другим разом з посудини
відлили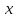 л суміші, тобто кислоти відлили
л суміші, тобто кислоти відлили л.
Отже, за першим разом було відлито
л.
Отже, за першим разом було відлито л кислоти, за другим разом
л кислоти, за другим разом л кислоти, а всього за два рази відлили
л кислоти, а всього за два рази відлили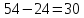 л
кислоти.
л
кислоти.
Отже,
одержуємо наступне рівняння:
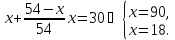
За
умовою задачі
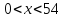 .
Отже
.
Отже .
.
Відповідь:
18л.
Приклад 1.47. З міста А до міста В виїхав вантажний автомобіль, а за годину з А то В виїхав легковий автомобіль. До міста В автомобілі приїхали одночасно. Якщо б з міст А і В автомобілі виїхали одночасно назустріч один одному, то зустріч відбулася б за 1 год 12 хв після їх виїзду. Знайти час, за який проїде шлях від А до В вантажний автомобіль.
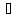 Нехай
вантажний автомобіль проїжджає відстань
від А до В за
Нехай
вантажний автомобіль проїжджає відстань
від А до В за
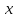 год. Тоді легковий автомобіль проїде
цю відстань за
год. Тоді легковий автомобіль проїде
цю відстань за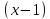 год. Позначимо відстань між містами
через
год. Позначимо відстань між містами
через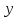 км.
Тоді, згідно з умовами задачі, одержимо
наступне рівняння:
км.
Тоді, згідно з умовами задачі, одержимо
наступне рівняння:

Оскільки
 ,
то
,
то
За
змістом задачі
 .
Отже
.
Отже .
.
Відповідь:
3 год.
Приклад 1.48. Обчислити
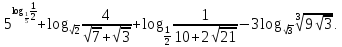
1.

2.
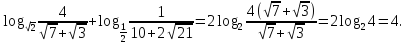
3.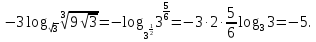
Відповідь:
1.
Приклад
1.49.
Обчислити
 ,
якщо
,
якщо .
.
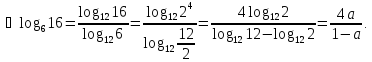
Відповідь:
 .
.
Приклад
1.50.
Обчислити
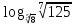 ,
якщо
,
якщо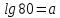 .
.
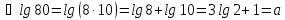 ,
звідки
,
звідки
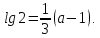
Тоді
 .
.
Відповідь:
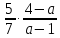 .
.
Приклад
1.51.
Виразити через a
і b
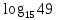 ,
якщо
,
якщо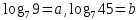 .
.

Відповідь:
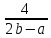 .
.
Приклад
1.52.
Обчислити
 ,
якщо
,
якщо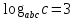 .
.
 Логарифми
визначені, якщо
Логарифми
визначені, якщо
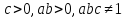 .
При цих обмеженнях маємо:
.
При цих обмеженнях маємо:
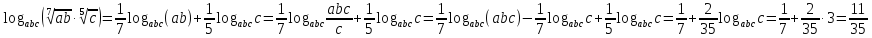 .
.
Відповідь:
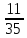 .
.
Приклад
1.53.
Обчислити
 ,
якщо
,
якщо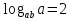 .
.
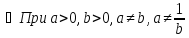 маємо:
маємо:
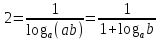 ,
звідки
,
звідки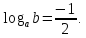 Тому
Тому
Відповідь:
 .
.
Приклад
1.54.
Довести, що
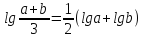 ,
якщо
,
якщо .
.
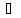 За
умовою
За
умовою

 .
.
Звідки
 .
.
Приклад 1.55. Порівняти числа:
1)
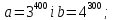
2)

3)
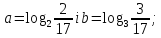
4)
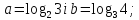
5)
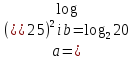 .
.
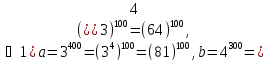
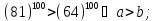
2)
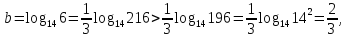
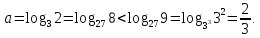
Отже,
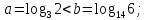
3)
для значення
 виконується нерівність
виконується нерівність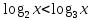 ,
тому
,
тому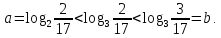
Отже,

4) числа a і b задовольняють нерівності
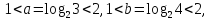
а
числа
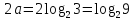 та
та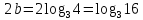 задовольняють нерівності
задовольняють нерівності

Отже,
 ,
тому
,
тому
5) знайдемо різницю даних чисел:
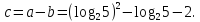
Число
с є значенням квадратного тричлена
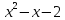 при
при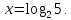
Визначимо
знак:
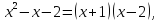 отже,
отже, при
при і
і при
при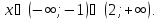
Для
числа
 значення
значення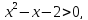 отже,
отже,
Приклад
1.56.
Розв’язати рівняння
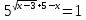 .
.
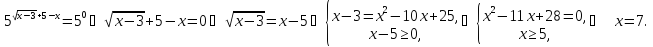
Відповідь:
7.
Приклад
1.57.
Розв’язати рівняння
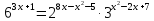 .
.
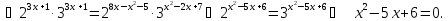
Відповідь:{2;3}.
Приклад
1.58.
Розв’язати рівняння
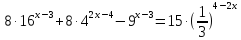 .
.
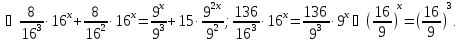
Відповідь:
3.
Приклад
1.59.
Розв’язати рівняння:
 .
.
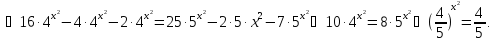
Відповідь: {-1;1}.
Приклад
1.60.
Розв’язати рівняння:
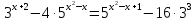 .
.
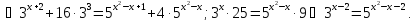
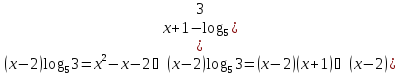
Відповідь:{2,
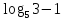 }.
}.
Приклад
1.61.
Розв’язати рівняння:
 .
.
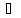 Рівняння
однорідне, оскільки основи показникових
функцій 4, 14 і 49 є послідовними членами
геометричної прогресії:
Рівняння
однорідне, оскільки основи показникових
функцій 4, 14 і 49 є послідовними членами
геометричної прогресії:
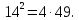

Відповідь:{-1,0,1}.
Приклад
1.62.
Розв’язати рівняння:
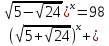 .
.
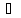 Оскільки
Оскільки

то
після зміни
 рівняння зводиться до квадратного:
рівняння зводиться до квадратного:
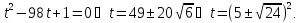
Відповідь:{-4;4}.
Приклад
1.63.
Розв’язати рівняння:
 .
.

Відповідь: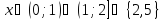 .
.
Приклад
1.64.
Розв’язати рівняння:
 .
.
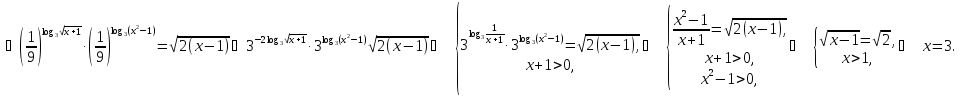
Відповідь:
3.
Приклад
1.65.
Розв’язати нерівність: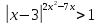 .
.
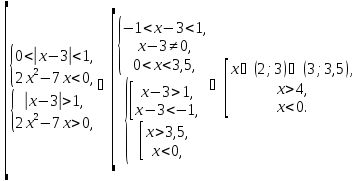
Відповідь: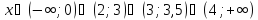 .
.
Приклад
1.66.
Розв’язати нерівність:
 .
.
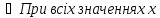
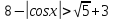
(Oскільки

Тому дана нерівність рівносильна нерівності
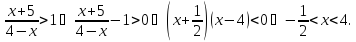
Відповідь:
 .
.
Приклад
1.67.
Розв’язати нерівність:
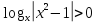 .(*)
.(*)


Відповідь:
 .
.
Приклад
1.68.
Розв’язати нерівність:
 .
.
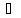 Оскільки
Оскільки
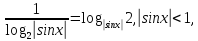
a
 при всіхx,
то
при всіхx,
то
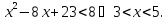
Із
цього інтервалу вилучаємо точки, в яких
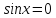 або
або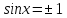 ,
тобто
,
тобто та
та
Відповідь:
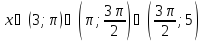 .
.
Приклад 1.69. Для всіх значень параметра а розв’язати нерівність:
 .
.
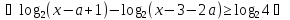

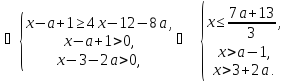
Порівняємо
числа
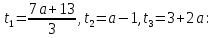
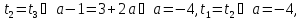
якщо
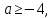 то
то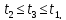 якщо
якщо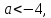 то
то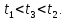
Отже,
при
 система нерівностей має розвязки
система нерівностей має розвязки
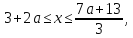 при
при
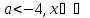 .
.
Відповідь:
 .
.
Розділ 2. Тригонометрія
Приклад
2.1. Довести
тотожність
 .
.
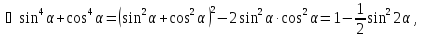
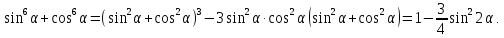
Тому
 ,
що й треба було довести.
,
що й треба було довести.
Приклад 2.2. Довести тотожність
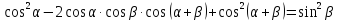 .
.
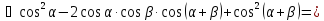
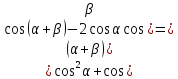

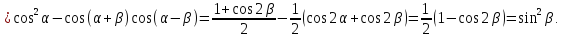
що
й треба було довести.
Приклад
2.3.
Спростити вираз
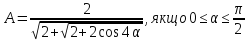 .
.
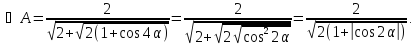
За
умовою
 .
.
Розіб’ємо
цей проміжок на два
 і
і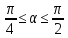 .
.
Тоді
при
 маємо
маємо ,
тому
,
тому
 .
.
При
 маємо
маємо ,
тому
,
тому
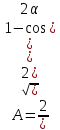 .
.
Відповідь:
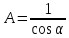 ,
якщо
,
якщо ;
;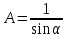 , якщо
, якщо .
.
Приклад
2.4.
Довести, що коли
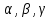 – внутрішні кути трикутника
– внутрішні кути трикутника ,то
справджується рівність
,то
справджується рівність
 .
.
 Спочатку
виключимо кут
Спочатку
виключимо кут
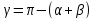 ,
а після перетворень виразу знову
покладемо
,
а після перетворень виразу знову
покладемо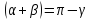 .
.
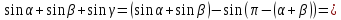
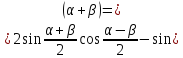
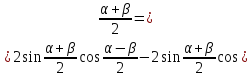
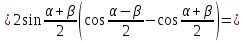
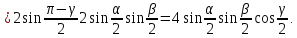
що
й треба було довести.
Приклад
2.5.
Довести рівність
 .
.

що
й треба було довести.
Приклад
2.6.
Обчислити вираз
 .
.

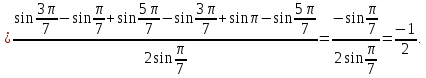
Відповідь:
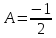 .
.
Приклад
2.7.
Обчислити без таблиць
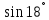 .
.
 Нехай
Нехай
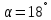 .
Подамо тотожність
.
Подамо тотожність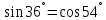 у вигляді
у вигляді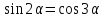 .
Звідси
.
Звідси
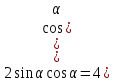 .
.
Оскільки
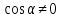 ,
то
,
то
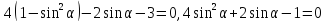 .
.
Знаходимо
додатний
 корінь квадратного відносно
корінь квадратного відносно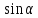 рівняння:
рівняння: .
.
Відповідь:
 .
.
Приклад
2.8.
Обчислити значення виразу
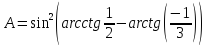 .
.
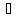 Позначимо
Позначимо
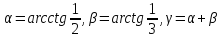 .
Тоді
.
Тоді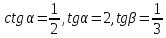 .
Враховуючи непарність арктангенса,
обчислимо
.
Враховуючи непарність арктангенса,
обчислимо
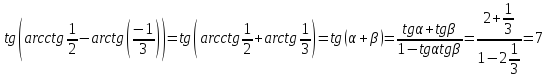 .
За формулою
.
За формулою
 обчислюємо
значення
обчислюємо
значення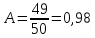 .
.
Відповідь:
0,98.
Приклад
2.9.
Обчислити значення виразу
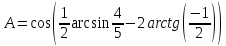 .
.
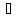 Оскільки
Оскільки
 ,
то
,
то
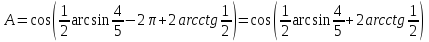 .
.
Нехай
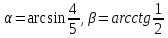 ,
тоді
,
тоді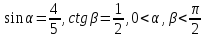 .
.
Отже,
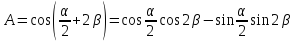 .
.
За формулами подвійного та половинного кутів маємо
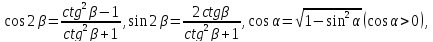
 .
.
Звідси
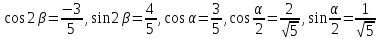 .
.
Отже,
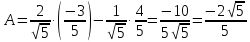 .
.
Відповідь:
 .
.
Приклад
2.10.
Розвязати рівняння
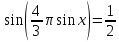 .
.
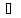 Маємо
Маємо
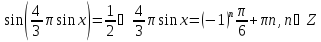 .
Звідки
.
Звідки .
Останнє рівняння має розв’язки лише
за умови
.
Останнє рівняння має розв’язки лише
за умови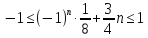 ,
яка виконується лише при
,
яка виконується лише при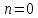 та
та .
При цих значенняхn
дістанемо рівняння
.
При цих значенняхn
дістанемо рівняння
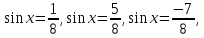 які мають відповідно розвязки
які мають відповідно розвязки
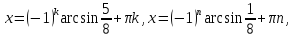
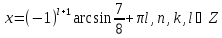 .
.
Відповідь:

Приклад
2.11. Розв’язати
рівняння
 .
.
 Бачимо,
що
Бачимо,
що
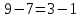 ,
отже, згрупуємо функції і застосуємо
формулу різниці косинусів:
,
отже, згрупуємо функції і застосуємо
формулу різниці косинусів:
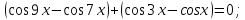
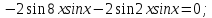
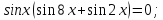
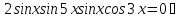
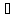


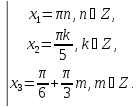
Розв’язок
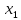 міститься у розв’язку
міститься у розв’язку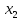 (при
(при ).
Рівняння ж
).
Рівняння ж – не має цілих розв’язків.
– не має цілих розв’язків.
Відповідь:
 .▼
.▼
Приклад
2.12. Розв’язати
рівняння
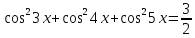 .
.
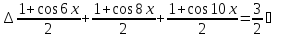
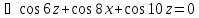 ;
;
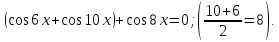
Відповідь:
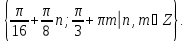 ▼
▼
Приклад 2.13. Розв’язати рівняння
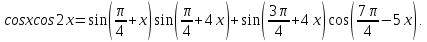
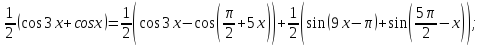
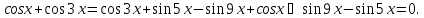
Відповідь:
 ▼
▼
Приклад
2.14. Розв’язати
рівняння
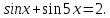
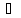 Оскільки
Оскільки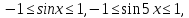 то
то
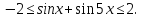
Отже, рівняння рівносильне системі
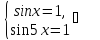
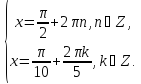
Система
має розв’язки лише тоді, коли рівняння
 має розв’язки на множині цілих чисел.
У цьому випадку маємо розв’язки
має розв’язки на множині цілих чисел.
У цьому випадку маємо розв’язки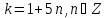 тому
тому
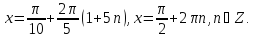
Відповідь:
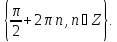 ▼
▼
Приклад
2.15. Розв’язати
рівняння
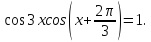 (*)
(*)
 Рівняння
(*) рівносильне сукупності
Рівняння
(*) рівносильне сукупності
 або
або
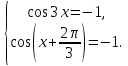
Розв’яжемо першу систему рівнянь

Аналогічно знаходимо розв’язки другої системи
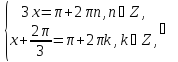

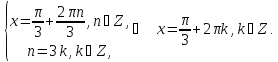
Відповідь:
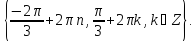 ▼
▼
Приклад
2.16.
Розв’язати рівняння

 Рівняння
рівносильне сукупності систем
Рівняння
рівносильне сукупності систем
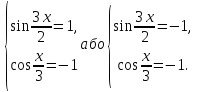
Знаходимо розв’язки цих систем:

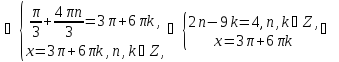

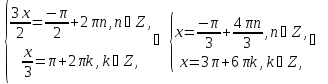
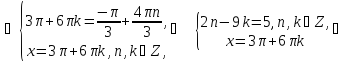
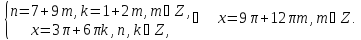
Відповідь:
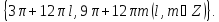 ▼
▼
Приклад
2.17. Розв’язати
рівняння
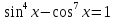 .
.
∆ Оскільки
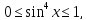 то
то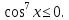 Отже, дане рівняння матиме вигляд
Отже, дане рівняння матиме вигляд
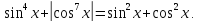
Проте
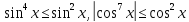 ,
тому ця рівність виконуватиметься лише
тоді, коли
,
тому ця рівність виконуватиметься лише
тоді, коли
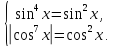
Отже,
можливі два випадки
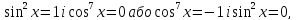
звідки

Відповідь:
 ▼
▼
Приклад
2.18.
Розв’язати рівняння

∆

Відповідь:
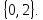 ▼
▼
Приклад
2.19. Розв’язати
рівняння

∆ ОДЗ:
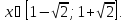
Виразимо арккосинус через арксинус:
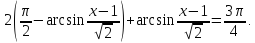
Дістанемо
рівняння
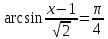 ,звідки
,звідки
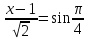 і
і
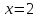 .
.
Відповідь: {2}. ▼
Приклад
2.20. Розв’язати
рівняння
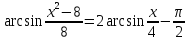 .
.
∆ОДЗ:
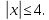
Нехай
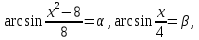 тоді
тоді причому
причому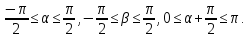
Із
рівняння маємо
 Обчислимо косинус від обох частин
рівняння:
Обчислимо косинус від обох частин
рівняння:
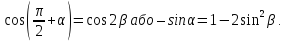
Підставимо
значення
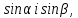 дістанемо тотожність
дістанемо тотожність

Відповідь:
 ▼
▼
Приклад
2.21. Розв’язати
систему рівнянь

∆Система рівносильна сукупності двох систем
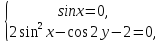 або
або

Перша система роз’язків не має.
Розв’язуємо другу систему рівнянь:
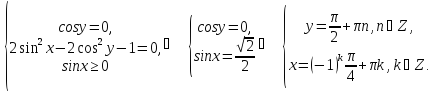
Відповідь:
 ▼
▼
Приклад
2.22. Для
кожного значення параметра
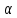 розв’язати рівняння
розв’язати рівняння
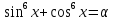 .
.
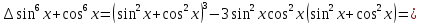
 .
.
Тому
 ,
звідки
,
звідки .
.
Це
рівняння має розв’язки
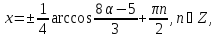 якщо
якщо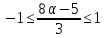 ,
тобто
,
тобто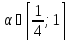 .
.
При
інших значеннях параметра
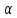 розв’язків немає.
розв’язків немає.
Відповідь:
якщо
 ,
то розв’язків немає, якщо
,
то розв’язків немає, якщо ,
то
,
то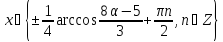 .
▼
.
▼
Приклад
2.23. Знайти
всі значення параметра
 ,
при кожному з яких рівняння
,
при кожному з яких рівняння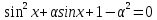 має розв’язки? Знайти ці розв’язки.
має розв’язки? Знайти ці розв’язки.
 Заміною
Заміною ,
зведемо дане рівняння до квадратного:
,
зведемо дане рівняння до квадратного:
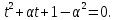
Тригонометричне
рівняння має розв’язки при тих значеннях
параметра
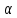 ,
при яких квадратне рівняння має принаймні
один розв’язок на проміжку
,
при яких квадратне рівняння має принаймні
один розв’язок на проміжку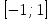 .
Дискримінант квадратного тричлена
.
Дискримінант квадратного тричлена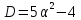 ,
його корені при
,
його корені при
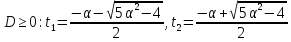 .
.
Розглянемо такі випадки.
Обидва корені квадратного тричлена
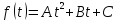 належать проміжку
належать проміжку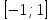 ,
якщо:
,
якщо: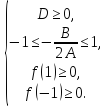
Маємо
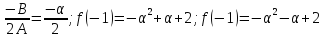 ,
тому
,
тому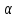 визначаємо з системи:
визначаємо з системи:


Для
цих значень
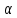 дістанемо розв’язки тригонометричного
рівняння:
дістанемо розв’язки тригонометричного
рівняння:
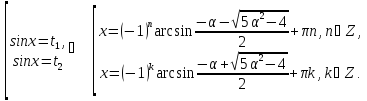
Один із коренів квадратного тричлена належить проміжку
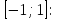
а)
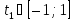 ,
а
,
а
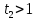 ,
якщо
,
якщо

У
цьому випадку рівняння
 має
розв’язки
має
розв’язки

б)
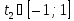 ,
а
,
а
 ,
якщо
,
якщо

У
цьому випадку рівняння
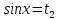 має розв’язки
має розв’язки
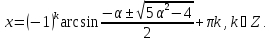
Для
решти значень параметра
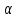 рівняння не має розв’язків.
рівняння не має розв’язків.
Відповідь:
якщо
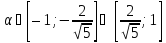 ,
то
,
то
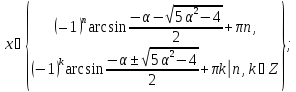
якщо
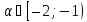 ,
то
,
то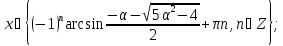
якщо
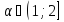 ,
то
,
то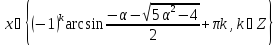 .
▼
.
▼
Приклад
2.24. Знайти
всі значення параметра
 ,
при кожному з яких рівняння
,
при кожному з яких рівняння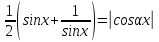 має
розв’язки? Знайти ці розв’язки.
має
розв’язки? Знайти ці розв’язки.
 Права
частина рівняння невід’ємна, причому
Права
частина рівняння невід’ємна, причому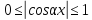 .
Тому ліва частина також невід’ємна,
тобто
.
Тому ліва частина також невід’ємна,
тобто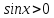 .
Зауважимо, що в цьому випадку
.
Зауважимо, що в цьому випадку
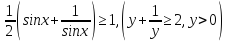 .
.
Рівність обох частин рівняння можлива лише у випадку, коли
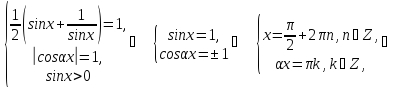
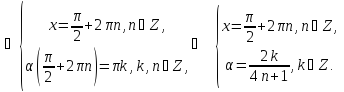
Для
решти значень параметра
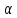 рівняння не має розв’язків.
рівняння не має розв’язків.
Відповідь:
при
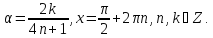
Приклад
2.25. Знайти
всі значення параметра
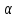 ,
при кожному з яких рівняння
,
при кожному з яких рівняння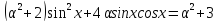 має розв’язки? Знайти ці розв’язки.
має розв’язки? Знайти ці розв’язки.
 Рівняння
зводиться до однорідного:
Рівняння
зводиться до однорідного:
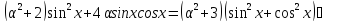
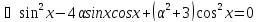 .
.
Переконуємося,
що
 ,
поділимо на
,
поділимо на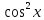 ,
дістанемо рівняння
,
дістанемо рівняння
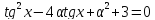 .
.
Заміною
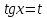 рівняння зводиться до квадратного
рівняння зводиться до квадратного

Це
рівняння має розв’язки, якщо
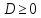 ,
тобто
,
тобто
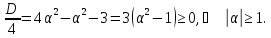
Отже,
якщо
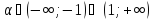 ,
то
,
то

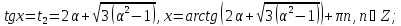
якщо
 ,
то
,
то
якщо
 ,
то
,
то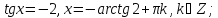
якщо
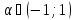 то розв’ків не має.
то розв’ків не має.
Відповідь:
якщо
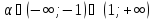 ,
то
,
то
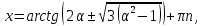
якщо
 ,
то
,
то
якщо
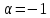 ,
то
,
то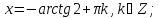
якщо
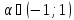 то розв’ків не має.
то розв’ків не має.
Приклад
2.26. Знайти
всі значення параметра
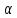 ,
при кожному з яких рівняння
,
при кожному з яких рівняння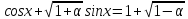 має розв’язки? Знайти ці розв’язки.
має розв’язки? Знайти ці розв’язки.
 ОДЗ:
ОДЗ:
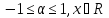 .
Запроваджуємо допоміжний кут:
.
Запроваджуємо допоміжний кут:

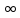 Із
множини розв’язків першого рівняння
лише значення
Із
множини розв’язків першого рівняння
лише значення
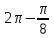 належить проміжку
належить проміжку .
Друге рівняння має розв’язки за умови
.
Друге рівняння має розв’язки за умови .
Зауважимо, що функція
.
Зауважимо, що функція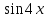 має період
має період ,
тому на проміжку
,
тому на проміжку довжини періоду друге рівняння може
мати: один розв’язок, якщо
довжини періоду друге рівняння може
мати: один розв’язок, якщо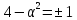 ,
тобто
,
тобто
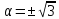 ,
або
,
або
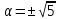 (у цьому випадку розв’язки обох рівнянь
збігаються); два розв’язки, якщо
(у цьому випадку розв’язки обох рівнянь
збігаються); два розв’язки, якщо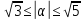 і
і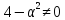 ;
три розв’язки, якщо
;
три розв’язки, якщо .
.
Отже,
рівняння матиме рівно чотири різних
розв’язки на проміжку
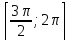 ,
якщо
,
якщо .
.
Відповідь:
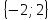 .
▼
.
▼
Приклад
2.29. Знайти
всі значення параметра
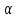 ,
при кожному з яких рівняння
,
при кожному з яких рівняння має єдиний розв’язок? Знайти цей
розв’язок.
має єдиний розв’язок? Знайти цей
розв’язок.
 Функція
Функція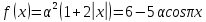 при всіх значеннях параметра
при всіх значеннях параметра є парною щодо
є парною щодо .
.
Якщо
число
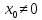 є розв’язком даного рівняння, то
є розв’язком даного рівняння, то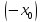 також буде розв’язком. Отже, єдиним
може бути лише розв’язком
також буде розв’язком. Отже, єдиним
може бути лише розв’язком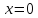 .
Знайдемо значення параметра
.
Знайдемо значення параметра ,
при яких рівняння не має інших розв’язків,
крім
,
при яких рівняння не має інших розв’язків,
крім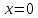 .
.
Підставимо
значення
 у рівняння, дістанемо квадратне рівняння
у рівняння, дістанемо квадратне рівняння
 ,
яке має корені
,
яке має корені
 і
і .
.
Якщо
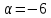 ,
то дане рівняння матиме вигляд
,
то дане рівняння матиме вигляд
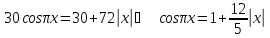 .
.
Це
рівняння інших коренів, крім
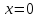 ,
не має, оскільки
,
не має, оскільки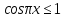 ,
а
,
а
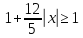 при
при
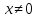 .
.
Якщо
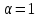 ,
то дане рівняння має вигляд
,
то дане рівняння має вигляд
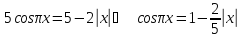 .
.
і
може мати корені, крім
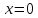 ,
наприклад,
,
наприклад,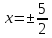 .
.
Тому
значення
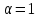 не справджує умову задачі.
не справджує умову задачі.
Відповідь:
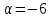 ,
, .▼
.▼
Приклад
2.30. Знайти
всі значення параметра
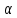 ,
при кожному з яких система рівнянь
,
при кожному з яких система рівнянь
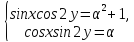 має
розв’язки? Знайти ці розв’язки.
має
розв’язки? Знайти ці розв’язки.
 Якщо
Якщо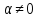 ,
то перше рівняння системи не має
розв’язків, оскільки
,
то перше рівняння системи не має
розв’язків, оскільки
 ,
а
,
а
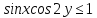 .
Знайдемо розв’язки системи, якщо
.
Знайдемо розв’язки системи, якщо
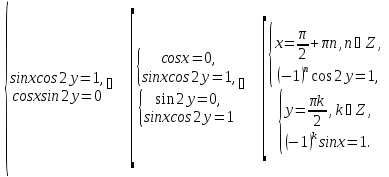
Рівняння
 має розв’язки
має розв’язки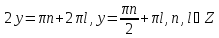 .
.
Рівняння
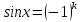 має розв’язки
має розв’язки .
.
Розв’язки обох систем збігаються.
Відповідь:
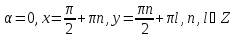 .
▼
.
▼
Приклад
2.31. Розв’язати
нерівність
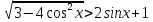 .
.
 Дана
нерівність рівносильна сукупності двох
систем нерівностей
Дана
нерівність рівносильна сукупності двох
систем нерівностей
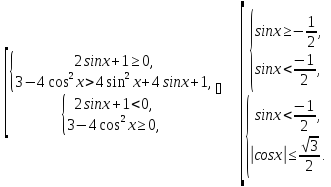
Перша
– несумісна. Знаходимо розв’язки другої

Перша
нерівність має розв’язки
 а друга:
а друга:
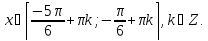 Знаходимо
перетин цих множин.
Знаходимо
перетин цих множин.
Відповідь:
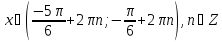 .▼
.▼
Приклад
2.32. Розв’язати
нерівність
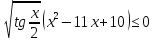 .
.
 Нерівність
рівносильна сукупності:
Нерівність
рівносильна сукупності:
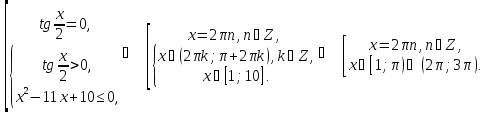
Відповідь:
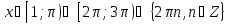 .
▼
.
▼
Приклад
2.33. Розв’язати
нерівність
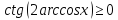 .
.
 Знаходимо
розв’язок тригонометричної нерівності:
Знаходимо
розв’язок тригонометричної нерівності:
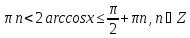 .
.
звідки
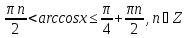 .
.
Проте
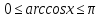 ,
тому при значеннях
,
тому при значеннях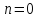 та
та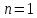 розв’язуємо нерівності
розв’язуємо нерівності та
та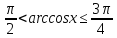 .
Для цього беремо косинус від усіх частин
нерівностей. Враховуючи, що на інтервалі
.
Для цього беремо косинус від усіх частин
нерівностей. Враховуючи, що на інтервалі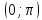 косинус спадає, дістаємо
косинус спадає, дістаємо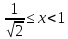 та
та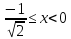 .
.
Відповідь:
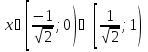 .
▼
.
▼
Приклад
2.34. Розв’язати
нерівність
 .
.
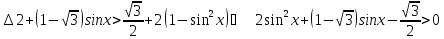
Зробимо
заміну
 ,
тоді
,
тоді
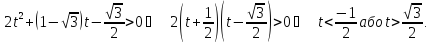
Отже,
маємо сукупність нерівностей

Знаходимо її розв’язок:

Відповідь:
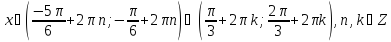 .▼
.▼
Приклад
2.35. Розв’язати
нерівність
 .
.
 Зведемо
її до однорідної:
Зведемо
її до однорідної:
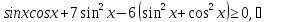

Якщо
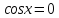 ,
то нерівність
,
то нерівність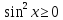 завжди виконується. Якщо
завжди виконується. Якщо ,
то поділимо нерівність на
,
то поділимо нерівність на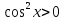 ,
дістанемо
,
дістанемо
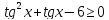 .
.
Алгебраїчна
відносно
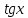 нерівність має розв’язки
нерівність має розв’язки
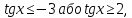
а тому:

Доповнимо
ці інтервали розв’язками рівняння
 ,
тобто множиною
,
тобто множиною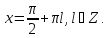
У відповіді записуємо об’єднання цих множин розв’язків.
Відповідь:
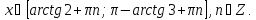 ▼
▼
Приклад
2.36. Розв’язати
нерівність
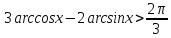 .
.
 Нерівність
визначена при
Нерівність
визначена при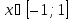 .
Оскільки
.
Оскільки
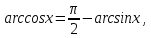
то
маємо
 ,
звідки
,
звідки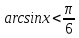 .
.
За
означенням
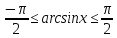 маємо рівносильну нерівність
маємо рівносильну нерівність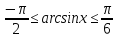 .
.
Беремо
синус від усіх частин нерівності (на
інтервалі
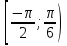 синус зростає),
синус зростає),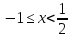 .
.
Відповідь:
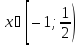 .▼
.▼
Приклад
2.37. Для
всіх значень параметра
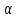 розв’язати нерівність
розв’язати нерівність
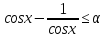 .
.
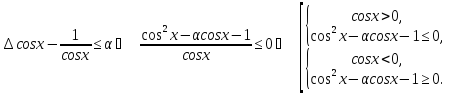
Розв’яжемо першу систему нерівностей:
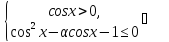
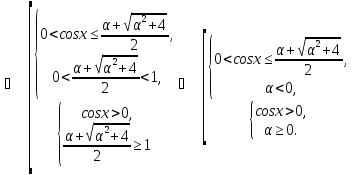
Отже,
якщо
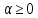 ,
то
,
то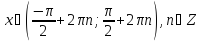 ;
якщо
;
якщо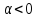 :
:
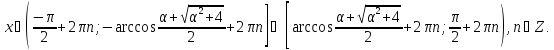
Знайдемо розв’язок другої системи нерівностей:
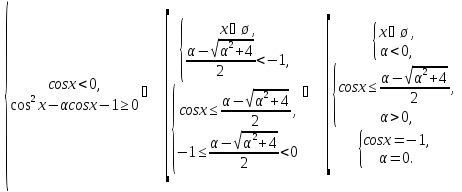
Отже, ця система нерівностей має такі розв’язки:
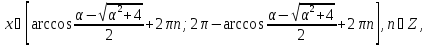
якщо
 якщо
якщо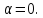
Відповідь:
якщо
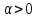 ,
то
,
то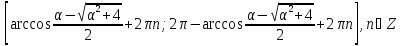 ;
;
і
 ;
;
якщо
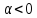 ,
то
,
то
якщо
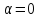 ,
то
,
то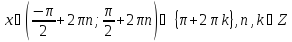 .
▼
.
▼
Приклад
2.38.
Знайти
всі значення параметра a,
при
кожному з яких нерівність
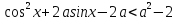 справджується
при всіх дійсних значеннях x.
справджується
при всіх дійсних значеннях x.
Нехай
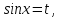 після
введення зміни
після
введення зміни
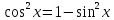 дістанемо
рівносильну систему
дістанемо
рівносильну систему
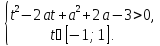 Функція
Функція
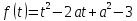 набуває
додатних значень на
набуває
додатних значень на
 у
таких випадках:
у
таких випадках:
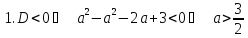

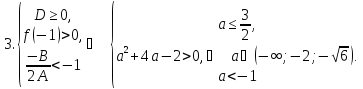
Відповідь: