1

История логики изучает развитие науки о формах и законах правильного мышления (логика).

Появление логики в качестве разработанного анализа принципов умозаключений имеет отношение исключительно к трём локальным цивилизациям, а именно: Китай, Индия и Древняя Греция. Из них только трактовка логики в древнегреческой философии, детально рассмотренная в сочинении Аристотеля «Органон», принята и нашла широкое применение в современной науке и математике. В Древней Греции логика была известна как диалектика или аналитика.

В дальнейшем логика Аристотеля была развита исламскими и затем средневековыми европейскими логиками, и наибольшего подъёма достигла в середине XIV века. С XIV века до начала XIX века логика находилась в упадке, историки логики считают этот период непродуктивным.

2

Логические теории – основные понятия, состав и задачи теорий

Логическая теория — это концептуальный класс элементарных высказываний, описывающих свойства и связи определённой области логических исчислений (см.: Логика). Логическую теорию также отождествляют со способом выбора подкласса истинных высказываний (теорем) из числа высказываний, сформулированных на языке данной теории. В самом общем виде логическая теория рассматривается как множество утверждений, замкнутых относительно выводимости, задающей способ выбора теорем..

Первый поход с самого начала рассматривает теорию как детерминированную определённым классом моделей и интерпретацией на этих моделях. Второй подход рассматривает теорию как определяемую:

• категорией различных словарей — наборов атомарных формул;

• функтором, сопоставляющим этой категории категорию предложений, сформулированных на основе этих словарей;

• функтором, сопоставляющим категории словарей категорию моделей, то есть семантических эквивалентов предложений;

• функцией выполнимости, сопоставляющей каждому словарю бинарное отношение L логической выполнимости между объектами категории моделей и объектами категории предложений.

3Схемы важнейших законов логики предикатов.

Как и в JIB, в логике предикатов существуют логически истинные формулы, называемые тавтологиями или законами ЛП. Ниже приводятся и комментируются наиболее важные.

Закон удаления квантора общности

Общее правило, истинное для каждого ? должно быть истинно и для отдельного случая а, являющегося элементом расширения формулы Если истинно высказывание «Все вещи универсума круглые», то должно быть истинно высказывание «Вещь по имени а, принадлежащая универсуму, является круглой»:

Закон введения квантора существования

То, что истинно для отдельного случая а, являющегося элементом расширения формулы должно быть истинно в качестве произвольного примера подстановки предметной переменной ? формулы ф?. Из истинности высказывания «Вещь а, принадлежащая универсуму, является круглой» следует истинность высказывания «Существует такая ? что истинно „? — круглая"»:

Закон подчинения кванторов

Из истинности универсально квантифицированнош высказывания следует истинность экзистенциально квантифицированного высказывания; из ложности экзистенциально квантифицированного высказывания следует ложность универсально квантифицированного высказывания:

Закон противоречия

Противоречащие друг другу высказывания не могут быть вместе ни истинны, ни ложны:

Закон непустоты универсума логического квадрата

В универсуме логического квадрата должна существовать хотя бы одна вещь, выполняющая формулу ф% или ее отрицание —іф% (или и то и другое):

Законы взаимоопределимости кванторов

Каждый квантор может быть определен в терминах противоположного ему квантора: Законы дистрибутивности кванторов

относительно знака конъюнкции

Квантор общности дистрибутивен относительно знака конъюнкции без ограничений:

Квантор существования дистрибутивен относительно знака конъюнкции с ограничением:

НШФЄ& <р4) => т<р&

Законы дистрибутивности кванторов

относительно знака дизъюнкции

Квантор общности дистрибутивен относительно знака дизъюнкции с ограничением:

Квантор существования дистрибутивен относительно знака дизъюнкции без ограничений:

Законы дистрибутивности кванторов

относительно знака импликации

Из высказывания «Для каждого числа, если оно — четное, то оно — целое» выводимо высказывание «Если каждое число четное, то каждое число целое».

Но обратная выводимость в общем неверна:

Из высказывания «Если существует четное число, то существует целое число» выводимо высказывание «Существует такое число, что если оно четное, то оно целое». Но обратная выводимость в общем неверна:

I- [(??#=> (Е$<РЗ З <Р&

Из высказывания «Существует такое число, что если оно четное, то оно целое» выводимо высказывание «Если каждое число четное, то существует целое число». Но обратная выводимость в общем неверна:

I- гё) з

Из высказывания «Если существует четное число, то все числа целые» выводимо высказывание «Для каждого числа, если оно — четное, то оно — целое». Но обратная выводимость в общем неверна:

Из сказанного следует, что кванторы общности и существования дистрибутивны относительно знака импликации лишь с ограничением.

Законы перестановки кванторов

Кванторы общности и существования могут переставляться в любом порядке, если они предшествуют формуле однородно, т. е. либо только кванторы общности, либо только кванторы существования. В противном случае имеет место ограничение: независимый квантор существования может свободно вводиться в область действия квантора общности, но не может из нее свободно выводиться.

5Алфавит языка логики высказываний, понятие формулы.

Язык логики высказываний

Язык логики высказываний (пропозициональный язык^[4]) — искусственный язык, предназначенный для анализа логической структуры сложных высказываний^[1].

Алфавит языка логики высказываний

Исходные символы, или алфавит языка логики высказываний, разделены на следующие три категории^[1][5]:

• пропозициональные буквы (пропозициональные переменные):

• логические знаки (логические союзы):

Символ	Значение
	Знак отрицания
	Знак конъюнкции («И»)
	Знак дизъюнкции («включающее ИЛИ»)
	Знак строгой дизъюнкции («исключающее ИЛИ»)
	Знак импликации
	Знак эквивалентности

• технические знаки:

Символ	Значение
	Левая скобка
	Правая скобка

Других знаков в алфавите языка логики высказываний нет.

Пропозициональные переменные

Пропозициональная переменная — переменная, которая в пропозициональных формулах служит для замены собой элементарных логических высказываний^[3].

Пропозициональные формулы

Роль структурных образований, аналогичных элементарным и сложным высказываниям, играют в этом языке формулы. Пропозициональная формула — конечная последовательность знаков алфавита, построенная по изложенным ниже правилам и образующая законченное выражение языка логики высказываний^[1]. Заглавные латинские буквы , и другие, которые употребляются в определении формулы, принадлежат не языку логики высказываний, а его метаязыку, то есть языку, который используется для описания самого языка логики высказываний. Содержащие метабуквы выражения , и другие — не пропозициональные формулы, а схемы формул. Например, выражение есть схема формул , и другие^[1].

Индуктивное определение формулы логики высказываний:^[4][1]

1. пропозициональная переменная есть формула;

2. если  — произвольная формула, то 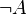 — тоже формула;

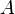3. если и 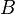 — произвольные формулы, то , , 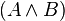, 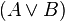и  — тоже формулы.

Других формул в языке логики высказываний нет.

Относительно любой последовательности знаков алфавита языка логики высказываний можно решить, является она формулой или нет. Если эта последовательность может быть построена в соответствии с пп. 1—3 определения формулы, то она формула, если нет, то не формула^[1].

Язык логики высказываний можно рассматривать как множество пропозициональных формул^[4].

Для формул логики высказываний можно определить понятие интерпретации как приписывание каждой пропозициональной переменной истинностного значения^[6] («истина» или «ложь», хотя исчисление высказываний никак не ограничивает множество возможных значений при интерпретации: например, можно задать интерпретацию как отображение в множество , где , — такой подход может использоваться, к примеру, при доказательстве независимости схем аксиом исчисления высказываний).

Пусть – некоторое множество логических переменных. По индукции определим понятие формулы алгебры логики:

1) любая логическая переменная является формулой (атомарной);

2) если и – формулы, то выражения и другие, представленные в табл. 1, являются формулами;

3) никаких других формул, кроме построенных в пунктах 1 и 2, нет.

6

Определение значений формул логики высказываний и логических отношений между формулами.

Формулы множества D называются совместимыми по истинности, если и только если существует такая интерпретация входящих в эти формулы пропозициональных переменных, при которой формулы данного множества принимают значение «истина». В противном случае данные формулы несовместимы по истинности. Формулы множества D называются совместимыми по ложности, если и только если существует такая интерпретация входящих в них пропозициональных переменных, при которой все формулы данного множества принимают значение «ложь».

 Отношение логического следования: из множества формул D логически следует формула В, если и только если при всех интерпретациях, при которых истинны (имеют модели) все формулы множества D, истинна также (имеет модель) формула В. Т.е. не существует ни одной интерпретации, при которой формулы множества D были бы истинны, а формула В при этом была бы ложна. Обозначается {D}=>B . Например: все студенты балдежники, некоторые студенты балдежники. Из первого здесь логически следует второе. Формулы Х и Y являются логически эквивалентными, если и только если X=>Y, Y=>X (например: p->q, ), т.е. принимают одинаковые логические значения. Формулы X и Yнаходятся в отношении контродикторности, если и только если они не совместимы ни по истинности, ни по ложности, как например P и . Между X и Yимеет место отношение субконтродикторности, если и только если формулы не совместимы по истинности. Например: . Формулы X и Y логически независимы, если и только если они совместимы по истинности, по ложности и из

7 АНАЛИТИЧЕСКИХ ТАБЛИЦ МЕТОД — разрешающий метод для проблемы общезначимости формул классической, интуиционистской и модальной (система S4) логики высказываний. В сочетании с некоторыми дополнительными приемами этот метод применим и для классической и интуиционистской логики предикатов. В последнем случае метод аналитических таблиц представляет собой полуразрешающую процедуру, поскольку положительное решение вопроса об общезначимости достижимо для любой общезначимой формулы, а отрицательное — не для всякой необщезначимой формулы. Так как к вопросу об общезначимости формул сводятся вопросы о наличии логического следования, а также несовместимости по истинности (ложности) формул языков соответствующих логических систем, то аналитические таблицы применимы и для решения этих вопросов.     Построение аналитической таблицы для некоторой формулы А начинается с предположения о ее ложности. Далее по правилам построения осуществляется сведение этого предположения к все более простым условиям ложности А в виде выражений ТВ (“истинно В”) и FB (“ложно В”), называемых отмеченными формулами (далее “ТГ — формулы”), где В— формула соответствующей системы. В случае общезначимости А процесс редукции приводит к противоречию.

8

Предваренные нормальные формы, примеры построения.

Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отнесена к элементарным формулам.      Очевидно, что, используя равносильности алгебры высказываний и логики предикатов, каждую формулу логики предикатов можно привести к нормальной формуле. 

Среди нормальных форм формул логики предикатов важное значение имеют так называемые предваренные нормальные формы (п.н.ф.). В них кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики, то есть предваренная нормальная форма формулы логики предикатов имеет вид:

Теорема. Всякая формула логики предикатов может быть приведена к предваренной нормальной форме.      Доказательство. Будем считать, что формула уже приведена к нормальной форме и покажем, что ее можно привести к предваренной нормальной форме.      Если данная формула является элементарной, то она кванторов не содержит, и, следовательно, уже имеет предваренную форму. 

F=$x"y((P21.(х; y)ÚùP2.(х))&P3(y)) формула, приведенная к ПНФ; F="x(P21.(х; y)Ú$x(P2 (х))&$y(P3 (y)) формула, неприведенная к ПНФ.

"x(P1.(х)) &"x(P2(x))="x(P1.(х) &P2(x)) слева от знака равенства формула, неприведенная к ПНФ, а справа, равносильная ей формула, но приведенная к ПНФ.

Процедура приведения произвольной формулы логики предикатов к предваренной нормальной форме включает следующие шаги:

Преобразование формул, устраняющее логические связки ® и «.

Пронесение отрицания вглубь подформул, чтобы отрицания находились только над атомами.

Вынесение кванторов за скобки в порядке их следования в формуле с учетом общезначимых эквивалентностей логики предикатов.

При необходимости переименование связанных переменных в подформулах во избежание коллизии переменных.

Представление полученной бескванторной формулы в КНФ.

Пример приведения формулы логики предикатов к ПНФ.

9 Понятие метаязыка, схемы важнейших законов логики высказываний.

• Закон тождества: если х, то х, т.е. х → х.

• Закон упрощения: если х и у, то х, т.е. х Ù у →х. То же самое относится к другому конъюнктивному члену:

x Ù y → y

• Закон эквивалентности: если из х следуету, а из у следует х, тогда высказывания эквивалентны, т.е.

x ↔ y.

• Закон гипотетического силлогизма:если из х следует у, а из у следует z, то из хследует z, т.е.

((x → y) Ù (y → z)) → (x → z)

• Закон двойного отрицания: если из х следует не-х, то отрицание последнего приводит к первоначальному высказыванию:

¬ (¬x) ↔ x

• Законы О. де Моргана дают возможность переходить от конъюнкции к дизъюнкции и, наоборот, от дизъюнкции к конъюнкции. Они служат удобным средством для преобразования высказываний:

а) отрицание конъюнкции высказываний эквивалентно дизъюнкции из отрицаний конъюнктивных членов:

¬ (x Ù y) ↔ (¬x Ú ¬y)

б) отрицание дизъюнкции эквивалентно конъюнкции отрицаемых членов дизъюнкции:

¬ (x Ú y) ↔ (¬x Ù ¬y)

• Закон "поглощения": конъюнкция или дизъюнкция одинаковых высказываний эквивалентна самому высказыванию, т.е. повторяющийся член "поглощается":

(x Ùx) → x и (x Ú x) → x.

• Коммутативные законы для конъюнкции и дизъюнкции разрешают перестановку их членов:

(x Ù y) ↔ (x Ù y) и (x Ú y) ↔ (y Ú x).

• Ассоциативные законы для конъюнкции и дизъюнкции позволяют по-разному сочетать члены, т.е. по-иному расставлять скобки:

x Ù (y Ù z) ↔ (x Ù y) Ù z или x Ú (y Ú z) ↔ (x Ú y) Ú z.

• Закон контрапозиции разрешает прямую импликацию заменять обратной, в результате чего антецедент первой заменяется отрицанием консеквента второй, а ее консеквент – отрицанием антецедента. Проще говоря, при контрапозиции происходит перестановка членов импликации или их контрапозиция, но они берутся с отрицаниями:

(x → y) ↔ (¬y → ¬x)

• Закон противоречия: два противоречащих друг другу высказывания, т.е. высказываниех и его отрицание не-х, не могут быть вместе истинными:

(x Ù ¬x)

Поскольку этот закон запрещает противоречия в рассуждении, то его часто называют также законом непротиворечия, и последнее более правильно.

• Закон наслюненного третьего:из двух противоречащих друг другу высказываний только одно является истинным. Тогда второе будет ложным и никакой третьей возможности не существует

Метаязы́к — язык, предназначенный для описания языка.

Понятие метаязыка используется:

• в лингвистике, при описании естественных языков — метаязык как язык для описания языка. Естественный язык может являться своим же метаязыком (например, для описания русского языка можно использовать тот же русский язык), или отличаться лишь частично, например специальной терминологией (русская лингвистическая терминология — элемент метаязыка для описания русского языка);

• в классической философии — как понятие, фиксирующее логический инструментарий рефлексии над феноменами семиотического ряда;

  • в философии постмодернизма, при выражении процессуальности вербального продукта рефлексии над процессуальностью языка. Постмодернистская трактовка метаязыка восходит к работе Р. Барта «Литература и метаязык» (1957).

• при исследовании языков различных логико-математических исчислений (напр., Форма Бэкуса — Наура);

• в информатике — доп. данные (метаданные), служащие для описания имеющихся.

Понятие «метаязык» было введено польским математиком Альфредом Тарским. C помощью него можно избавиться от таких логических парадоксов, как парадокс лжеца и самореферентные парадоксы.

Первым уровнем (обычным языком) являются утверждения об объектах, например: «У Земли есть спутник». В языке низшей ступени нет понятий «ложь» и «истина». Такие понятия, как оценка истинности утверждений об объектах, являются привилегией метаязыка — следующей ступеньки лестницы. Таким образом предложение «Утверждение „снег белый“ истинно» имеет смысл в метаязыке. Однако о его истинности можно говорить лишь в следующей надстройке — метаметаязыке. При этом метаязык является объектным языком для этой следующей ступени. Можно построить метаязык, для которого метаязык будет объектным и т. д.

Другой пример лестницы утверждений и метаязыков:

1. Сумма внутренних углов любого треугольника равна 180°

2. Утверждение 1 истинно.

3. Утверждение 2 истинно.

4. Утверждение 3 истинно.

Здесь первое утверждение написано на языке первого уровня, который позволяет формулировать теоремы планиметрии. Языком второго уровня (фраза № 2) пользуются при доказательстве теорем. Метаметаязык, которому принадлежит третье утверждение, — это язык, на котором написаны книги о теории доказательств.

С лестницей метаязыков Тарского тесно связана теория типов Бертрана Рассела.

10.Формы правильных умозаключений в логике высказываний

По составу все умозаключения делятся на простые и сложные. Простыми называются умозаключения, элементы которых не являются умозаключениями. Сложными называют умозаключения, состоящие из двух или более простых умозаключений.

По количеству посылок умозаключения делятся на непосредственные (из одной посылки) и опосредованные (из двух и более посылок).

По характеру логического следования все умозаключения делятся на необходимые (демонстративные) и правдоподобные (недемонстративные, вероятные). Необходимые умозаключения - такие, в которых истинное заключение обязательно следует из истинных посылок (т. е. логическое следование в таких выводах представляет собой логический закон). К необходимым умозаключениям относятся все виды дедуктивных умозаключений и некоторые виды индуктивных («полная индукция»).

Правдоподобные умозаключения - такие, в которых заключение следует из посылок с большей или меньшей степенью вероятности. Например, из посылок: «Студенты первой группы первого курса сдали экзамен по логике», «Студенты второй группы первого курса сдали экзамен по логике» и т. п. следует «Все студенты первого курса сдали экзамен по логике» с большей или меньшей степенью вероятности (что зависит от полноты наших знаний обо всех труппах студентов первого курса). К правдоподобным умозаключениям относятся индуктивные и умозаключения по аналогии.

Дедуктивное умозаключение (от лат. deductio - выведение) - такое умозаключение, в котором переход от общего знания к частному является логически необходимым.

Путем дедукции получаются достоверные выводы: если истинны посылки, то будут истинны и заключения.

Пример:

Если человек совершил преступление, то он должен быть наказан.

Петров совершил преступление.

Петров должен быть наказан.

Индуктивное умозаключение (от лат. inductio - наведение) - такое умозаключение, в котором переход от частного знания к общему осуществляется с большей или меньшей степенью правдоподобности (вероятности).

Например:

Кража - уголовное преступление.

Грабеж - уголовное преступление.

Разбой — уголовное преступление.

Мошенничество - уголовное преступление.

Кража, грабеж, разбой, мошенничество - преступления против собственности.

Следовательно, все преступления против собственности – уголовные преступления.

Поскольку в основу данного заключения положен принцип рассмотрения не всех, а лишь некоторых предметов данного класса, то умозаключение называется неполной индукцией. Вполной индукции обобщение происходит на основе знаний всех предметов исследуемого класса.

В умозаключении по аналогии (от греч. analogia - соответствие, сходство) на основе сходства двух объектов по каким-то одним параметрам делается вывод об их сходстве по другим параметрам. Например, на основе сходства способов совершения преступлений (кражи со взломом) можно сделать предположение о том, что эти преступления совершались одной и той же группой преступников.

Все виды умозаключений могут быть правильно построенными и неправильно построенными.

11-12 Алгоритмически неразрешимые проблемы

Неразрешимые проблемы и самоприменимые машины Тьюринга

Утверждение о существовании алгоритмически неразрешимых проблем является весьма сильным – мы констатируем, что мы не только сейчас на знаем соответствующего алгоритма, но мы не можем принципиально никогда его найти.

Первой фундаментальной теоретической работой, связанной с доказательством алгоритмической неразрешимости, была работа Курта Гёделя – его известная теорема о неполноте символических логик. Это была строго формулированная математическая проблема, для которой не существует решающего ее алгоритма. Усилиями различных исследователей список алгоритмически неразрешимых проблем был значительно расширен. Сегодня принято при доказательстве алгоритмической неразрешимости некоторой задачи сводить ее к ставшей классической задаче – «задаче останова».

Имеет место быть следующая теорема:

Теорема 3.1. Не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных (и алго-ритм и данные заданы символами на ленте машины Тьюринга) определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.

Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.

Тем не менее, можно попытаться сформулировать причины, ведущие к алгоритмической неразрешимости, эти причины достаточно условны, так как все они сводимы к проблеме останова, однако такой подход позволяет более глубоко понять природу алгоритмической неразрешимости:

а) Отсутствие общего метода решения задачи

Проблема 1: Распределение девяток в записи числа ;

Определим функцию f(n) = i, где n – количество девяток подряд в десятичной записи числа , а i – номер самой левой девятки из n девяток подряд: =3,141592… f(1) = 5.

Задача состоит в вычислении функции f(n) для произвольно заданного n.

Поскольку число является иррациональным и трансцендентным, то мы не знаем никакой информации о распределении девяток (равно как и любых других цифр) в десятичной записи числа . Вычисление f(n) связано с вычислением последующих цифр в разложении , до тех пор, пока мы не обнаружим n девяток подряд, однако у нас нет общего метода вычисления f(n), поэтому для некоторых n вычисления могут продолжаться бесконечно – мы даже не знаем в принципе (по природе числа ) существует ли решение для всех n.

Проблема 2: Вычисление совершенных чисел;

Совершенные числа – это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.

Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вы-числения совершенных чисел, мы даже не знаем, множество совершенных чи-сел конечно или счетно, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность. Отсутствие общего метода решения не позволяет ответить на вопрос о останове алгоритма. Если мы проверили М чи-сел при поиске n-ого совершенного числа – означает ли это, что его вообще не существует?

Проблема 3: Десятая проблема Гильберта;

Пусть задан многочлен n-ой степени с целыми коэффициентами – P, су-ществует ли алгоритм, который определяет, имеет ли уравнение P=0 решение в целых числах?

Ю.В. Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения P=0 по его целочисленным коэффициентам.

б) Информационная неопределенность задачи

Проблема 4: Позиционирование машины Поста на последний помеченный ящик;

Пусть на ленте машины Поста заданы наборы помеченных ящиков (кортежи) произвольной длины с произвольными расстояниями между кортежами и головка находится у самого левого помеченного ящика. Задача состоит установке головки на самый правый помеченный ящик последнего кортежа.

Попытка построения алгоритма, решающего эту задачу приводит к необходимости ответа на вопрос – когда после обнаружения конца кортежа мы сдвинулись вправо по пустым ящикам на М позиций и не обнаружили начало следующего кортежа – больше на ленте кортежей нет или они есть где-то правее? Информационная неопределенность задачи состоит в отсутствии информации либо о количестве кортежей на ленте, либо о максимальном расстоянии между кортежами – при наличии такой информации (при разрешении инфор-мационной неопределенности) задача становится алгоритмически разрешимой.

в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)

Проблема 5: Проблема «останова» (см. теорема 3.1);

Проблема 6: Проблема эквивалентности алгоритмов;

По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных.

Проблема 7: Проблема тотальности;

По произвольному заданному алгоритму определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи – является ли частичный алгоритм Р всюду определённым?

12.

Неразрешимые проблемы и самоприменимые машины Тьюринга

Самопримени́мость в теории алгоритмов — свойство алгоритма успешно завершаться на данных, представляющих собой формальную запись этого же алгоритма.

Задача распознавания самоприменимости является алгоритмически неразрешимой и сводится к тому, чтобы найти алгоритм, позволяющий за конечное число шагов по формальной записи некоего алгоритма узнать, является ли он самоприменимым или нет. Хотя эта задача несколько искусственна и не представляет самостоятельного интереса, но часто используется для того, чтобы доказать неразрешимость других, более сложных задач. Общий метод для подобных выводов состоит в том, что из предположения о существовании алгоритма, решающего некую задачу, выводится существование алгоритма, решающего задачу распознавания самоприменимости.