термех 1 аттестация теории

(P , P ,..., P )

1 2 n

сил (F1, F2 ,..., Fn ),

Основные понятия статики. Аксиомы статики.

Статика изучает методы преобразования сил, приложенных к материальной точке или твердому телу, а также условия их равновесия.

Основные понятия статики Сила - мера механического взаимодействия

материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться.

F =Fxi +Fy j +Fz k

Система сил – совокупность сил, действующих на рассматриваемое тело.

Если линии действия всех сил системы лежат на одной плоскости, то данная система сил называется плоской, а если линии действия которых не лежат на одной плоскости –

пространственной.

Если линии действия всех сил системы пересекаются в одной точке, то данная система сил называется сходящейся, а если линии действия которых параллельны друг другу –

параллельной.

Если одну систему

действующих на свободное твердое тело, можно

заменить другой системой (P , P ,..., P ), не

1 2 n

изменяя при этом состояние покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными: (F1, F2 ,..., Fn )~

Эквивалентной нулю системы сил называется

уравновешенной: (F1, F2 ,..., Fn )~ 0

Если данная система сил эквивалента одной силе

R , то эта сила называется равнодействующей.

(F1, F2 ,..., Fn )~ R

Сила R ′, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется

уравновешивающей силой.

R′= R, (R′, R ) ~ 0

Внешними называются силы, которые действуют на тело (или тела системы) со стороны других тел, а внутренними – силы, с которыми части (или тела системы) действуют друг на друга.

Сила, приложенная к телу в какой – нибудь одной точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

Аксиомы статики:

Аксиомы о силах Аксиома 1 (аксиома об абсолютно твердом теле).

Твердое тело под действием двух сил находится в равновесии только тогда, когда они равны по величине, направлены в противоположные стороны и действуют по одной прямой.

F1 = F2

Аксиома 2 (аксиома о параллелограмме сил). Равнодействующая двух сил, приложенных в одной точке под углом друг к другу, определяется диагональю параллелограмма, построенного на этих силах, как на сторонах.

R = F1 +F2 R =(F1 +F2 )+F3

Аксиомы о связях

Физические условия, ограничивающие свободу движения материальной точки или тела, называется связями.

Сила, с которой связь действует на рассматриваемую материальную точку или тело,

называется реакцией связи.

Аксиома 3 (аксиома об освобождении от связей). Не изменяя движение или равновесие точки, систем или твердого тела, можно отбросить наложенные на них связи, заменив их действия реакциями связи.

Аксиома 4 (аксиома о наложении новых связей). Равновесие системы или тела не нарушится при наложении на них новых связей.

Аксиома 5 (аксиома о затвердении). Если деформируемое тело находится в равновесии, то это равновесие не нарушится, если тело превратится в абсолютно твердое, т.е. затвердеет.

Теорема о переносе силы по линии ее действия. Теорема о трех силах. Теорема о равнодействующей силе

системы сходящихся сил.

Теорема о переносе силы по линии ее действия

Теорема.Силу, приложенную к абсолютно твердому телу, можно перенести по линии ее действия в любую точку.

Доказательство

Теорема о трех силах

Теорема. Если три непараллельные силы, действующие на абсолютно твердое тело, находятся в равновесии и лежат на одной плоскости, то линии их действия пересекаются в одной точке.

Доказательство

Теорема о равнодействующей силе системы сходящихся сил

Теорема. Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна векторной сумме этих сил и проходит через точку пересечения их линий действия.

Доказательство

(F1, F2 )~ R2 , R2 = F1 + F2

(R1, F3 )~ R3 ,

R3 = R2 + F3 = F1 + F2 + F3

(Rn 1, Fn )~ R ,

n

R = Rn 1 +Fn = F1 + F2 +...+Fn =∑Fi

i=1

F1 + F2 = R2

R2 + F3 = R3

R3 + F4 = R

R = F1 + F2 +F3 +F4

n

∑ i

R =

F

i=1

n

R

x

=

F =F

+F

+F

+...+F

∑ ix

1x

2 x

3x

nx

i=1

n

R

y

=

F =F

+F

+F

+...+F

∑ iy

1y

2 y

3 y

ny

i=1

n

R

=

F =F

+F

+F

+...+F

z

∑ iz

1z

2 z

3z

nz

•

i=1

•

R == R2

+R2 +R2

x

y

z

Rx

Ry

Rz

cos R,

i

=

, cos

R, j =

, cos R, k

=

.

R

R

R

n

R

x

=

F =F

+F

+F

+...+F

∑ ix

1x

2 x

3x

nx

i=1

n

R

y

=

F =F

+F

+F

+...+F

∑ iy

1y

2 y

3 y

ny

i=1

R == Rx2 +Ry2

cos R, i = RRx , cos R, j = RRy .

Момент силы относительно точки.

Теорема о моменте ровнодействующей системы сходящих сил(теорема Вариньона).

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на силу.

M0 (F )=r ×F.

M 0 (F )=r * F *sin α = F * h.

Размерность момента силы в системе СИ:

ньютон-метр (НМ).

M0 (F )=2S.

i

j k

o (

)=r ×

=

x y z

=

M

F

F

Fx Fy Fz

=(yFz

zFy )i +(zFx

)j +(xFy yFx

xFz

)k

.

(

)= yFz - zFy ,

M ox

F

(

)= zFx - xFz ,

M oy

F

(

)= xFy - yFx .

M oz

F

Если сила и точкаА лежат на плоскости Oxy, то имеем

Moz (F )= xFy - yFx .

Теорема о моменте равнодействующей системы сходящихся сил (теорема Вариньона)

Теорема. Момент равнодействующей системы сходящихся сил относительно произвольной точки равен векторной сумме моментов составляющих сил относительно этой точки, т.е.:

M o (R )=∑n M o (Fi ).

i=1

Доказательство

Mo (R )= r ×R = r ×(F1 +F2 +...+Fn ) =

=r ×F1 +r ×F2 +...+r ×Fn =

=M o (F1 )+M o (F2 )+...+M o (Fn )=

=∑n M o (Fi ). i=1

Момент силы относительно оси. Главный

вектор и главный момент сил.

Моментом силы относительно оси называется проекция на эту ось момента силы относительно произвольной точки на оси.

M z (F )=Mo cos α.

Moz (F )= xFy - yFx .

MOz (F )= Mo (Fxy )=±Fxy * h.

Момент силы относительно оси равен нулю, если: сила параллельна оси, т.е. проекция силы на плоскость, перпендикулярную оси, равна нулю линия действия силы пересекает ось, т.е. плечо равно нулю.

Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

Главный вектор и главный момент системы сил

Главным вектором системы сил

F1, F2 ,..., Fn называется векторная сумма этих сил, т.е.

n

∑ i

R =

F

i=1

n

n

n

R = F ,

R

y

= F ,

R = F

x

∑ ix

∑ iy

z

∑ iz

i=1

i=1

i=1

R = R2

+R2 +R2 .

x

y

z

Rx

Ry

Rz

cos(i , R ) =

, cos( j, R ) =

,

cos(k , R ) =

.

R

R

R

Главным моментом

системы сил

F1, F2 ,..., Fn

относительно точки называется

векторная сумма моментов этих сил относительно этой точки, т.е.:

n

o =∑

o

(

).

M

M

Fi

i=1

n

n

M ox =∑M Ox

(

), M oy =∑M Oy

(

),

Fi

Fi

i=1

i=1

n

M oz =∑M Oz

(

).

Fi

i=1

n

M ox =∑(yi Fzi - zi Fyi

)

i=1

n

M oy =∑(zi Fxi - xi Fzi

)

i=1

n

M oz =∑(xi Fyi - yi Fxi

)

i=1

R MO = R Mo cos(R, Mo ).

cos(R, M ) = R MO = Rx MOx +Ry MOy +Rz MOz .
o	R Mo	R Mo

Пара сил. Теорема о переносе силы.

Основная теория статики(теорема Пуансо):

Парой сил называется система двух параллельных сил, равных по величине, направленных в противоположные стороны и приложенных к твердому телу.

F ′=-F.

R = F +F ′= F +(- F )=0.

M = F * h.

Теорема. Момент пары сил не зависит от положения точки, относительно которой берется момент.

Доказательство:

Mo (F , F ′) = M o (F )+M o (F ′)=

=M o (F )+M o ( F )=

=O A ×F +O B ×( F )=

=(O A O B )×F = BA ×F .

Теорема о параллельном переносе силы

Теорема. Действие силы на твердое тело не изменится, если перенести ее параллельно самой себе в некоторую точку (центр приведения), присоединив при этом пару сил.

Доказательство:

F′=F′=F.

(F , F ′, F ′) = F , т.к.

(F ′, F ′) ~0

С другой стороны:

(F , F ′, F ′) F ′и (F , F ′)

M (F , F ′) = BA×F.

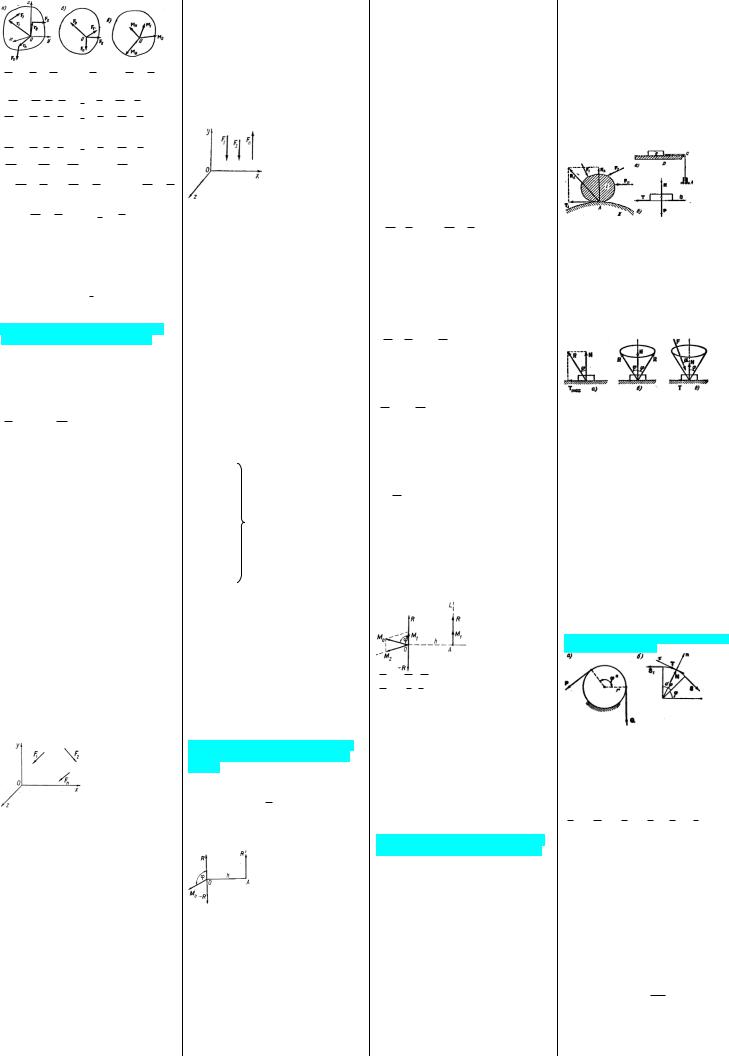
Основная теорема статики (теорема Пуансо)

Теорема. Произвольную пространственную систему сил можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

Доказательство:

n

FO = F1 +F2 +...+Fn =∑Fi = R.

i=1

M1 = M (F1, F1′) =r1 ×F1 = M O (F1 ) M 2 = M (F2 , F2′) =r2 ×F2 = M O (F2 )

M n = M (Fn , Fn′) =rn ×Fn = M O (Fn )

M O = M1 +M 2 +...+M n =

= M O (F1 ) +M O (F2 ) +...+M O (Fn

nn

=∑M O (Fi ) = ∑ri ×Fi .

i=1

i=1

n

∑

i

R =

F .

i=1

n

n

M

O

= M

(F ) = r ×F .

∑ O

i

∑i i

i=1

i=1

Условия равновесия различных систем

сил, приложенных к твердому телу

Условия равновесия пространственной и плоской системы сил.

Условия равновесия произвольной системы сил в пространстве

Произвольная пространственная система сил находится в равновесии, когда главный вектор и главный момент этой системы относительно какой-либо точки в пространстве равны нулю:

R =0, MO =0, где

	n							n
R = F ,				M		O	=	M
	∑ i							∑ iO
	i=1							i=1

n

Rx = ∑Fix = 0, i=1

n

Ry = ∑Fiy = 0, i=1

n

Rz = ∑Fiz = 0 i=1

n

M x = ∑M ix = 0, i=1

n

M y = ∑M iy = 0, i=1

n

M z = ∑M iz = 0 i=1

(Барі бір катарга, еще екеуі жүйе) Произвольная пространственная система сил находится в равновесии, когда алгебраические суммы проекций всех сил на три координатные оси и алгебраические суммы моментов этих сил относительно координатных осей равны нулю.

Условия равновесия сил, произвольно расположенных в одной плоскости

Пусть система сил расположена в плоскости Oxy. Тогда

n

∑Fiz ≡0 i=1

n

∑M ix ≡0 i=1

n

∑M iy ≡0 i=1

Следовательно

n

∑Fix =0 i=1

n

∑Fiy =0

	i=1
n	n
M = M		(F ) =0
∑ iz	∑ O		i
i=1	i=1

Произвольная система сил, расположенных в одной плоскости Oxy, находится в равновесии, когда алгебраические суммы проекций всех сил на две координатные оси (Ox и Oy) и алгебраическая сумма моментов сил относительно произвольной точки этой плоскости равны нулю. Или

n

n

n

F =0,

M

(F ) =0,

M

(F ) =0,

∑ ix

∑ A

i

∑ B

i

i=1

i=1

i=1

где прямая АВ не должна быть перпендикулярной

к оси Ox.

n

n

n

∑ A

∑ B

∑ C

i

i

i

M

(F ) =0,

M

(F ) =

0, M

(F ) =0,

i=1

i=1

i=1

где точки А,В и С не должны лежать на одной

прямой.

Условия равновесия системы

Пусть система сил

параллельна оси

Oy.

Тогда

n

∑ ix

≡0

) =

F

i=1

n

F

≡0

∑ iz

i=1

n

M

≡0

∑ iy

i=1

Следовательно

n

∑Fiy =0 i=1

n

∑M ix =0 i=1

n

∑M iz =0 i=1

Система параллельных сил в пространстве находится в равновесии, когда алгебраические суммы проекций сил на параллельную им ось и алгебраические суммы моментов сил относительно двух других координатных осей равны нулю.

Условия равновесия параллельных сил на плоскости

Пусть силы расположены в одной плоскости Oxyи параллельны, например, оси Оу. Тогда

n
F	≡0
∑ ix
i=1
n
F	≡0
∑ iz
i=1
n
M	≡0
∑ ix
i=1
n
M	≡0
∑ iy
i=1
Следовательно
n		n		n
∑ iy		∑ iz	∑ iO
	F = 0,	M	=	M	= 0
i=1		i=1		i=1

Параллельные силы, расположенные в одной плоскости, находятся в равновесии, когда алгебраические суммы проекций сил на параллельную им ось и алгебраическая сумма моментов этих сил относительно произвольной точки равны нулю.

Или

n		n
M	=0,	M	=0
∑ iA		∑ iB
i=1		i=1

Приведение пространственной систем сил к равнодействующей, к паре сил, к динаме

Приведение пространственной системы сил к равнодействующей. Теорема Вариньона о моменте равнодействующей.

Если главный вектор R и главный момент

M

o

системы сил взаимно перпендикулярны, то

пространственная система сил приводится к

равнодействующей.

′),

~ (

R

,

R

M

O

Где R′=R

h =

M O

R

(R ,

R ) ~0

O

O

(M

, R ) ~

′

O

R

A

Теорема Вариньона о моменте равнодействующей в общем виде Теорема. Если пространственная система сил имеет равнодействующую, то ее момент

относительно некоторой точки равен векторной сумме моментов составляющих сил.

Доказательство

′) =h

′,

M

(R

R

o

A

Где

h =

M o

R′

Следовательно

(

′) =

M o

*

′=

M

R

R

M

o

o

R′

Или

Mo (R′) =Mo

n

Т.к.

M

= M

(F ) ,

o

∑ io

i

i=1

То

n

M

(

R

′)=

M

(F ) ,

o

∑ io

i

i=1

Что требовалось доказать. Следствие.Момент равнодействующей относительно оси равен алгебраической сумме

моментов составляющих сил относительно той же оси

n

M z (R )=∑Miz (Fi )

i=1

Приведение пространственной системы сил к паре сил

Если главный вектор		R =0 , а главный
момент системы сил					не равен нулю, то
	M o

система сил приводится к паре. Момент этой пары равен главному моменту рассматриваемой системы сил:

n

M = M o =∑Mi

i=1

В частности, произвольная система пар сил эквивалентна одной паре сил, момент которой равен геометрической сумме моментов всех пар сил системы (теорема о сложении пар сил):

n

M =∑M i

i=1

Следовательно, произвольная система пар сил уравновешивается, когда векторная сумма моментов пар сил составляющих равна нулю, т.е. когда многоугольник моментов пар сил является замкнутым (условие равновесия системы пар сил):

n

∑M i =0

i=1

Приведение пространственной системы сил к динаме Динамой, или силовым винтом, называется

система, состоящая из силы и пары, момент которой направлен по этой силе.

Если главный вектор и главный момент системы сил не равны нулю и угол между

ними отличен от	, то система сил
приводится к динаме.

M 0 M 1 , M 2

M 2 (R ,-R )

h =

M 2

R

(

0 ,-

0 )~0

R

R

Следовательно

0 ~ (

M

M1, R )

AL – центральная ось системы

M

1

=M

0

cos , где

cos

=

Rx M ox +Ry M oy +Rz M oz

RM 0

Законы трения скольжения. Равновесие тела при наличии трения скольжения.

Основные определения трения.

Трением называется сопротивление, возникающее при перемещении одного тела по поверхности другого.

Если это перемещение представляет собой скольжение, то соответствующее трение называется трением скольжения, или трением первого порядка.

Когда указанное перемещение является качением, то трение называется трением качения,

или трением второго рода.

Первый закон (закон Амонтона - Кулона).

Наибольшая сила трения скольжения пропорциональна нормальной составляющей реакции поверхности связи: Fmax = f * N,

	Fmax	N
где	- наибольшая сила трения,
- нормальная составляющая реакции, f		-
коэффициент трения скольжения.

Второй закон. Трение скольжения зависит от материала и обработки трущихся поверхностей тел.

Третий закон. Трение скольжения не зависит от от скорости и величины поверхности контакта трущихся тел.

Четвертый закон. Сила трения скольжения при движении меньше силы трения при покое. Величина силы трения при движении

определяется по формуле: F			= f	1	* N,
		max
где f	1	- коэффициент трения скольжения при
движении. Опыт показал, что f			< f .

1

Равновесие тела при наличии трения скольжения

		-нормальная сила
N
T		сила трения скольжения
Тогда
N - P =0,			S - T =0.
N - P =0,			S -T =0.

Если тело находится в равновесии, то

T ≤Tmax , где Tmax = fN (закон Амонтона- Кулона)

Тогда T ≤ fN.

	φ = (N , R ) угол трения
	tg =	Tmax				или tgφ = f .
		N
	n
	∑ ix	= T +F sin α =0
	F
	i=1
	n
	∑ iy	= N				F cos α =0
	F

i=1

T =F sin α, N =F cos α

(7.5) :	T ≤ fN
tgα ≤ f ,	f =tgφ

Или α ≤φ Если равнодействующая активных сил находится

внутри конуса трения, то увеличением ее модуля нельзя нарушить равновесие тела.

Для начала движения тела необходимо, чтобы равнодействующая активных сил находилась вне конуса трения.

Трение гибких тел. Равновесие тела тела при наличии трения качения.

Q активная сила			P		сила натяжения троса
Нормальное давление			N		и сила тренияТ

непрерывно распределены по длине охвата φ * r :

N =N(φ ), T =T (φ ) = fN (φ ), r S =S(φ )

Рассмотрим элемент троса длины:

ds =rdφ

На этот элемент троса действуют силы:

Tds, Nds, S и S1 =S +dS

n

dφ

dφ

F

= Nds - S

sin

- S sin

= 0

∑ in

1

2

2

i=1

n

dφ

dφ

F

=Tds +S

cos

- S cos

= 0

1

∑ iτ

2

2

i=1

Т.к. sin

dφ

≈

dφ

, cos

dφ

≈1,

2

2

2

Nds - S1

dφ

dφ

То

2 - S

2 =0

Tds +S1 - S =0

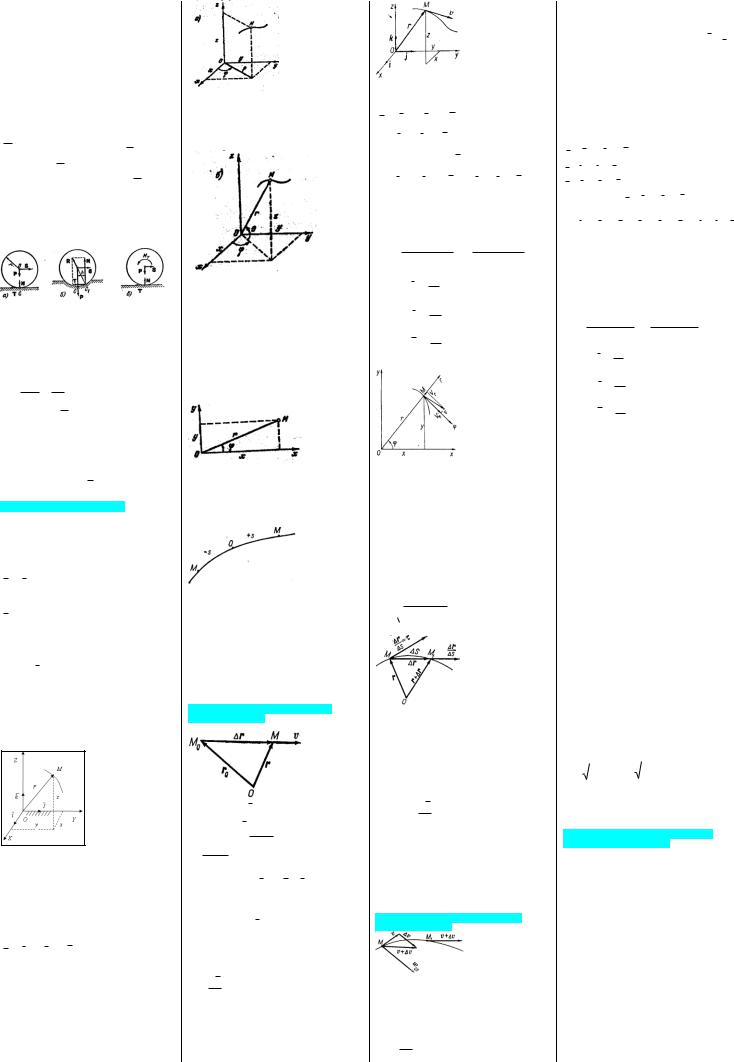
Подставляя (4.15) и (4.16) в (4.19), получим

Nr - S = 0, Tr + dSd = 0,

Откуда S = Nr,

dS =-Trdφ =- fNrdφ =- fSdφ

Или			dS				S	dS
					= - fdφ				= -	fdφ
			S				∫ ∫
						S 0		S		0
		S				,
ln S0 =- f
						где
S0 =Q, S = P,
ln	P		=- f , откуда
	Q
P =Qe- f						-формула Эйлера

Формула Эйлера определяет наименьшую силу

P , способную уравновесить силу Q

Величина силы P , способной преодолеть сопротивление трения вместе с силой Q ,

определяется формулой: P =Qe f

Тогда условие равновесия троса имеет вид:

Qe- f ≤P ≤Qe f .

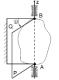
Равновесие тела при наличии трения качения

Mc =-Sr ≠0

MT = Nh - момент трения качения

S - T =0, N - P =0, - Sr +MT =0,

Откуда S =T, N = P, MT =Sr, h = MPT = SrP

С увеличением S растет расстояние hи может нарушиться равновесие

h≤δ,

δ- коэффициент трения качения

MT ≤δN, или S ≤δr N.

Способы задания движения точки

Движение точки можно задать одним из следующих трех способов:

1)векторный;

2)координатный;

3)естественный.

Векторный способ задания движения точки r =r (t) (6,2)

Уравнение (6.2) называется кинематическим уравнениемдвижения точки в векторной форме.

r (t) - является однозначной, непрерывной и

дважды дифференцируемая функция. Геометрическое место концов переменного вектора называется годографом. Следовательно, траектория точки М является годографом радиусвектора r (t)

Координатный способ задания движения точки

Движение точки может быть задано в:

1)декартовых координатах;

2)цилиндрических координатах;

3)сферических координатах;

4)полярных координатах.

Задание движения точки в декартовых координатах

x = x(t)

y = y(t) (6.3)

z = z(t)

Уравнение (6.3) называется кинематическими уравнениямидвижения точки в параметрической форме.

Исключаяиз уравнений (6.3) параметр t, получаем уравнение траектории в явной форме.

Формула, связывающая векторный и координатный способы задания движения точки:

r =i x+ jy+kz

Задание движения точки в цилиндрических координатах

ρ = ρ(t)

φ =φ (t) z = z(t)

ρ-радиус, φ-азимут, z-аппликата

Задание движения точки в сферических координатах

r = r(t)

φ =φ (t) ,

θ = θ(t)

где r - радиус, φ – полюсный угол.

Связь цилиндрических и сферических координат с декартовыми:

x =ρcosφ , y =ρsin φ, z = z

x =r cos θ cos φ, y =r cos θ sin φ, z =r sin θ

Задание движения точки в полярных координатах

r = r(t)

φ =φ (t)

Формулы связывающие полярные координаты с декартовыми:

r =r cos φ, y =r sin φ

Естественный способ задания движения точки

Естественным способом задания движения точки удобно пользоваться, когда траектория точки известна

заранее. s = s(t).(6.9)

Для задания движение точки естественным способом, необходимо знать:

1)траекторию точки;

2)начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета;

3)закон движения точки вдоль траектории в виде

(6.9).

Скорость движения точки в различных системах координат

Скорость движения точки

t0 M0 r0 t1 M1 r1

t =t1 - t0 M0 M 1

где M 0 M 1 - вектор перемещения точки.

OM0 M1 r0 + r =r1

M

M

=

-

=

0

1

r

r

r

1

0

M

0 M

r υ

↑↑

υcp

=

1

=

cp

r

t

t

следовательно

υ =lim( υ

) = lim

r

=

dr

cp

t→0

t

dt

t→0

υ = drdt =r

Вектор скорости точки равен первой производной по времени от радиуса-вектора точки.

Вектор скорости υ направлен по касательной к

траектории точки.

Скорость точки в декартовой системе координат

Пусть движение точки задано координатным способом:

x = x(t), y = y(t), z = z(t)тогда r =i x+ jy+kz

r =i x+ jy+kz

По определению υ =r Тогда

υ =i υx + jυy +kυz =i x+ jy+kz

Следовательно

υx = x, υy =y, υz = z

Проекции скорости на оси декартовой системы координат равны первым производным по времени от соответствующих координат точки.

υ = υ2x +υ2y +υ2z = x2 + y2 +z2 cos(υ, i ) = υυx

cos(υ, j) = υυy cos(υ, k ) = υυz

Скорость точки в полярных координатах

Пусть движение точки в плоскости Оху задано в полярныхкоодинатах:

r =r(t), φ =φ (t) тогда x =r cos y =r sin

υ	x	= x =r cos φ - r sin φ = υ	r	cos φ - υ	sin φ
υ	y	= y = r sin φ+r cos φ = υ	r	sin φ+υ	cos φ

υr =r - проекция скорости на радиальное направление r

υ=r - проекция скорости на

трансверсальное направление

υ = r2 +r2 2

Скорость точки в естественных координатах

Пусть движение точки

задано естественным способом:

s = s(t)

или

υ =r = lim

r

t

t →0

s

υ = lim

r

* lim

=

dr

* s

s→0

s

s→0

t ds

Обозначим drds = τ,

где τ - единичный вектор, направленный по

касательной к траектории. Тогда υ = τs

υ - τ = τ - τs υτ = s

Проекция вектора скорости на направление орта касательной равна первой производной по времени от дуговой координаты.

Ускорения движения точки в различных системах координат

Физическая величина, характеризующая быстроту изменения во времени скорости движения точки, называется ускорением.

M υ

M1 υ+ υ

acp = υt

a = lim a = lim					υ	=	dυ
t→0	ср	t→0			t		dt
Следовательно			dυ				или			d 2r
		a =	dt		= υ				a =	dt 2	=r

Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиусвектора точки по времени.

Ускорение точки в декартовой системе координат

Пусть движение точки задано координатным способом:

x = x(t), y = y(t), z = z(t) тогда r =i x+ jy+kz

r =i x+ jy+kz Продифференцируем r =i x+ jy+kz

По определению r =i x+ jy+kz

Тогда

a =i ax + jay +kaz =i υx + jυy +kυz =i x+ jy+kz

Следовательно

ax =υx = x, ay =υy = y, az =υz = z

Проекции ускорения на оси декартовой системы координат равны первым производным по времени от соответствующих проекций скорости на те же оси или вторым производным по времени от соответствующих координат движущейся точки.

a = ax2 +ay2 +az2 = x2 + y2 +z2 cos(a, i ) = aax

cos(a, j) = aay cos(a, k ) = aaz

Ускорение точки в полярных координатах

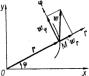Пусть движение точки М в плоскости Оху задано в полярных координатах:

r =r(t),φ =φ (t) тогда x = r cosφ Из рис. видно, что y = r sin φ

ax = ar cos φ - a sin φ ay = ar sin φ +a cos φ

С другой стороны

ax = x = d (r cos φ - r sin φ)/ dt = r cos φ - r sin φ -

-r sin φ - r sin φ - r 2 cos φ = r cos φ - 2r sin φ -

-r sin φ - r 2 cos φ

ay = y = d (r sin φ + r cos φ)/ dt = r sin φ + r cos φ +

+r cos φ + r cos φ - r 2 sin φ = r sin φ + 2r cos φ +

+r cos φ - r 2 sin φ

тогда ar = r - r 2

a = 2r +r

			2		2			2 2			2
								)			+r )
a = ar +a = (r - r									+(2r
tgθ =	a			=	2r +r
	a				r - r 2
			r

Теорема о разложении ускорения по осям естественного трехгранника

Теорема. Полное ускорение точки равно векторной сумме касательного (тангенциального) и нормального (центростремительного) ускорений.

Доказательство. Пусть движение точки задано естественным способом, т.е. s =s(t)

Рассмотрим два бесконечно близких положений точки М на траектории.

t M υ

t1 =t + t M1	тогда
υ1 = υ+ υ

движение будет ускоренным, если

	a = lim	υ	= lim	υ1 - υ
		t		t
	t →0		t →0

Оси естественного трехгранника: Mτ- касательная, Mn - главная нормаль, Mb - бинормаль.

an = lim υ1n -tυn ,

t →0

a = lim

υ1τ

- υτ

,

τ

t →0

t

a =0, где

b

А) υτ = υ и υn =0

Б)

υ1τ = υ1 * cos Δφ

и

υ1n =υ1 *sin φ

тогда

aτ

= lim

υ1 cos

- υ

,

t

t →0

И

an = lim

υ1 sin Δφ

t

t →0

При

t → 0 : φ → 0, s → 0, υ1 → υ

Учитывая lim (cos Δφ) =1, получим:

→0

aτ

= lim

υ1 - υ

= lim

Δυ

=

dυ

t

t

dt

t→0

t→0

a

= lim

υ *

sin Δφ

*

Δφ -

s

=

где

n

t→0

1

t

Δφ*

s

= lim

υ *

sin Δφ

*

Δφ

*

s

t→0

1

Δφ

s

t

lim υ1 =υ,

lim

sin Δφ

=1,

t→0

→0

Δφ

lim

s

= υ,

lim

Δφ

= K =

1

t→0

t

s →0

s

ρ

Тогда

an

=

υ2

ρ

Вектор ускорения равен векторной сумме тангенциального ускорения и нормального ускорения:

a =an +aτ

Тангенциальное ускорение	равно первой
	aτ

производной скорости по времени или второй производной по времени от дуговой координаты:

a		=	dυ	=	d 2 s	Тангенциальное ускорение
	τ		dt		dt 2

характеризует изменение скорости по времени. Нормальное ускорение равно отношению квадрата скорости к радиусу кривизны и оно направлено по главной нормали в сторону вогнутости траектории (к центру кривизны).

aτ = τ * aτ = τ * s an =n * an

=n *

s2

ρ

a =

a2

+a2

aτ

τ

n tgα =

an

ρ =

x2 + y2 + z2

т.к. ρ =

υ2

,

x2 + y2 + z2 - υ2

an

υ2 = x2 + y2 +z2

an = a2 - aτ2 = x2 + y 2 +z 2 - υ2

Частичные случаи движения точки

Прямолинейное движение

Если во время движения an =0 и aτ ≠0, то движение точки является прямолинейным.

Если an	=0 то υ2			откуда ρ =∞
		ρ	=0,

a =aτ

Равномерное прямолинейное движение

Если во время движения an =0 и aτ =0, то

движение точки является равномерно прямолинейным.

Скорость точки в этом случае не изменяется ни по величине, ни по направлению.

Равномерное криволинейное движение

Если во время движения						an ≠0	и	aτ =0,
то движение точки является равномерно
криволинейным.
Так как	aτ =0,				то υ =const.
a =an	=	υ2		ds	= υ
				dt
		ρ

ds =υdt

ds = υdt s =υt +c1
∫ ∫
При	t =0 : s =s0 , c1 =s0
Тогда		s = s0 +υ * t

Равнопеременное криволинейное движение

Если во время движения точки по кривой

aτ =const,			то движение точки является
равнопеременно криволинейным.
Если	τaτ ↑↑υ		равноускоренное движение
Если	τaτ	↑↓υ		равнозамедленное движение

ddtυ = aτ ∫dυ = ∫aτ dt,

υ =aτt +c1

При t =0 : υ =υ0 , c1 =υ0 Тогда υ =υ0 +aτt

dsdt = υ0 +aτ * t ds =υ0dt +aτ *tdt

s = υ0t +aτ t 2 +c2

2

При t =0 : s =s0 , c1 =s0 тогда s =s0 +υ0t +aτt 2 / 2 Если при

криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.

Так как изменение модуля скорости характеризуется касательным ускорением, то

υ и aτ

имеют одинаковые знаки, т.е. угол между

υ и aτ	острый и наоборот.

Прямолинейное гармоническое колебание

x =a cos kt

где a - амплитуда, k - круговая частота, kt - фаза колебания

T = 2kπ -период колебания

υ =υx =-ak sin kt

a =ax =-ak 2 cos kt

Поступательное движение твердого тела. Угловая скорость и угловое ускорение тела, вращающегося вокруг неподвижной оси

Поступательное движение твердого тела

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная на этом теле, перемещается, оставаясь параллельной самой себе.

AB =CD и AB || CD

AD = BC и AD || BC

Теорема 1.При поступательном движении твердого тела его точки описывают одинаковые траектории.

Доказательство.

rM =rA +r, где r = AM =const

Теорема 2.При поступательном движении твердого тела в каждый момент времени все его точки имеют равные скорости и ускорения.

Доказательство.

rM =rA +r т.к.

r =const, то r =0 следовательно

υM = υA , υM = υA или aM =aA Изучение поступательного движения твердого

тела сводится к изучению движения одной точки тела, т.е. сводится к задаче кинематики точки. Уравнения поступательного движения тела:

xA = xA (t), yA = yA (t), zA =zA (t)

Вращательное движение твердого тела вокруг неподвижной оси

Вращательным движением твердого тела вокруг неподвижной оси называется такое движение, при котором прямая, проходящая через две

точки, остается неподвижной во время движения тела. Эта прямая называется осью вращения тела.

Кинематическое уравнение вращательного движения тела вокруг неподвижной оси:

υ=υ (t)

υ=2πN

Угловая скорость тела, вращающегося вокруг

неподвижной оси

t =t1 - t, Δυ=υ1 - υ

ωср = υt

	ω = lim (ω		) = lim	ω	=	dω	=φ
		ср
	t→0		t→0	t dt

[рад/с] или [1/с]

Угловая скорость тела в данный момент времени характеризует скорость изменения во времени угла поворота тела и равна первой производной по времени от угла поворота.

ω = 260nN = 30πn Если ω=const то вращение тела называется равномерным. ddtυ = ωt dυ =ωdt

∫dυ = ∫ωdt υ =ωt +c1 при

t =0 : υ =υ 0 , ω =0 c1 =υ 0

Следовательно, уравнение равномерного вращения тела вокруг неподвижной оси:

φ =φ0 +ωt

Угловая скорость является скользящим вектором

ω , направленным по оси вращения.

Угловое ускорение тела, вращающегося вокруг неподвижной оси

Угловое ускорение тела характеризует скорость изменения угловой скорости во времени.

	t =t - t1, Δω=ω - ω1 εср							=	Δω
									t
	ε = lim ε		= lim	Δω	=	dω	= ω =υ "
		ср
	t →0		t →0 t			dt

Угловое ускорение является скользящим вектором, направленным по оси вращения тела.

Если ε ↑↑ω, то вращение тела называется

ускоренным.

Если ε ↑↓ω, то вращение тела называется

замедленным.

Если ε =0, ω =const, то вращение тела

называется равномерным.

Если ε =const ≠0, то вращение тела называется равнопеременным.

Скорость и ускорениет точек, вращающегося вокрук неподвижной оси Скорости точек тела, вращающегося вокруг неподвижной оси

Скорость любой точки тела, вращающегося вокруг неподвижной оси,

называется линейной или окружной скоростью.

s = s(t) Пусть за элементарное время dt точка

M совершает элементарное перемещение ds=Rdφ

Тогда υ = dsdt = R ddtφ = Rω или υ =s = R

Линейная скорость точки тела, вращающегося вокруг неподвижной оси, по величине равна произведению радиуса вращения на величину угловой скорости.

Теорема Эйлера.Вектор линейной скорости точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению угловой скорости на радиус-вектор точки: υ =ω×r

Доказательство

R =r sin(ω, r )

υ =ω R =ω * r sin(ω, r ) Тогда из определения

о векторном произведении двух векторов ω и r получаем υ =ω×r

		i	j	k	i (ωy rz - ωz ry ) + j(ωz rx - ωx rz ) +
	=	ωx	ωy	ωz	=+k (ωx ry - ωy rx ),
υ
		rx	ry	rz

Где rx = x, ry = y, rz = z,

ωx =0, ωy =0, ωz =ω.

υx = ω y

Тогда υ y =ωx

υz =0

Ускорения точек тела, вращающегося вокруг неподвижной оси

Согласно теореме о разложении ускорения имеем:

a =an +aτ , где

an

=

υ2

=

υ2

,

aτ

=

dυ

ρ

R

dt

Тогда a

=

υ2

=

(ω R)2

= Rω2 ,

n

ρ

R

aτ

=

dυ

=

d (ω R)

= R

dω

=ε R

dt

dt

dt

Нормальное ускорение точки тела при вращении его вокруг неподвижной оси равно произведению радиуса вращения на квадрат угловой скорости. Касательное ускорение равно произведению радиуса вращения на угловое ускорение.

a = an2 +aτ2 = R2ω4 +R2ε2 = Rω4 +ε2

tgα =	aτ		=	ε R	=	ε
				ω2 R		ω2
	a	n

Скорость и ускорение точек тела при плоскопаралеьном движении

Плоско-параллельным или плоским движением твердого тела называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Теорема.Перемещение плоской фигуры в ее плоскости можно осуществить путем поступательного перемещения вместе с полюсом и вращения вокруг полюса. При этом угол поворота не зависит от выбора полюса.

Доказательство

B1 A2 = AB

B A || AB или A B′= AB , A B′|| AB
1	2	1	2	1	2

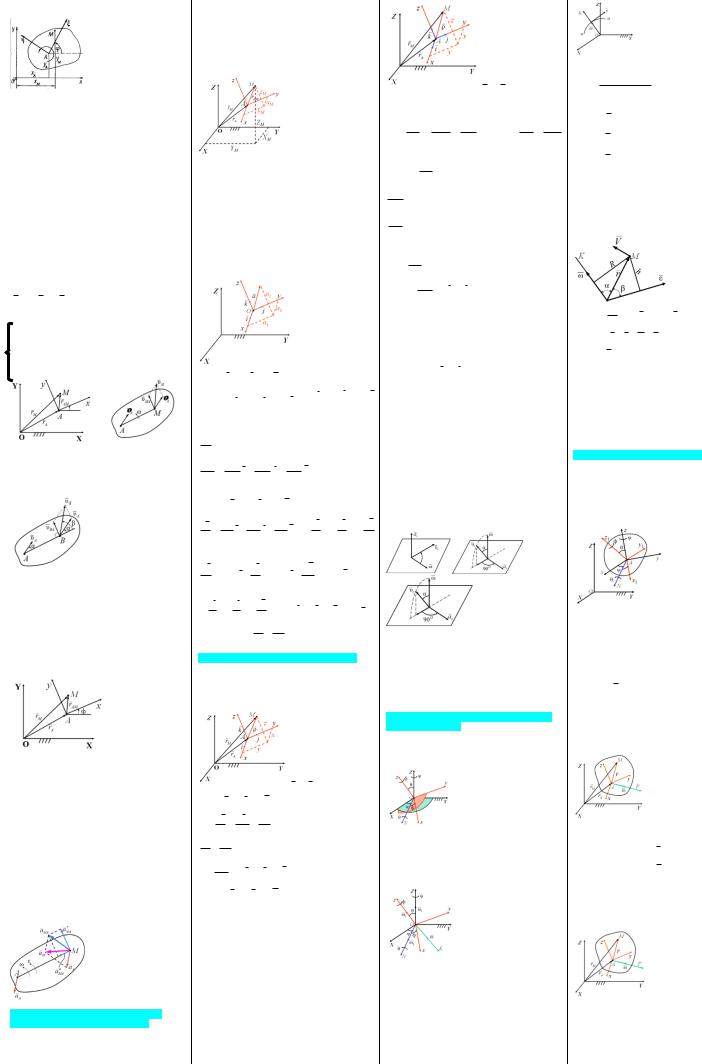
Кинематические уравнения плоскопараллельного движения

xA = xA (t)

yA = y A (t)

υ=υ (t)

xM = xA +ξ cos υ - η sin φ yM = yA +ξ sin υ +η cos φ

	xM	=	xA	+	cos φ	- sin φ	*	ξ
	yM		yA		sin φ	cos φ		η
	[R]=	cos φ		- sin φ		матрица вращения
		sin φ		cos φ

подвижной системы координатА

Скорость точек тела при плоско-параллельном движении Теорема. При плоско-параллельном движении

твердого тела скорость любой ее точки равна векторной сумме скорости полюса и скорости точки во вращательном движении вокруг полюса.

Доказательство rM =rA +rAM

υM = υA +υMA где

υMA =			×		AM
				r
υ	MA	=ω		AM жуйе

υM = υA +υMA

Теорема о проекциях скоростей двух точек тела Теорема.Проекции скоростей двух точек

твердого тела на ось, проходящую через эти точки, равны друг другу.

Доказательство

υB = υA +υBA где

υBA AB тогда υB cos β =υA cos α

Ускорения точек при плоско-параллельном движении Теорема. Ускорение любой точки тела при

плоско-параллельном движении равно векторной сумме ускорения полюса, вращательного (тангенциального) и центростремительного (нормального) ускорений.

Доказательство

rM =rA +rAM

d 2

d 2

d 2

r

r

r

M

=

A

+

AM

dt 2

dt 2

dt 2

Или aM =aA +aMA

где aMA =aMAτ +aMAn

тогда aM =aA +aMAτ +aMAn aMAn =ω2 * AM

aMAτ =ε * AM aMA =aMAn +aMAτ aM =aMA +aA

Сложное движение точки. Абсолютная и относительная производные вектора.

Сложное движение точки

Движение точки M относительно абсолютной системы координат OXYZ называется

абсолютным.

Движение точки M относительно подвижной системы координат Axyz называется

относительным.

Движение, совершаемое подвижной системы координат Axyz по отношению к абсолютной системе координат OXYZ, является для точки

Mпереносным движением.

Уравнения абсолютного движения точки M:

X M = X M (t) YM =YM (t) ZM = ZM (t)

Уравнения относительного движения точки M: xM = xM (t)

yM = yM (t) zM = zM (t)

Абсолютная и относительная производные вектора

a =axi +ay j +az k

da

=

dax

i +

da y

j +

daz

k +a

di

+a

dj

+a

dk

dt

dt

dt

dt

x

dt

y

dt

z

dt

Обозначим:

da - абсолютная производная вектора a

dt

ddt′a = dadtx i + dadty j + dadtz k - относительная производная вектора a

a =axi +ay j +az k

dadt = dadtx i + dadty j + dadtz k +ax didt +ay dtdj +az dkdt

Согласно формуле Эйлера:

didt =ω ×i , dtdj =ω × j, dkdt =ω ×k

Тогда

ax didt +ay dtdj +az dkdt = ω×(axi +ay j +az k ) = ω×a

Следовательно ddta = ddt′a +ω×a

Теорема о сложении скоростей и ускорении

Теорема о сложении скоростей Теорема. Абсолютная скорость точки равна

векторной суммевввввввввввв переносной и относительной скоростей.

r =rA +ρ где

ρ = xi + yj +zk

υ = drdt = drdtA + ddtρ ddtρ = ddt′ρ +ω×ρ

Где ddt′ρ = xi + yj + zk или

υr = xi + yj +zk

Тогда υ = υA +ω×ρ +υr , где

υe = υA +ω×ρ

Следовательно υ = υe +υr

Теорема о сложении ускорений Теорема. Абсолютное ускорение точки равно

векторной сумме переносного, относительного и кориолисова ускорений.

Доказательство

r =rA +ρ

υ = υA +ω×ρ +υr

a = ddtυ = ddtυA + ddtω ×ρ +ω×ddtρ + ddtυr

где a = ddtυ -абс. ускорение точки

ddtυA =aA - ускорение точкиА

ddtω = ε - угловое ускорение подв. системы координат Axyz

dρ

=

d′ρ +ω×ρ где

υr =

d ′ρ - относительная

dt

dt

dt

скорость

d′ρ = xi + yj

+zk

dt

dυ

r

d′υ

где

=

r

+ω×υ

r

dt

dt

d ′υ

=a - относительное ускорение

r

dt

r

d

′υ

a

=

r

= xi + yj +zk

r

dt

Тогда

a =aA +ε ×ρ +ω×[υr +(ω×ρ)]+(ar +ω×υr ) =

=aA +ε ×ρ +ω×(ω×ρ)+ar +2ω×υr ,

Где a =a

A

+ε×ρ +ω×(ω×ρ) -

e

переносное ускорение

Следовательно a =a +a +2ω×υ

, где

e

r

r

a =2 * ω×υ

- поворотное (кориолисово)

c

r

ускорение

Окончательно получим

a =ae +ar +aс

где

ac =2ω * υr

sin(ω, υr )

Кориолисово ускорение равно нулю в следующих случаях:

1) при ω =0 , это будет при поступательном перемещении подвижной системы координат;

2) когда ω параллельна υr ;

3) когда υr =0 .

Вращение твердого тела вокруг неподвижной точки. Углы Эйлера.

Движение твердого тела, при котором одна точка в теле все время остается неподвижной, называется вращательным движением твердого тела вокруг неподвижной точки.

ON - линия узлов (линия пересечения плоскостей OXYZ и Oxyz)

Ψ - угол прецессии Φ - угол собственного вращения θ - угол нутации

Кинематические уравнения вращения твердого тела вокруг неподвижной точки

	ψ = ψ(t)
		ω = ψ +θ +φ =
	θ =θ(t)	= ω1	+ω2		+ω3
	φ =φ (t)

ε = ω

εx =ωx , ε y =ωy , εz =ωz ,

ε = ε2x +ε2y +ε2z

cos(ε, X ) =ε x / ε cos(ε, Y ) =ε y / ε cos(ε, Z ) =ε z / ε

Ускорения точек тела, вращающегося вокруг неподвижной точки Теорема. Ускорение любой точки тела,

вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного ускорений.

Доказательство

a= υ = dtd (ω×r ) = ω×r +ω×r =

=ε ×r +ω×υ

Где ε×r =a вр , ω×υ =a ос Следовательно

a =a вр +a ос

aвр =ε * r *sin β =εh

aос =ω* υ *sin α =ωυ =ω2 R

Свободное движение твердого тела

Кинематические уравнения движения свободного твердого тела

Движение свободного твердого тела в пространстве можно представить состоящим из поступательного движения тела вместе с полюсом и мгновенно вращательного движения тела вокруг полюса.

xA = xA (t), yA = yA (t), zA = zA (t)

ψ = ψ(t), θ =θ(t), φ = φ(t)

υAx = xA ,		υAy = yA , υAz = zA
aAx = xA ,		aAy = yA , aAz = zA
ω = ψ +θ +φ ;			ε = ψ +θ +φ

Скорости точек свободного твердого тела Теорема. Скорость любой точки свободного твердого тела равна векторной сумме скорости полюса и скорости во вращательном движении тела вокруг полюса.

Доказательство

υ = υe +υr , где

υe = υA , υr =ω×r

Тогда υ = υA +ω ×r

Ускорения точек свободного твердого тела Теорема. Ускорение любой точки свободного твердого тела равно векторной сумме ускорений полюса, вращательного и осестремительного ускорений.

Доказательство

a =ae +ar +aс

Где ae =aA , ac =0, ar =arвр +arос

Тогда a =aA +arвр +arос

- количество движения

Где arвр =ε×r, arос =ω×r

Введение в динамику. Законы Ньютона

Динамикой называется часть теоретической механики, в которой изучается механическое движение материальной точки, системы материальных точек, абсолютно твердого тела с учетом действующих сил.

Разделы динамики:

1.Динамика материальной точки

2.Динамика системы материальных точек

3.Динамика абсолютно твердого тела

Первый закон Ньютона

Изолированная материальная точка движется равномерно и прямолинейно, либо находится в покое до тех пор, пока действие других тел на эту материальную точку не изменит это состояние.

Изолированной называется материальная точка, взаимодействием которой с окружающими телами пренебрегают.

Мерой взаимодействия материальной точки с другими телами являются механические силы.

Второй закон Ньютона (основной закон динамики)

Скорость изменения количества движения материальной точки равна силе, действующей на эту точку

d(dtmυ)= F , где mυ

материальной точки.

Принимая m =const , получим

ma = F

Действующая на материальную точку сила равна произведению массы точки на ее ускорение.

m =		m0				,
	1 -		υ 2
			c

где m0 – масса покоящегося тела; 300000 км/с – скор.света.

Третий закон Ньютона

Силы взаимодействия двух материальных точек равны по величине, направлены в противоположные стороны и имеют общую линию действия.

Если первый и второй законы Ньютона относятся к динамике материальной точки, то третий закон относится к динамике системы материальных точек.

Закон независимости действия сил (принцип суперпозиции)

Ускорение материальной точки, возникающее при одновременном действии на нее нескольких сил, равно векторной сумме ускорений, сообщаемых точке отдельными силами.

Пусть силы F1, F2 ,..., Fn сообщают материальной точке ускорения a1, a2 ,..., an .

Тогда	a =a1 +a2 +...+an (*m)

ma =ma1 +ma2 +...+man

Или ma = F1 +F2 +...+Fn =∑Fi

Таким образом, движение материальной точки под действием сил F1, F2 ,..., Fn будет таким

же, как и при действии одной силы, равной их векторной сумме (равнодействующей).

Дифференциальные уравнения движения точки. Два основные задачи динамики.

Динамические дифференциальные уравнения движения материальной точки

Основное уравнение динамики:

mr = F (1) или

mx = Fx (t, x, y, z, x, y, z) (2) my = Fy (t, x, y, z, x, y, z)

mz = Fz (t, x, y, z, x, y, z)

Уравнения (2) называются динамическими уравнениями движения материальной точки в координатной форме.

	dυ		= Fτ	(t, s, s)
m dt
				(8)
mυ2			= Fn (t, s, s)
ρ

0 = Fb

(8) уравнение называются динамическими уравнениями движения точки в естественной форме.

Две основные задачи динамики свободной материальной точки

Прямая задача динамики

“Определить силу , действующую на материальную точку, если заданы ее масса и кинематические уравнения движения”.

а) Заданы: m и

x = x(t), y = y(t ), z = z(t).

Необходимо определить F .

Решение

ax = x, ay = y, az = z

Fx =mx, Fy =my, Fz =mz

F = X 2 +Y 2 +Z 2

Fx

Fy

Fz

=

; cos (

, j)=

=

cos F ,i

F

; cos F , k

F

F

F

б) Заданы: m и s =s(t).

Необходимо определить F .

Решение

υ =

ds

dt

a

=

dυ

, a

=

υ2

,

a =0

n

τ

dt

ρ

b

Fτ =maτ ; Fn =man ; Fb =0

F = F 2 +F 2 ,

Fτ

τ

n

tgα = Fn

Обратная задачадинамики

“Определить кинематические уравнения движения материальной точки, если заданы ее

масса, главный вектор F , приложенных к ней сил и начальные условия движения”.

а) Заданы:

m, Fx , Fy , Fz ; x = x0 , y = y0 ,

z = z0 ; x = x0 , y = y0 ,				z = z0
Необходимо определить
x = x(t), y = y(t), z = z(t).
Решение:
mx = Fx		(t; x, y, z; x, y, z)		(1)
my = Fy		(t; x, y, z; x, y, z)
mz = Fz		(t; x, y, z; x, y, z)
x = x(t; c1, c2 ,..., c6 )			(2)
y = y(t; c1, c2 ,..., c6 )
z = z(t; c1, c2 ,..., c6 )
x = x(t; c1, c2 ,..., c6 )			(3)
y = y(t; c1, c2 ,..., c6 )
z = z(t; c1, c2 ,..., c6 )

x0 = x(t0 ; c1, c2 ,..., c6 )

y0 = y(t0 ; c1, c2 ,..., c6 ) (4) z0 = z(t0 ; c1 , c2 ,..., c6 )

x0 = x(t0 ; c1, c2 ,..., c6 ) y0 = y(t0 ; c1, c2 ,..., c6 ) z0 = z(t0 ; c1 , c2 ,..., c6 )

ci = ci (t0 ; x0 , y0 , z0 ; x0 , y0 , z0 );

i =1,...,6
x = x(t), y = y(t), z = z(t)
б) Заданы: m, F ,		F ; s =s ,		υ =s
	τ	n	0	0
s =s(t)
Решение mυ = Fτ	(t, s, s)
υ2

m ρ = Fn (t, s, s)

0 = Fb

s = s(t; c1, c2 ) s = s(t; c1, c2 ) s0 = s(t0 ; c1 , c2 ) s0 = s(t0 ; c1 , c2 )

ci =ci (t0 ; s0 , s0 ); (i =1,2) s =s(t)

Этапы решения обратной задачи динамики:

1)Составление динамических уравнений движения материальной точки

2)Интегрирование полученной системы дифференциальных уравнений

3)Определение значений постоянных интегрирования с учетом начальных условий движения

Основные меры механического движения. Теоремы об изменении количества движения и момента количества движения.

Количество движения

Количеством движения материальной точки называется вектор, равной произведению массы точки на ее скорость:

=mi υi

Qi

dK0i

внут

внеш

= M

0i (Fi

)+M

0i (Fi

)

Количеством движения системы материальных

dt

точек называется векторная сумма количеств

движений всех ее точек:

d

n

n

∑K0i

= ∑M 0i (Fi внут )+

n

n

dt

Q =

∑ i

=

∑ i

i

i=1

i=1

Q

m υ

n

i=1

i=1

∑

0i

(

внеш )

M

Fi

Кинетическая энергия

i=1

Кинетической энергией материальной точки

n

называется скалярная величина, равная половине

Где

K

= K

произведения массы точки на квадрат модуля ее

∑

0i

0

скорости:

i=1

1

n

T =

m υ2

∑

0i (

внут )= 0,

M

Fi

i

2

i

i

i=1

Кинетической энергией системы материальных

n

∑

0i

(

внеш )=

0

точек называется сумма кинетических энергий

M

Fi

M

всех ее точек:

i=1

n

n

mi υi2

dK

T =∑Ti =∑

Тогда

0

= M

0

2

i=1

i=1

dt

Момент количества движения

dKOx

= M

Моментом количества движения (или

кинетическим моментом) материальной точки

dt

Ox

относительно центра О называется векторное

dKOy

произведение радиус-вектора материальной

= M Oy

точки на ее количество движения:

dt

KOi

=ri ×mi υi

dKOz

Моментом количества движения относительно

= M

оси называется проекция на эту ось момента

dt

Oz

количества движения материальной точки

относительно любой точки, взятой на оси.

Моментом количества движения (или

кинетическим моментом) системы

Работы силы, мощность. Вычисление работы

материальных точек относительно центра O

внешних сил, приложенных к твердому телу.

называется главный момент количества

Теорема о изменении кинетической энергии.

движения всех ее точек относительно этого

Работа силы, мощность

центра:

При F =const : A=F

s cos α

n

O =∑

K

K

При F ≠const : dA= F

Oi

dr

i=1

Теорема об изменении количества движения

M

A =

∫

Изменение количества движения материальной

F

dr

точки определяется вторым законом Ньютона:

M 0

d (mi υi )

При векторном способе задания движения:

= F

dt

dA= F

dr

Теорема.Первая производная по времени от

При координатном способе задания движения:

количества движения системы материальных

dA= Fx dx+Fy dy+Fz dz

точек равна главному вектору внешних сил.

Доказательство.

При естественном способе задания движения:

d(mi υi )

внеш +

внут

= F

F

i

dA= Fds

dt

cos (F , τ)

d

n

n

внеш +

n

внут

Единица измерения работы: 1 Дж=1Нм=1кГм2 /с2 .

m υ =

F

F

dt

∑ i

i

∑ i

∑ i

N =

dA

=

F ds

= F υ

i=1

i=1

i=1

dt

dt

n

n

Единица измерения мощности: 1 Вт=1Дж/с.

Где ∑m υ =Q

F

внеш

=

R

внеш

Теорема.Работа равнодействующей силы равна

i

i

∑ i

алгебраической сумме работ ее составляющих.

i=1

i=1

Доказательство

n

F

внут

=

R

внут ,

R

внут =0

R = F +F +...+F +...+F

∑ i

1

2

i

n

i=1

внеш dQx

dA = R

dr = (F1 +F2 +...+Fi +...+Fn )

dr = F1 dr +

Тогда

dQ

внеш

...+Fi

dr +...+Fn

dr = dA1 +dA2 +...+dAi +...+dAn

dt

= R

dt

= Rx

,

dQy

внеш

dQ

внеш

Вычисление работы внешних

z

= Ry

,

= Rz .

сил,приложенных к твердому телу

dt

dt

Поступательное движение

При поступательном движении

d(mi υi )= Fi dt

=0 тогда

d

F dt =dS

- элементарный импульс силы

F

dA= R

dr

i

i

c

Следовательно, при поступательном движении

d(mi υi )=dSi

твердого тела элементарная работа внешних сил

υi

ti

равна работе главного вектора этих сил на

(mi

i )=

dt

элементарном перемещении центра масс.

d

υ

Fi

∫

∫

Вращательное движение вокруг неподвижной оси

υ0 i

0

Выбирая полюсО на оси вращения Oz твердого

ti

- импульс силы

Fi

тела, получим:

∫

Fi dt

= Si

0

dr0 =0, M0 * d = M z d

Тогда

mi υi - mi υOi = Si

Тогда

dA=M z d

Теорема об изменении момента количества

Следовательно, во вращательном движении

движения материальной точки

твердого тела вокруг неподвижной оси

Теорема.Первая производная по времени от

элементарная работа внешних сил, приложенных

момента количества движения материальной

к твердому телу, равна работе главного момента

точки равна моменту равнодействующей силы.

этих сил относительно оси вращения на

элементарном угловом перемещении тела.

K0i =ri ×mi υi

Плоско-параллельное движение

d(mi

)

dK0i

dri

υ

i

dA= R drc +Mcz d

=

×mi υi +ri ×

= υi ×mi υi +ri

×Fi

dt

dt

dt

Элементарная работа внешних сил, приложенных

к твердому телу, совершающему плоско-

Где

υi ×mi υi

=0,

ri ×Fi =M0i

параллельное движение, равна сумме работ

главного вектора этих сил на элементарном

Тогда

dK0i

= M 0i

перемещении центра масс тела и главного

dt

момента этих сил относительно центра масс на

dK0i x

= M

,

dK0iy

= M

,

dK0iz

= M

элементарном вращательном движении вокруг

0i x

0iy

0

iz

центра масс.

dt

dt

dt

Теорема об изменении кинетической

энергииматериальной точки

Теорема об изменении момента количества

Теорема.Приращение кинетической энергии

движения системы материальных точек

материальной точки на некотором участке

Теорема.Первая производная момента

траектории равняется работе

количества движениясистемы равна главному

равнодействующей силы на том же участке

моменту внешних сил.

траектории.

Доказательство

Доказательство

d(mυ)

d(mυ)

υ

dr

=

F

= F

dt

dt

dt

m

2

d(m

)=

dr d

υ

F

= F dr

υ

υ

2

dT =dA

Следовательно, элементарное приращение кинетической энергии материальной точки равно элементарной работе приложенной к ней силе

(теорема об изменении кинетической энергии материальной точки в дифференциальной форме).

	T			M
	dT =			dA
	∫ ∫
	T0			M 0
	T - T0 = A
	mυ2		mυ2
		-	0	= A
	2		2

Равенство (26.8) выражает теорему об изменении кинетической энергии материальной точки в интегральной форме.

Теорема об изменении кинетической энергии системы материальных точек Теорема.Приращение кинетической энергии системы материальных точек за некоторый промежуток времени равно сумме работ внешних и внутренних сил, действующих на материальные точки системы в течение рассматриваемого промежутка времени.

Доказательство

mi υi2

mi υi20

= Ai (

внеш )+ Ai (

внут )

-

Fi

Fi

2

2

1 n

2

1

n

2

=

m υ

i

-

m υ

Oi

∑ i

∑ i

2 i=1

2 i=1

n

n

∑Ai (

внеш )+∑Ai

(

внут )

Fi

Fi

i=1

i=1

0

n

=

∑ i

T - T

A

i=1

T =

1

n

m υ2

∑ i

i

2 i=1

T0 = 12 ∑n mi υi20 i=1

∑n Ai =∑n Ai (Fi внеш )+∑n Ai (Fi внут )

i=1

i=1

i=1