
- •Линейная алгебра
- •Основные вопросы программы раздела «линейная алгебра»
- •Решение типовых задач раздела
- •Задачи для самостоятельной и практической работы
- •Рейтиноговая оценка знаний студенТов
- •Список используемой литературы
- •Содержание
- •Н.Б. Панченко, ассистент Редактор: о.М. Барбаков, д.С.Н., профессор
- •625000, Г. Тюмень, ул. Володарского,38
- •625039, Г. Тюмень, ул. Киевская, 52
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Тюменский государственный нефтегазовый университет»
Институт менеджмента и бизнеса
Кафедра «Математические методы в экономике»
Линейная алгебра
и
аналитическая геометрия
Методические указания к практическим и самостоятельным работам
по дисциплинам «Математика»,
«Линейная алгебра», «Алгебра и геометрия»
для студентов всех форм обучения
всех направлений бакалавриата
Часть 1
Тюмень
ТюмГНГУ
2012
Утверждено редакционно-издательским советом
Тюменского государственного нефтегазового университета
Составители: Ю.С. Бердова, ассистент
Н.Б. Панченко, ассистент
Редактор: О.М. Барбаков, д.с.н., профессор
Федеральное государственное бюджетное образовательное учреждение высшего
профессионального образования
«Тюменский государственный нефтегазовый университет», 2012 г.
Введение
Получение высшего образования по всем направлениям бакалавриата требует высокой математической культуры, достаточного глубокого владения рядом специальных математических методов и умения непосредственного их применения в профессиональной деятельности.
Основная цель методических указаний – овладение студентами необходимым математическим аппаратом, помогающим анализировать, моделировать и решать прикладные задачи с применением ЭВМ.
В помощь студенту предлагается подробное решение типовых задач раздела «Линейная алгебра», а также предложены задачи, как для самостоятельного решения, так и для решения на практических занятиях.
Каждый преподаватель может самостоятельно распределить нагрузку на определенное практическое занятие в соответствии с учебным планом, в зависимости от поставленных целей и задач данного занятия. Каждый раздел содержит задачи различной степени сложности, что позволяет дифференцированно подойти к процессу обучения.
Основные вопросы программы раздела «линейная алгебра»
Матрица, основные понятия и обозначения.
Виды матриц.
Сложение матриц.
Умножение матрицы на число.
Произведение матриц.
Определитель матрицы, основные обозначения и формулы.
Теорема Лапласа.
Обратная матрица.
Ранг матрицы.
Система линейных уравнений, основные понятия и определения.
Метод Гаусса, прямой и обратный ход.
Метод обратной матрицы.
Метод Крамера.
Метода Жордана – Гаусса.
Вектор, основные понятия и определения.
Действия над векторами.
Проекция вектора на ось.
Координаты вектора, длина, направляющие косинусы.
Скалярное произведение векторов.
Свойства скалярного произведения.
Векторное произведение векторов.
Свойства векторного произведения.
Смешанное произведение векторов.
Свойства смешанного произведения.
Решение типовых задач раздела
Найти линейные комбинации заданных матриц:
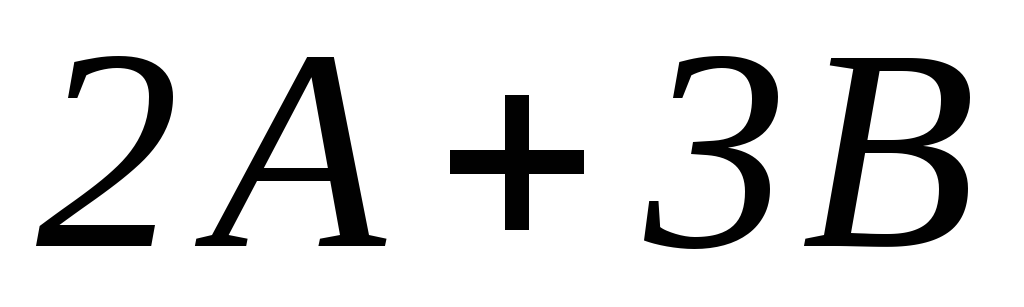 ,
где
,
где
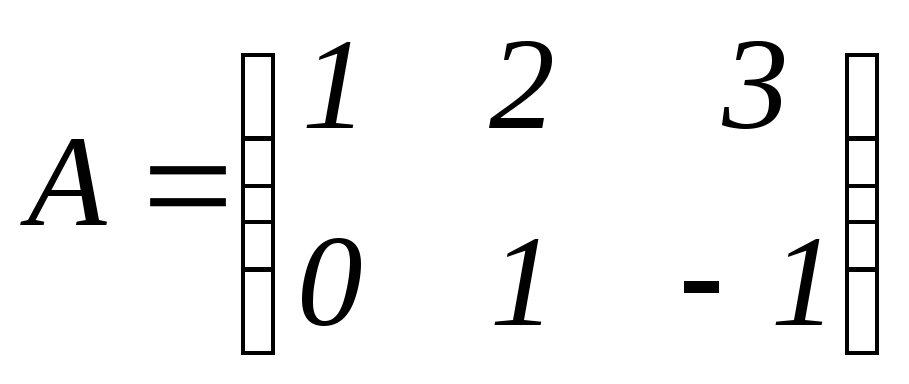 ,
, .
.
Решение.
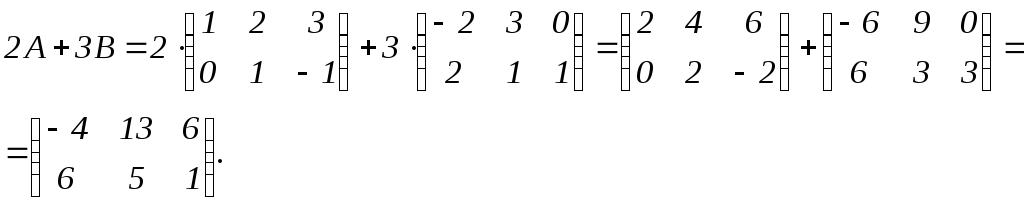
 ,
где
,
где
 .
.
Решение.
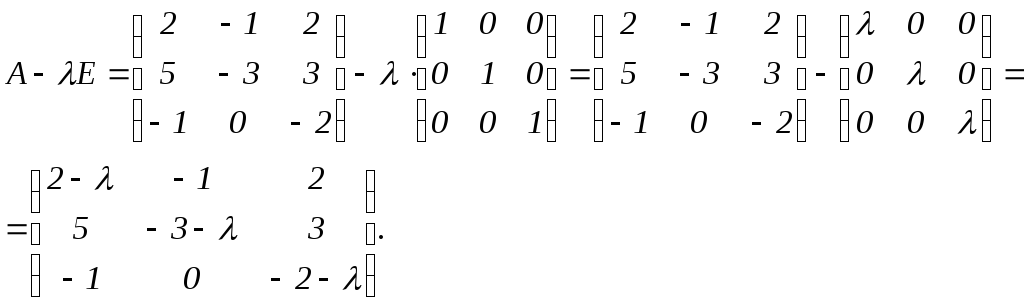
Найти произведение матриц
 и
и ,
если это возможно:
,
если это возможно: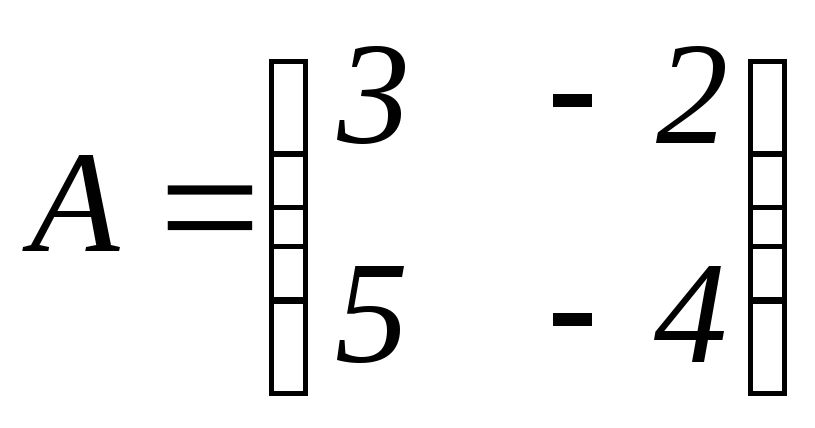 ,
,
 .
.
Решение.
![]()
![]()
Найти значение матричного многочлена
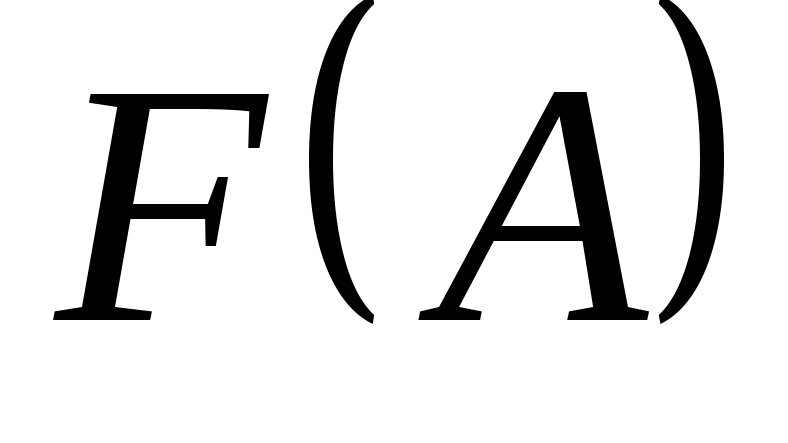 ,
если:
,
если: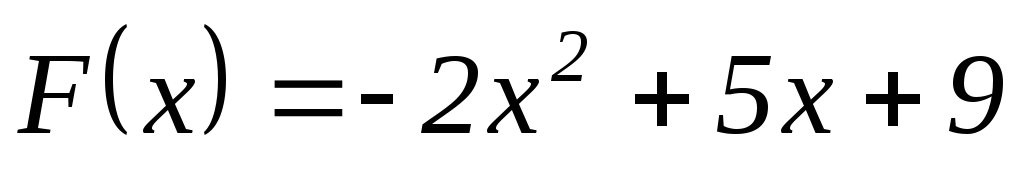 ,
,
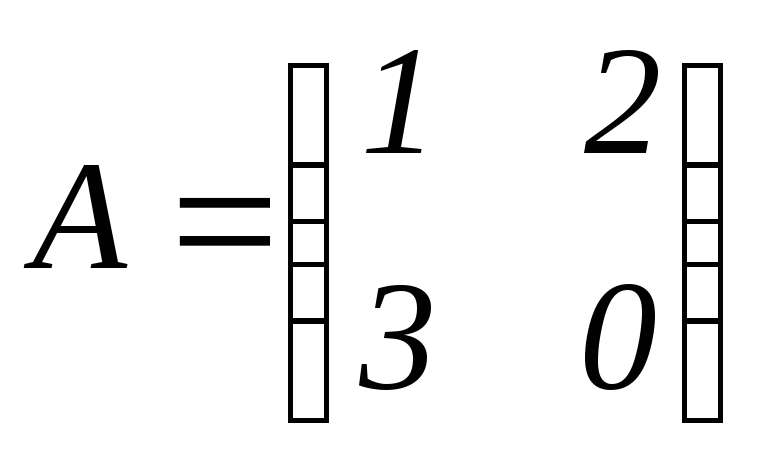 .
.
Решение.
![]() ,
,
![]() ,
,
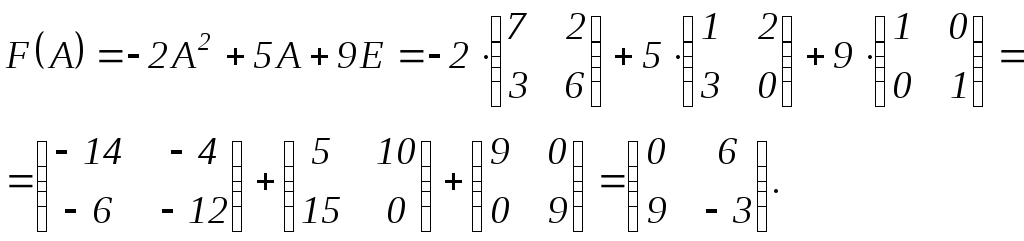
Транспонировать матрицу:
 .
.
Решение.
![]()
Вычислить определитель:
 .
.
Решение.
![]() .
.
 .
.
Решение.
 .
.
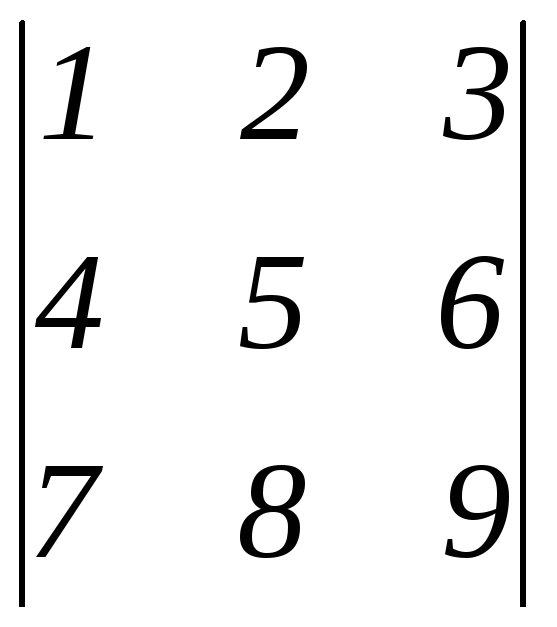 .
.
Решение.
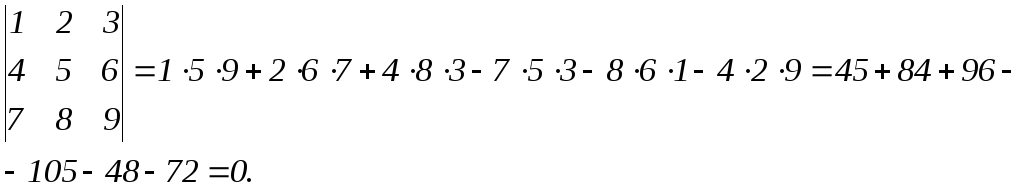
 .
.
Решение.
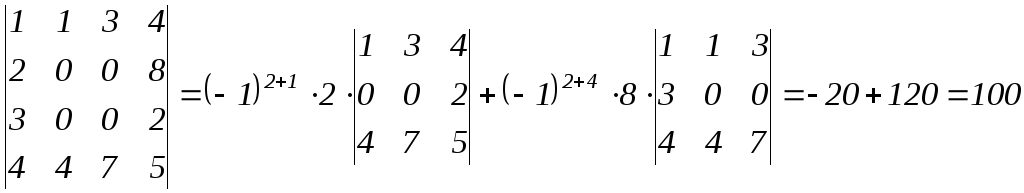 .
.
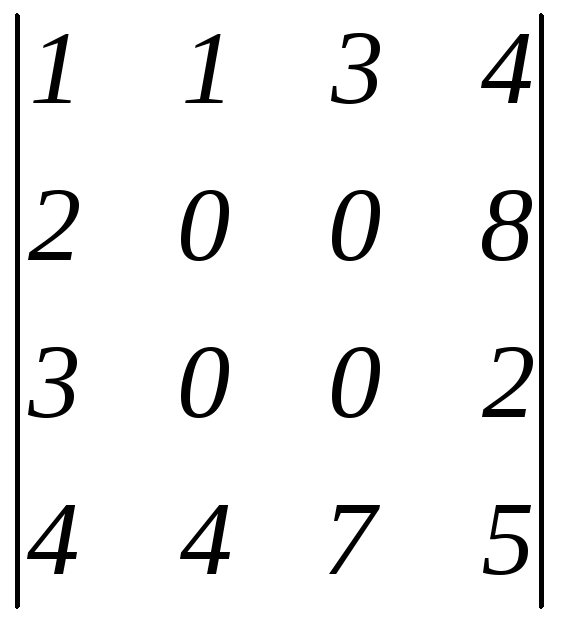
Найти ранг матрицы:
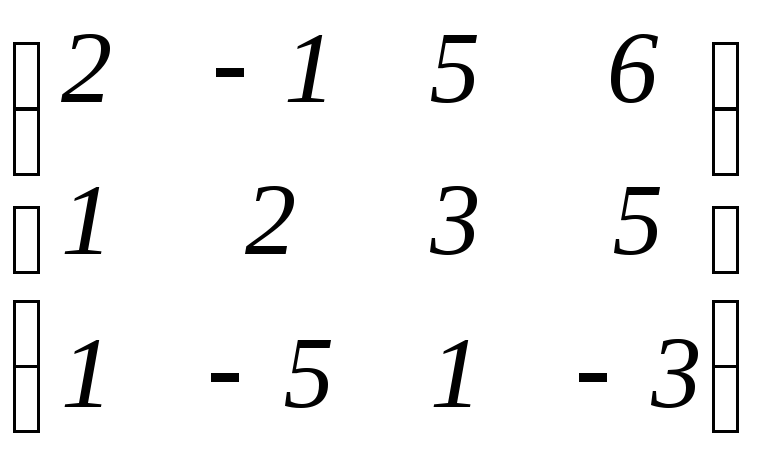 .
.
Решение.
Приводим матрицу к ступенчатому виду с помощью элементарных преобразований:
 ,
значит, ранг равен
,
значит, ранг равен
![]() .
.
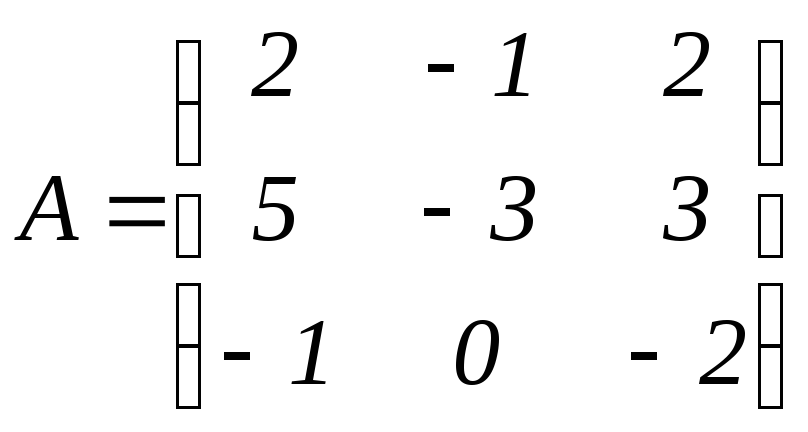
Найти обратную матрицу:
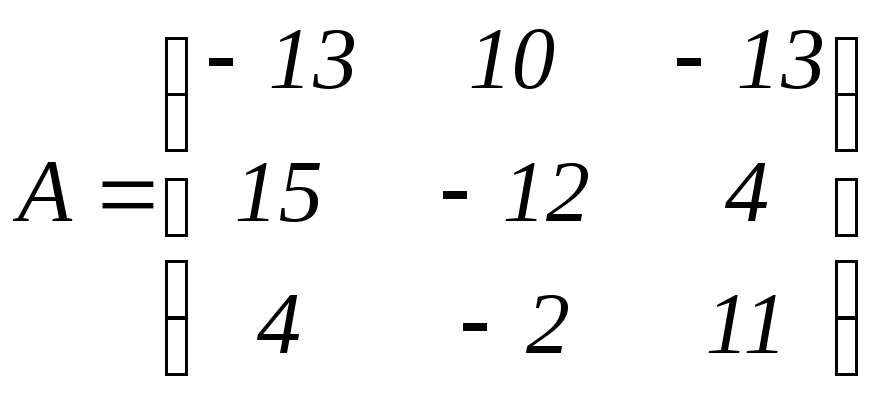 .
.
Решение.
Вычислим определитель матрицы А.
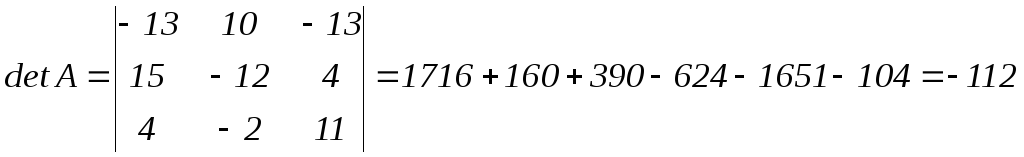 ,
,
определитель
матрицы А не равен 0, следовательно,
матрица А имеет обратную
![]() .
.
Найдём транспонированную
матрицу
![]() .
.
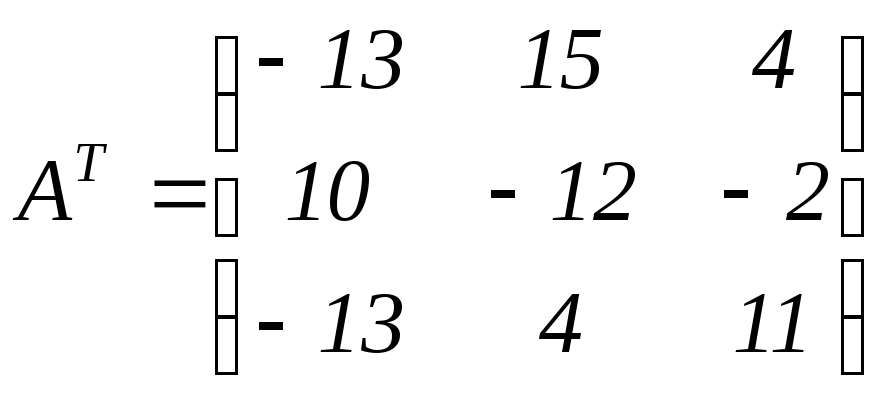 .
.
Найдем алгебраические
дополнения ко всем элементам матрицы
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Составляем обратную матрицу:
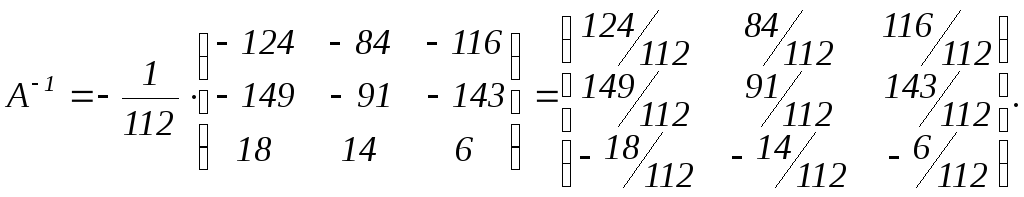
Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение:
Решение.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
![]()
Ранг матрицы
системы равен рангу расширенной матрицы
системы:
![]() ,
значит, система совместна. Количество
неизвестных также равно 2:
,
значит, система совместна. Количество
неизвестных также равно 2:![]() ,
значит система определена, то есть имеет
единственное решение. Запишем систему
уравнений, соответствующую полученной
расширенной матрице:
,
значит система определена, то есть имеет
единственное решение. Запишем систему
уравнений, соответствующую полученной
расширенной матрице:
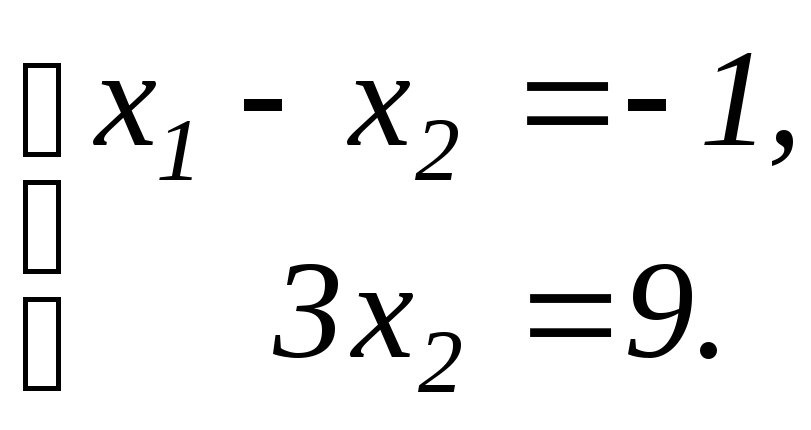 Получаем,
Получаем,
![]() ,
,![]() .
.
Решение.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:

Ранг матрицы
системы равен рангу расширенной матрицы
системы:
![]() ,
значит, система совместна. Количество
неизвестных не равно 2:
,
значит, система совместна. Количество
неизвестных не равно 2:![]() ,
значит, система неопределенна, то есть
имеет бесконечно много решение. Количество
главных переменных равно
,
значит, система неопределенна, то есть
имеет бесконечно много решение. Количество
главных переменных равно![]() ,
количество свободных переменных равно
,
количество свободных переменных равно![]() .
Выберем какой – нибудь, не равный 0,
минор второго порядка полученной
матрицы, например, минор
.
Выберем какой – нибудь, не равный 0,
минор второго порядка полученной
матрицы, например, минор![]() .
Тогда
.
Тогда![]() и
и![]() - главные переменные,
- главные переменные,![]() - свободная переменная. Запишем систему
уравнений, соответствующую полученной
расширенной матрице:
- свободная переменная. Запишем систему
уравнений, соответствующую полученной
расширенной матрице:
 Получаем,
Получаем,
![]() ,
,![]() .
.
Решить систему линейных уравнений методом обратной матрицы и по формулам Крамера:
Решение.
Решим систему методом обратной матрицы.
Введём матрицы:
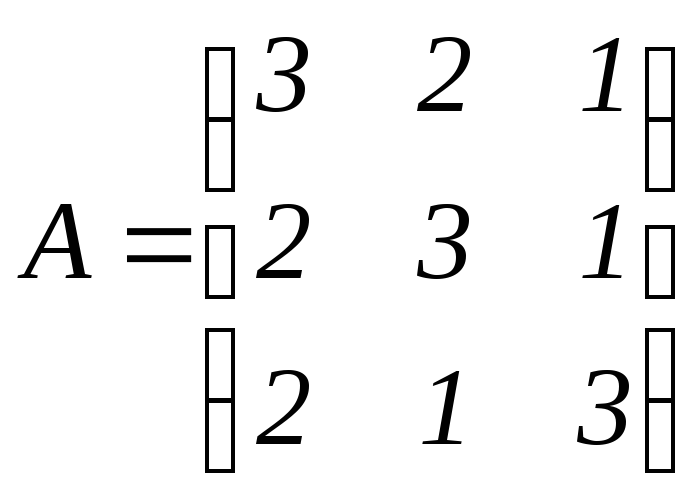 ,
,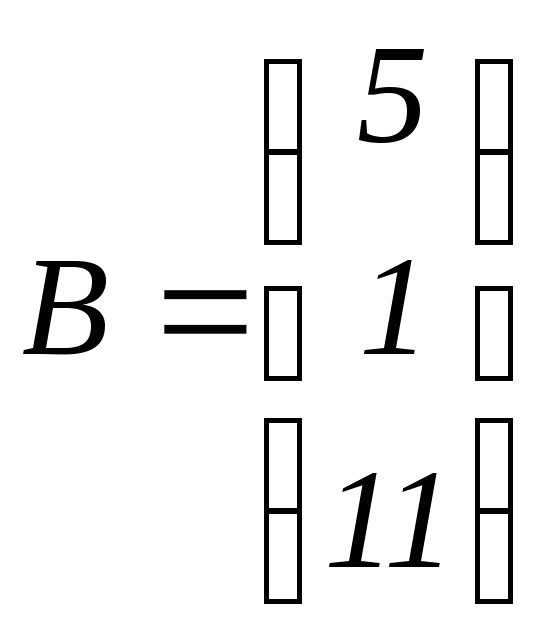 ,
,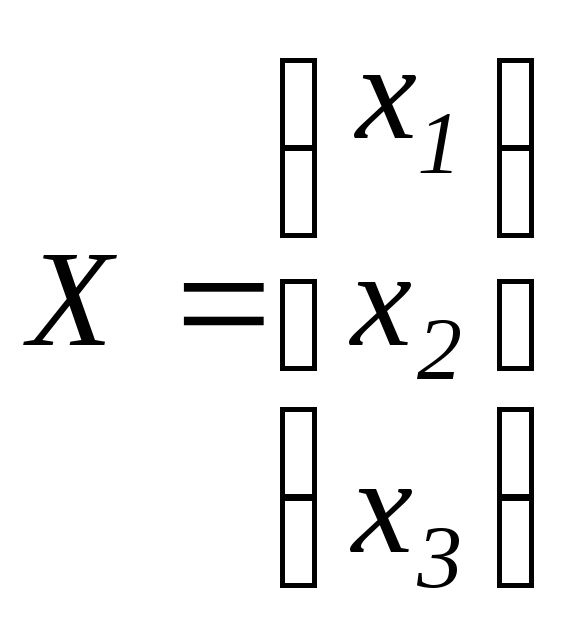 ,
тогда систему
,
тогда систему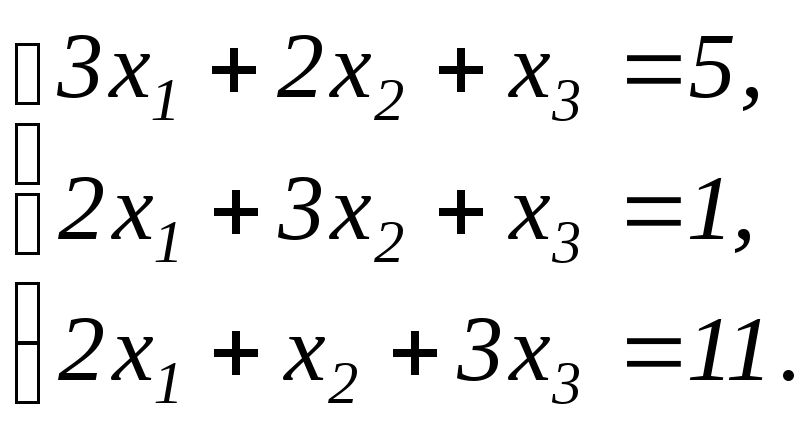 можно записать в матричном виде
можно записать в матричном виде![]() ,
откуда
,
откуда![]() .
.
Найдём определитель матрицы А:

значит, матрица А
имеет обратную
![]() .
Для нахождения присоединенной матрицы
.
Для нахождения присоединенной матрицы![]() вычислим алгебраические дополнения ко
всем элементам.
вычислим алгебраические дополнения ко
всем элементам.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда присоединённая
матрица
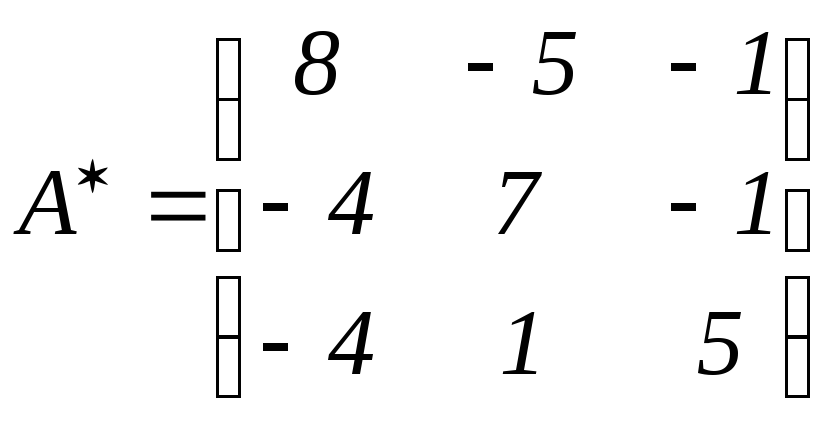 .
.
Обратная матрица
 .
Найдём решение
.
Найдём решение![]() :
:
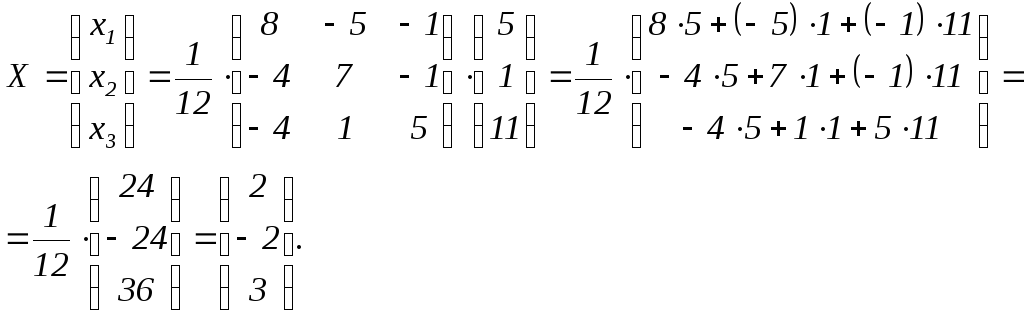
Решим систему методом Крамера.
Найдём главный
определитель системы
![]() :
:
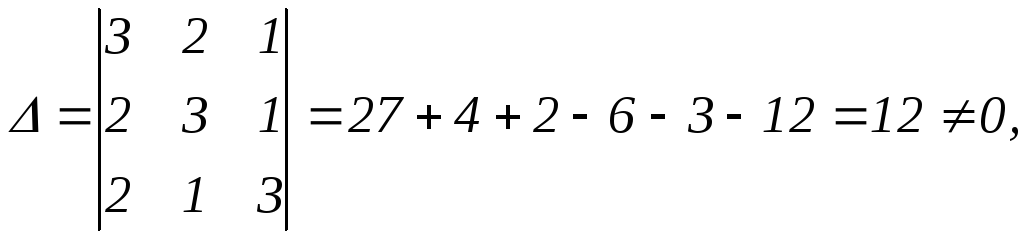 следовательно,
система совместна и имеет единственное
решение.
следовательно,
система совместна и имеет единственное
решение.
Найдём вспомогательные определители:

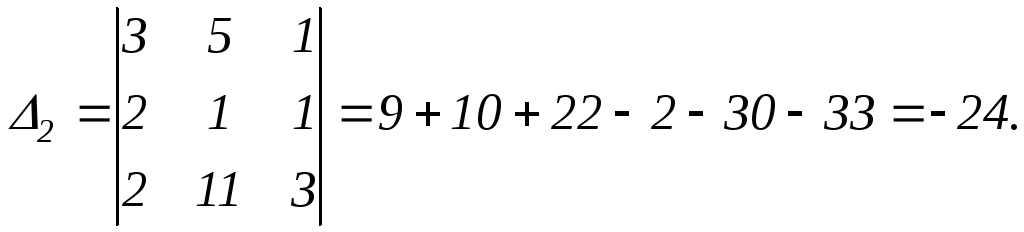
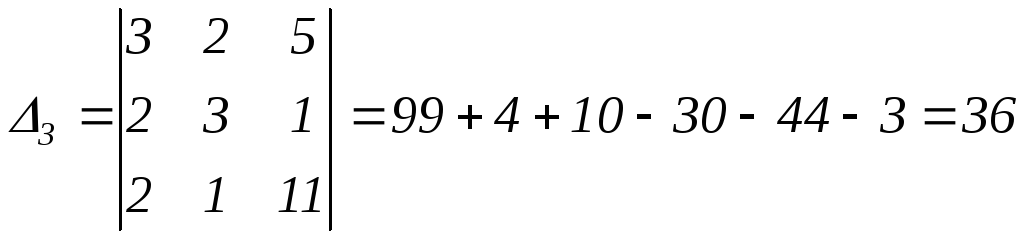 .
.
Найдём решение системы, используя формулы Крамера:
![]() ,
,
![]() ,
,![]() ,
,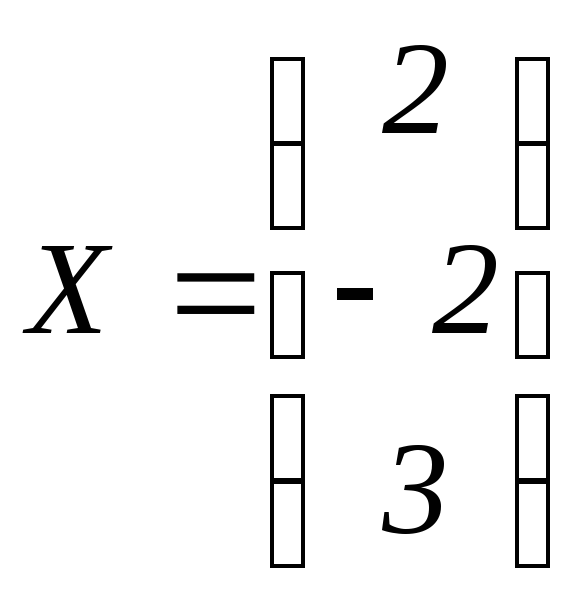 .
.
Решить систему методом Жордана – Гаусса:
1)

Решение.
Запишем коэффициенты и свободные члены в таблицу.
|
|
|
|
|
|
|
1 |
1 |
-3 |
2 |
6 |
|
1 |
-2 |
0 |
-1 |
-6 |
|
0 |
1 |
1 |
3 |
16 |
|
2 |
-3 |
2 |
0 |
6 |
В ыбираем
разрешающий элемент. Перепишем без
изменений строку, содержащую этот
элемент, а все элементы искомого столбца,
кроме разрешающего элемента, заменяем
нулями. Остальные элементы пересчитываем:
ыбираем
разрешающий элемент. Перепишем без
изменений строку, содержащую этот
элемент, а все элементы искомого столбца,
кроме разрешающего элемента, заменяем
нулями. Остальные элементы пересчитываем:
![]()
|
|
|
|
|
|
|
1 |
1 |
-3 |
2 |
6 |
|
0 |
- |
3 |
-3 |
-12 |
|
0 |
1 |
1 |
3 |
16 |
|
0 |
-5 |
8 |
-4 |
-6 |
Снова выбираем разрешающий элемент, игнорируя первый столбец и первую строку:
|
|
|
|
|
|
|
1 |
0 |
-4 |
-1 |
-10 |
|
0 |
0 |
6 |
6 |
36 |
|
0 |
1 |
1 |
3 |
16 |
|
0 |
0 |
13 |
11 |
74 |
Выбираем разрешающий элемент в четвёртой или второй строке:
|
|
|
|
|
|
|
1 |
0 |
- |
-1 |
-10 |
|
0 |
0 |
1 |
1 |
6 |
|
0 |
1 |
1 |
3 |
16 |
|
0 |
0 |
13 |
11 |
74 |
|
|
|
|
|
|
|
1 |
0 |
0 |
3 |
14 |
|
0 |
0 |
1 |
1 |
6 |
|
0 |
1 |
0 |
2 |
10 |
|
0 |
0 |
0 |
-2 |
-4 |
|
|
|
|
|
|
|
1 |
0 |
0 |
3 |
14 |
|
0 |
0 |
1 |
1 |
6 |
|
0 |
1 |
0 |
2 |
10 |
|
0 |
0 |
0 |
1 |
2 |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
8 |
|
0 |
0 |
1 |
0 |
4 |
|
0 |
1 |
0 |
0 |
6 |
|
0 |
0 |
0 |
1 |
2 |
Ответ:
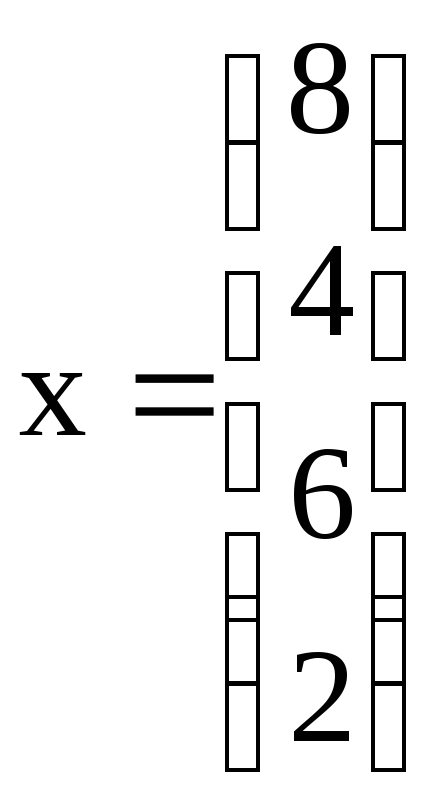 .
.
Заданы векторы
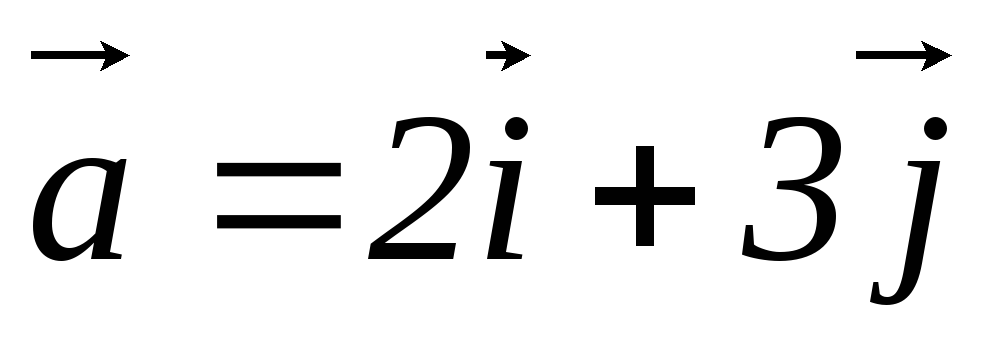 ,
,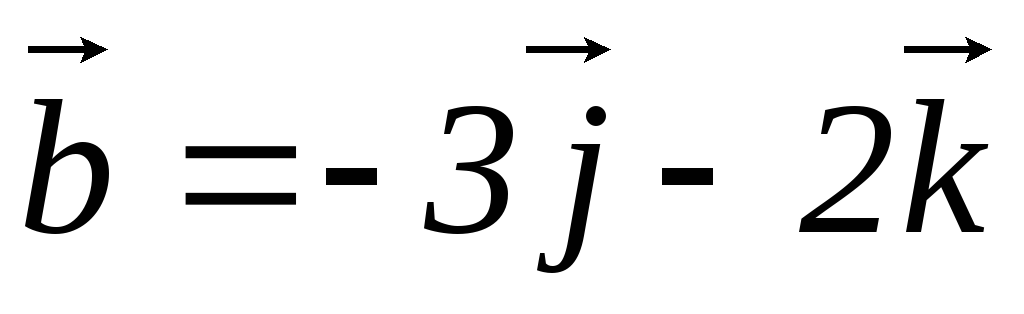 ,
,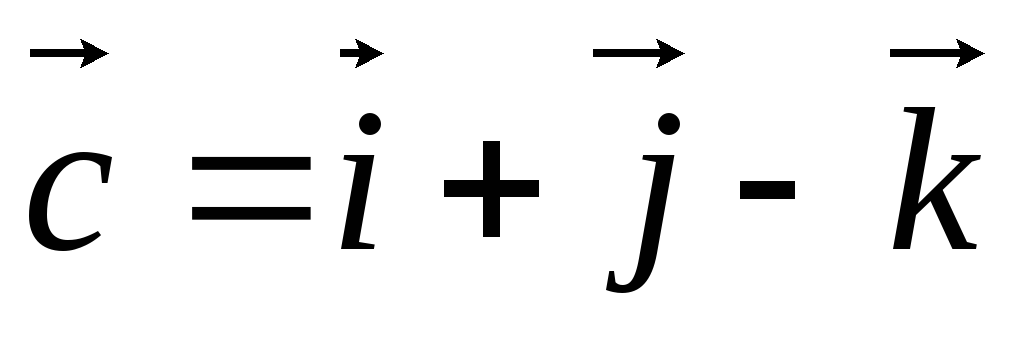 .
Найти:
.
Найти:
а) координаты
вектора
![]() ;
;
б) координаты
вектора
![]() ;
;
в) разложение
вектора
![]() по базису
по базису![]() .
.
Решение.
а) Так как
![]() ,
то найдем сначала длину вектора
,
то найдем сначала длину вектора![]() по формуле
по формуле![]() ,
,![]() .
Тогда
.
Тогда
![]() .
.
б) Вычислим координаты вектора
![]() ,
,
![]() .
.
в)
![]() .
.
Найти длину и направляющие косинусы вектора
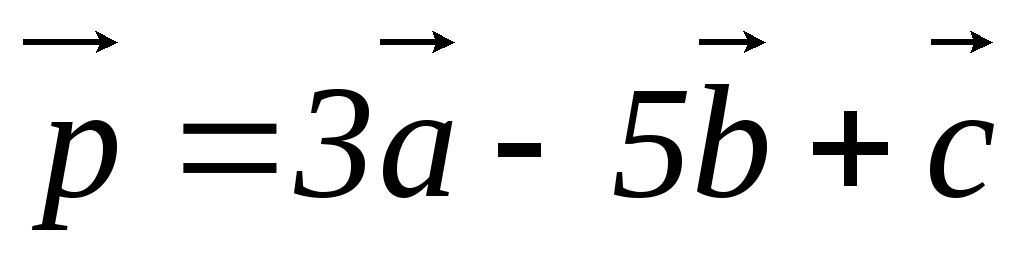 ,
если
,
если
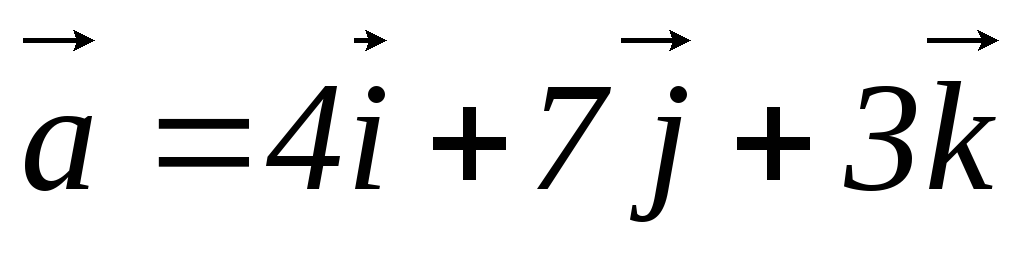 ,
,
 ,
,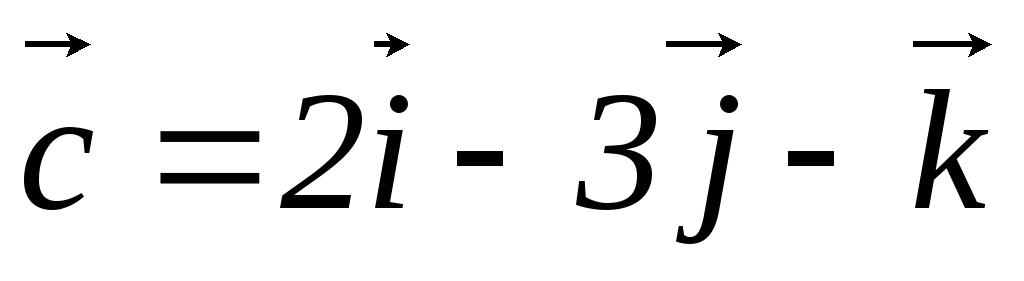 .
.
Решение.
Найдем разложение
вектора
![]() по базису
по базису![]() ,
,![]() ,
,![]() :
:
![]() .
.
Найдем длину
вектора
![]() :
:
![]() .
Тогда орт вектора
.
Тогда орт вектора
![]() - вектор
- вектор
![]() .
.
Известно, что
координаты орта вектора есть его
направляющие косинусы. Следовательно,
![]() ,
,![]() ,
,![]() .
.
Определить, при каких значениях
 ,
, векторы
векторы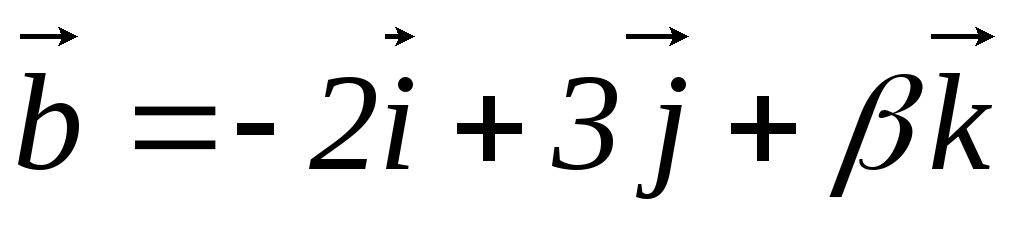 и
и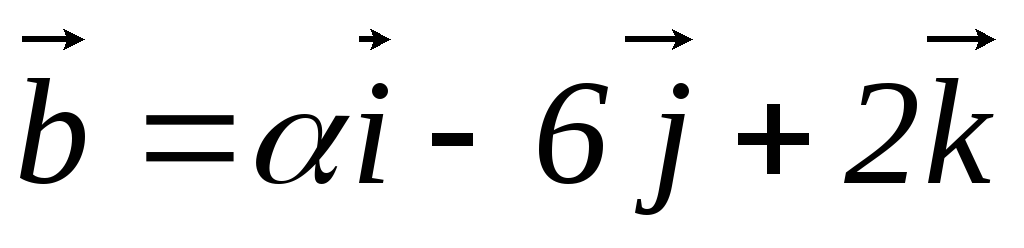 коллинеарны.
коллинеарны.
Решение.
Из условия коллинеарности двух векторов следуют равенства:
![]() .
Тогда
.
Тогда
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Даны векторы
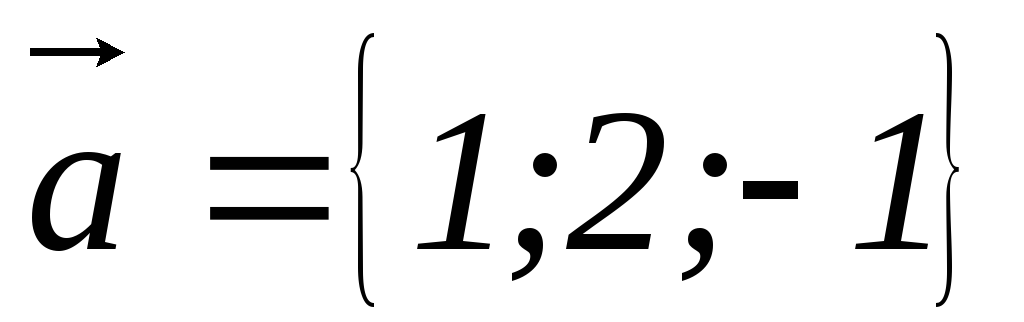 ,
,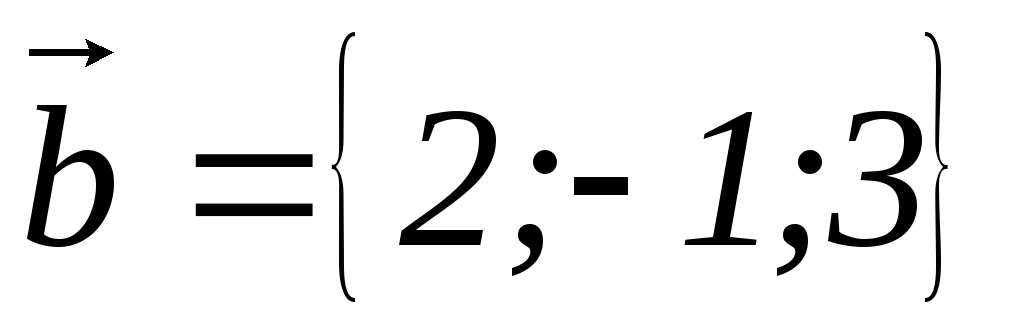 .
Найти
.
Найти .
.
Решение.
Так как
![]() ,
,
![]() .
.
Дано:
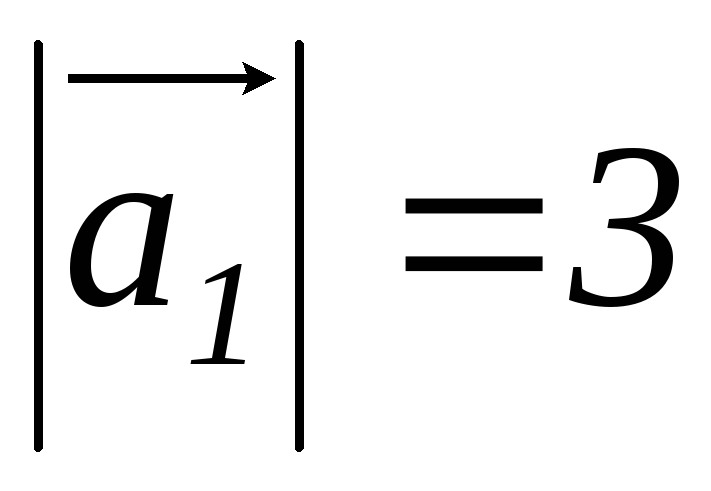 ,
,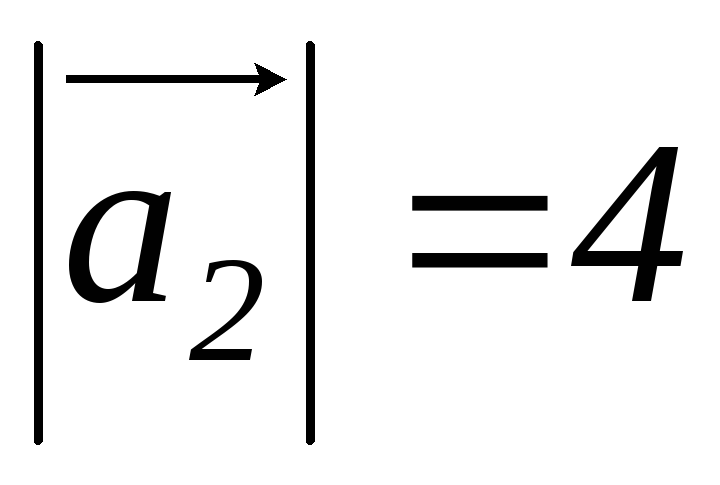 ,
,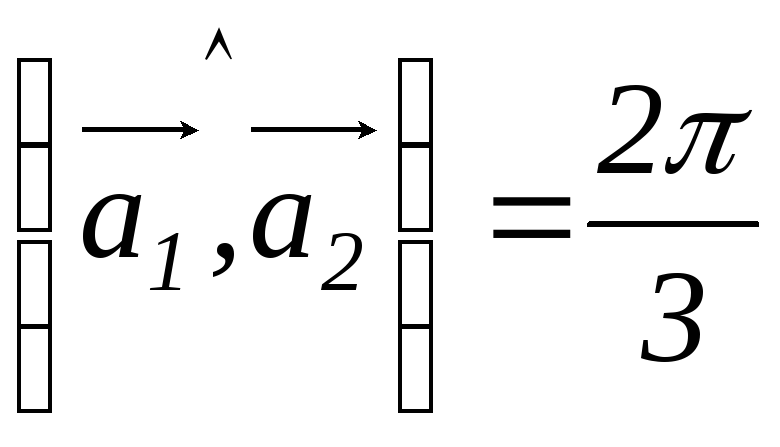 .
Вычислить: а)
.
Вычислить: а) ;
б)
;
б) ;
в)
;
в)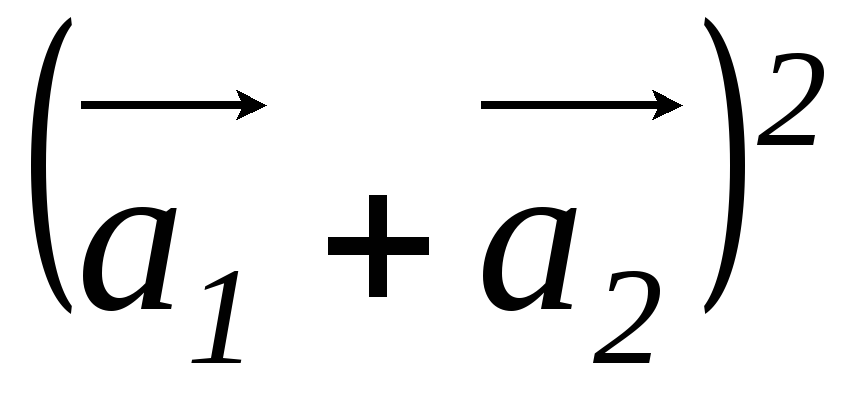 .
.
Решение.
а)
![]() ;
;
б)
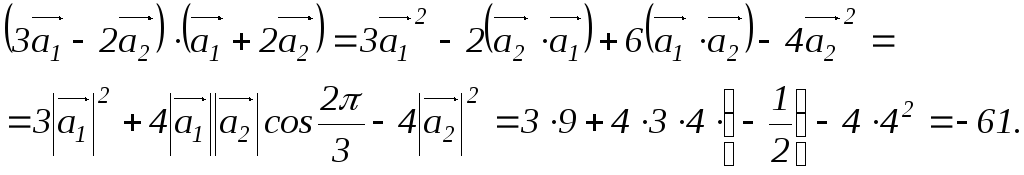
в)
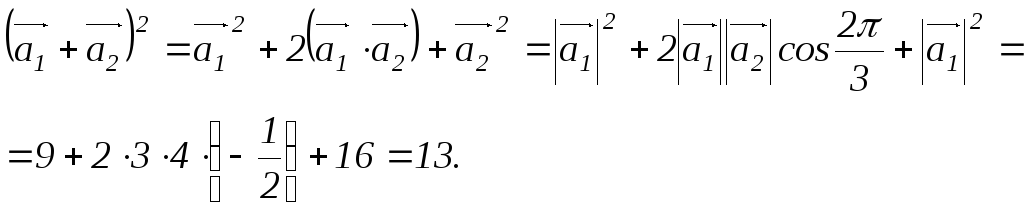
В плоскости
 найти
вектор
найти
вектор
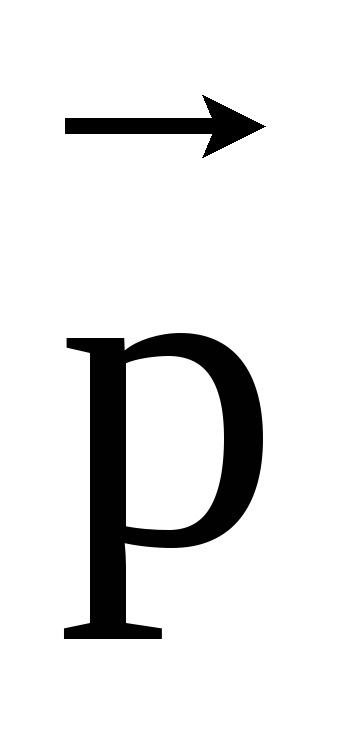 ,
перпендикулярный
,
перпендикулярный
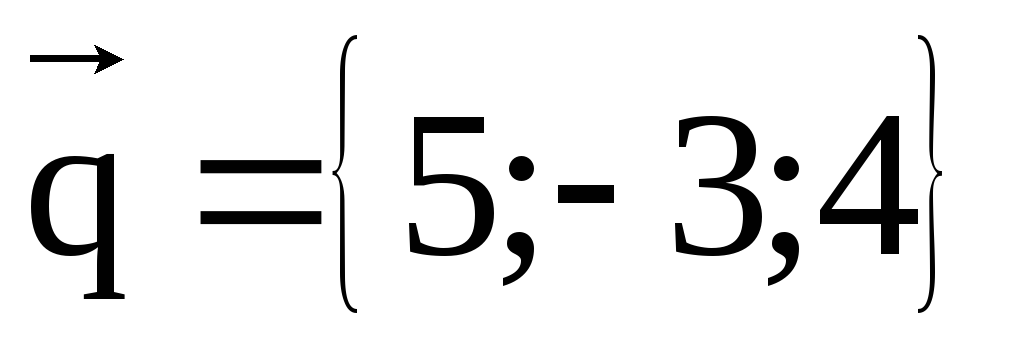 и имеющий одинаковую с ним длину.
и имеющий одинаковую с ним длину.
Решение.
![]() .
.
Возьмем
![]() и вычислим скалярное произведение
и вычислим скалярное произведение![]() (по условию), или
(по условию), или![]() .
Кроме того,
.
Кроме того,![]() .
.
Получаем систему уравнений:
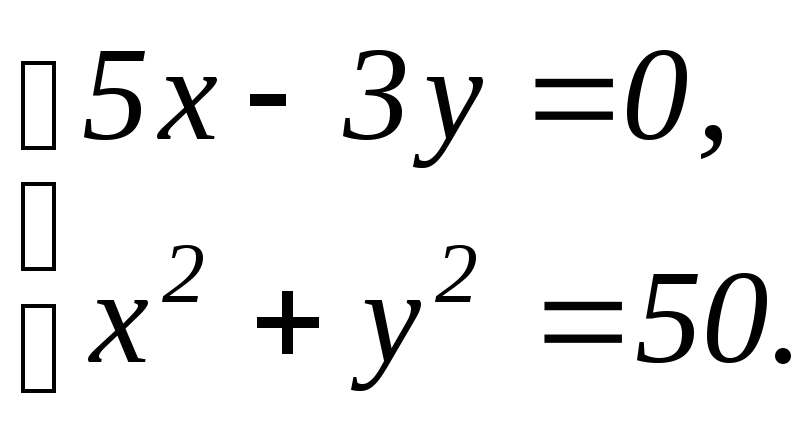
![]()
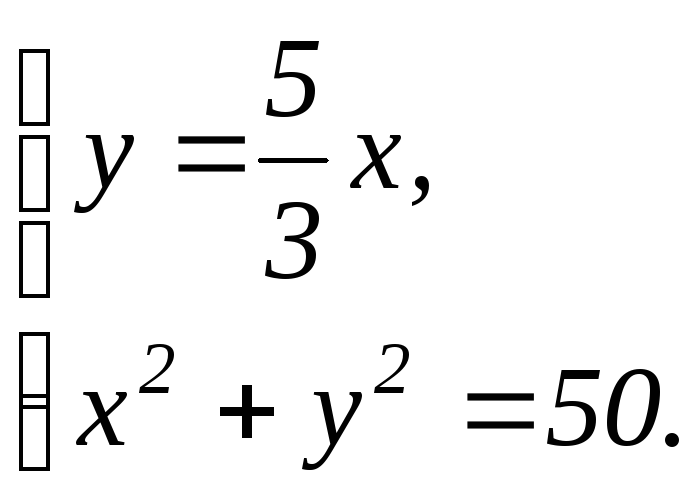
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,![]() .
.
Ответ:
![]() ,
,![]() .
.
Векторы
 и
и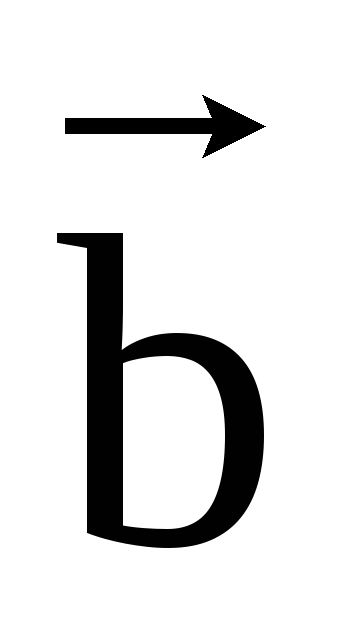 образуют угол
образуют угол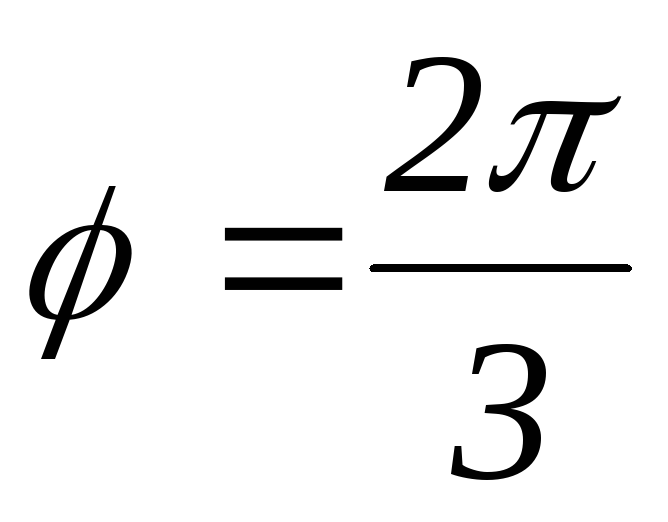 .
Зная, что
.
Зная, что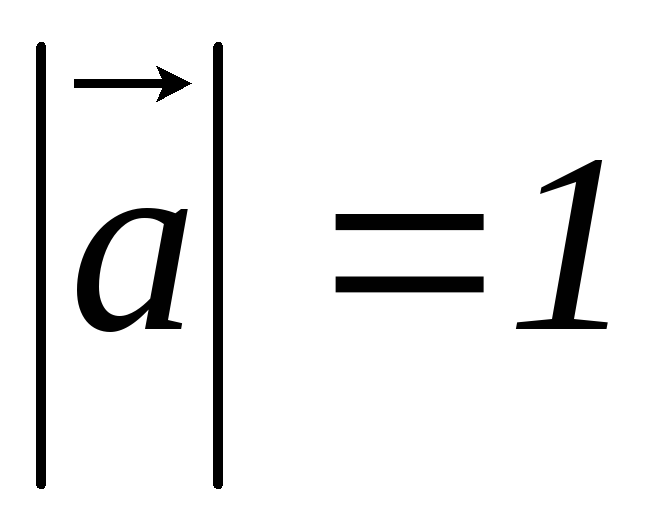 и
и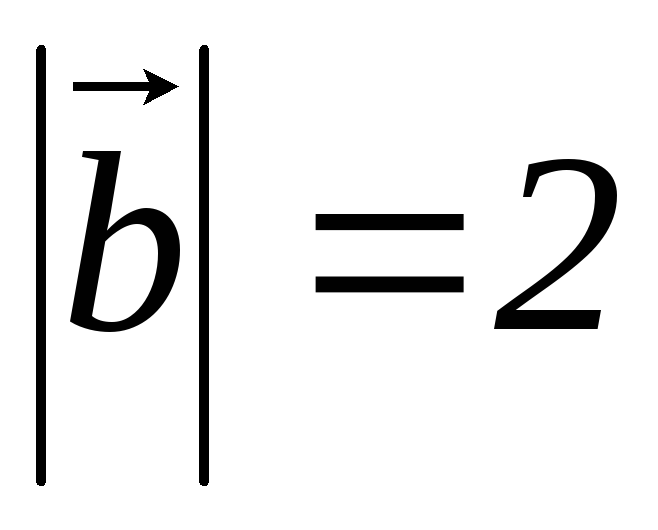 ,
вычислить: 1)
,
вычислить: 1) ;
2)
;
2)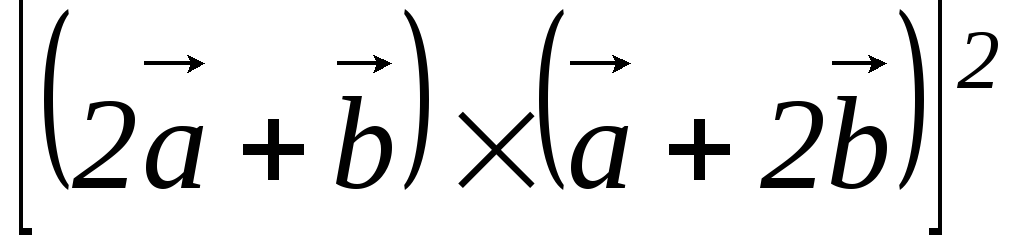 ;
3)
;
3)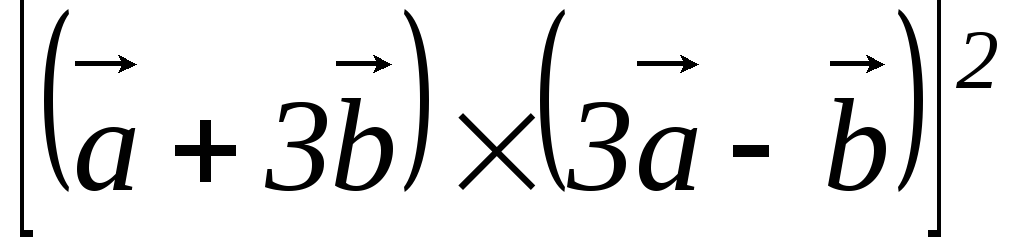 .
.
Решение.
1)
![]() .
.
2)
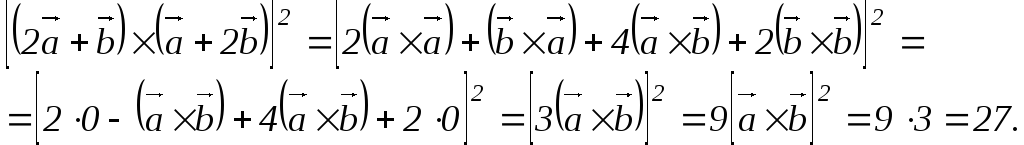
3)
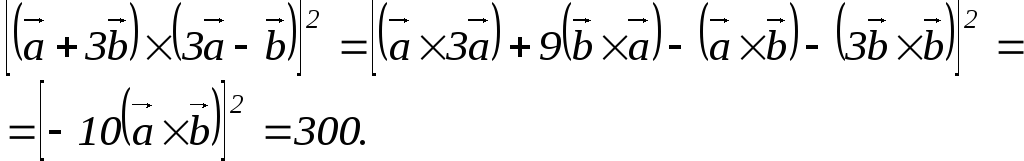
Найти собственные значения и собственные вектора матрицы
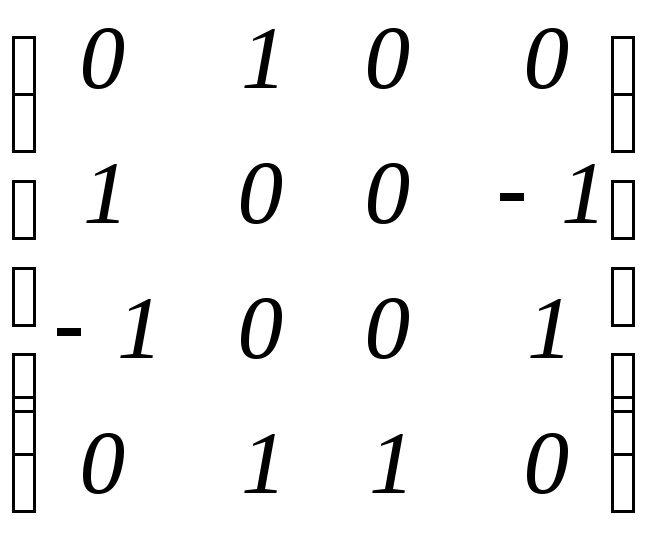 .
.
Решение.
Составляем
характеристическое уравнение:

Вычислим определитель разложением по первой строке:
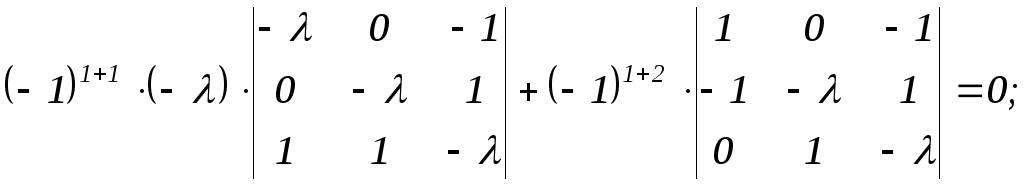
![]()
![]()
![]() ,
,
![]() ,
,![]() - собственные значения матрицы.
- собственные значения матрицы.
Найдём собственный
вектор
![]() ,
соответствующий собственному значению
,
соответствующий собственному значению![]() .
.
![]() или
или
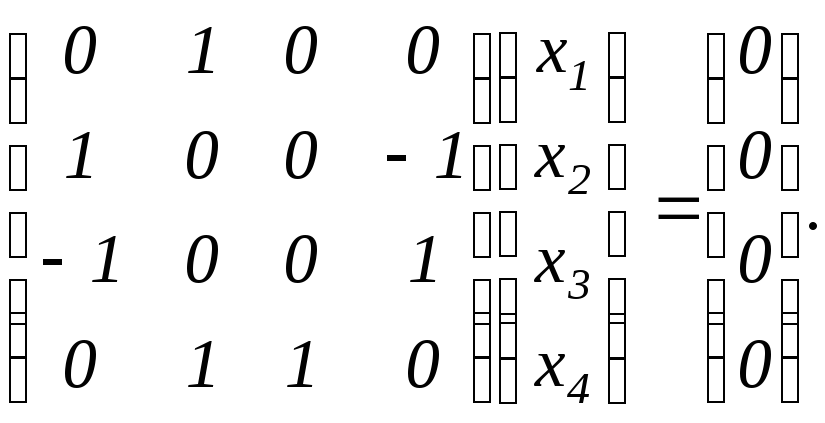
То есть

Решим данную систему.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
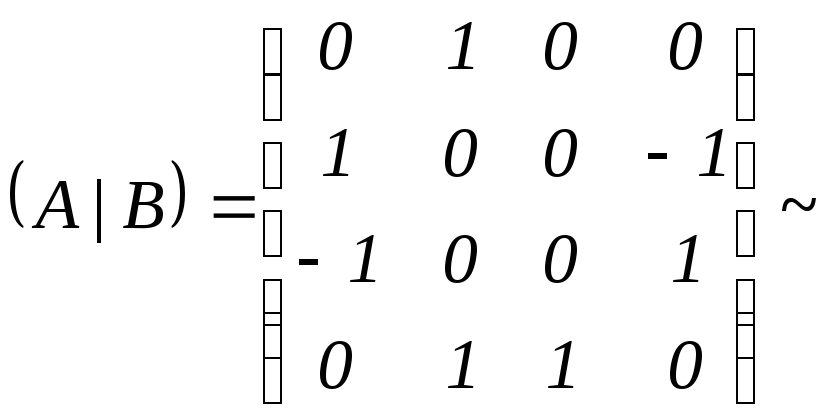
Поменяем первую и вторую строки местами:
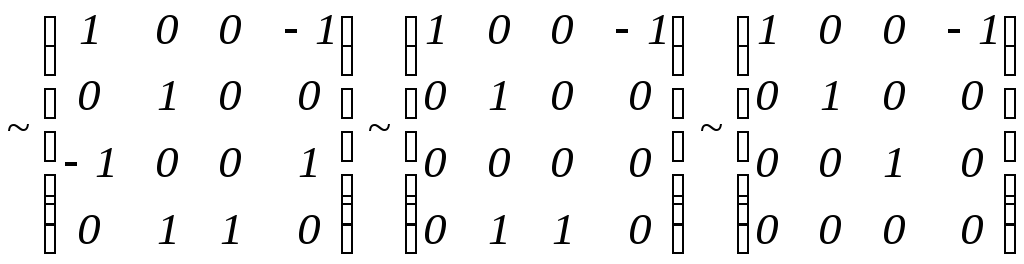 .
.
Имеем:
![]() ,
,![]() ,
,![]() .
.
Отсюда получаем
собственный вектор матрицы
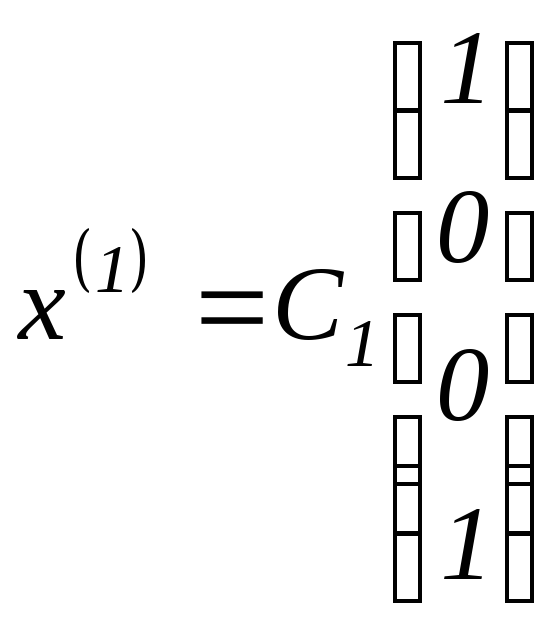 .
.
Найдём собственный
вектор
![]() ,
соответствующий собственному значению
,
соответствующий собственному значению![]() .
.
![]() или
или
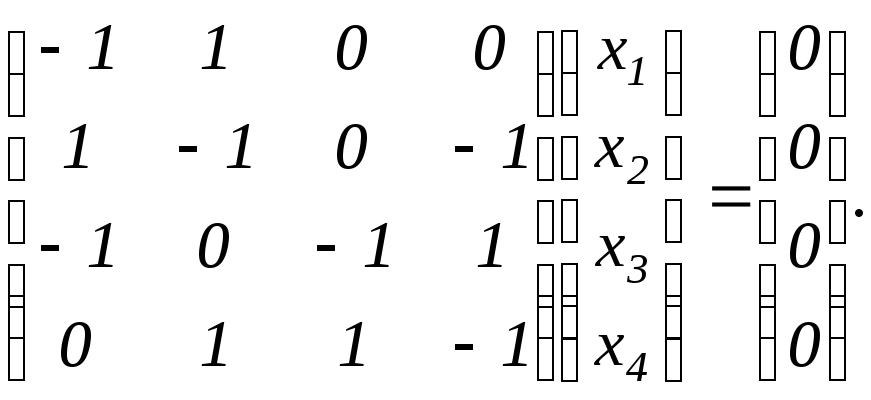
То есть

Решим данную систему.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
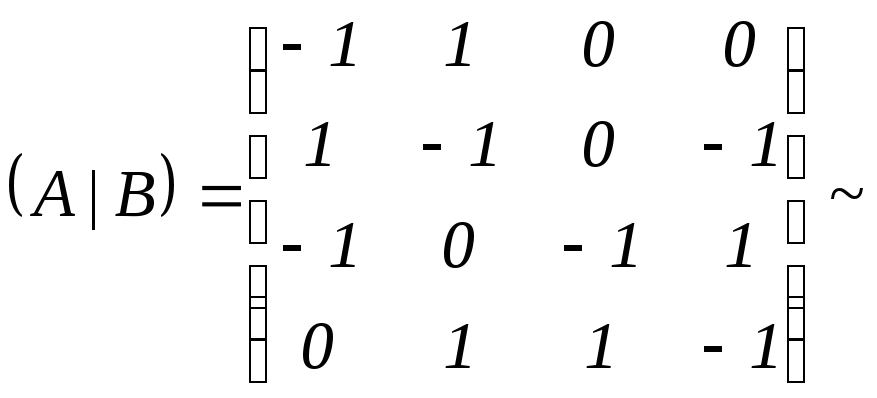
Поменяем первую и вторую строки местами:

Имеем:
![]() ,
,![]() ,
,![]() .
.
Отсюда получаем
собственный вектор матрицы
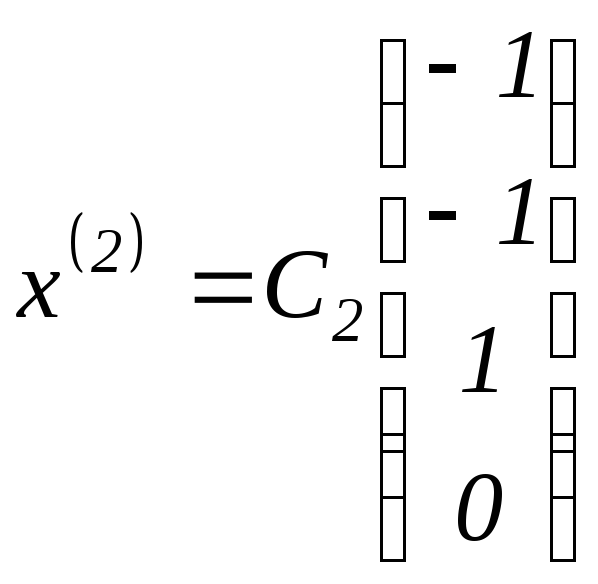 .
.
Найдём собственный
вектор
![]() ,
соответствующий собственному значению
,
соответствующий собственному значению![]() .
.
![]() или
или
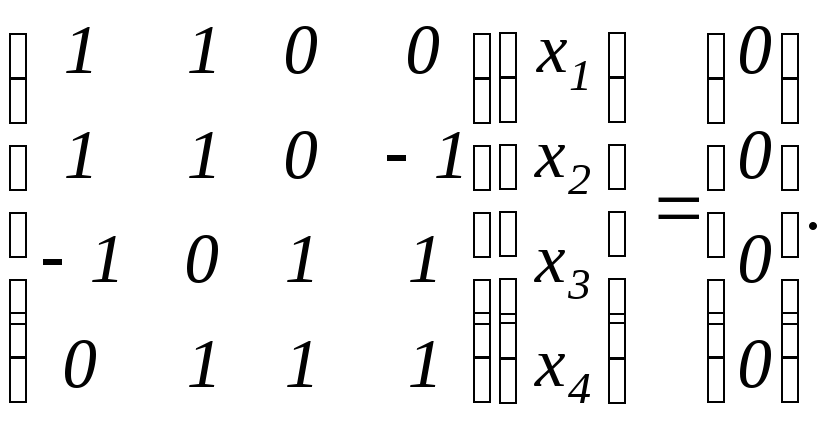
То есть
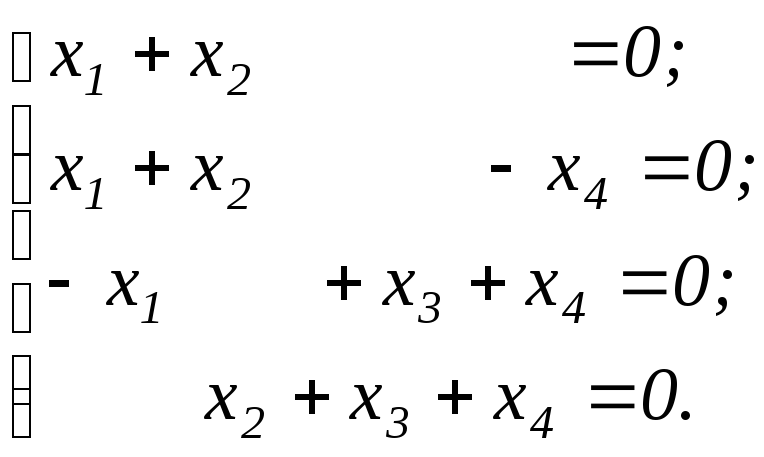
Решим данную систему.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:


.Имеем:
![]() ,
,![]() ,
,![]() .
.
Отсюда получаем
собственный вектор матрицы
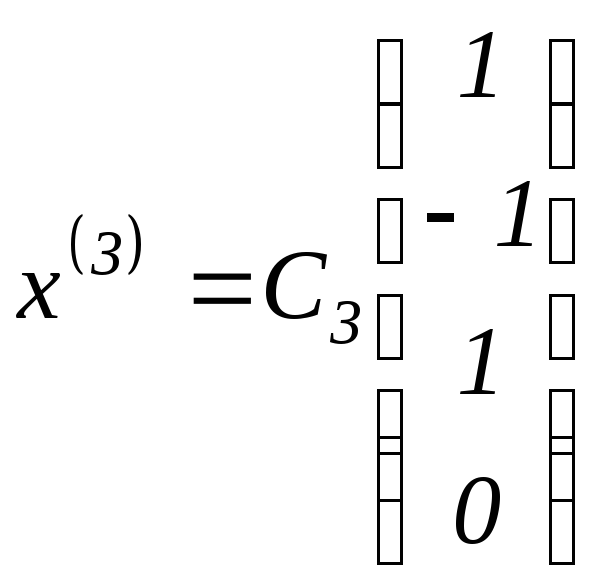 .
.
Найти линейное преобразование неизвестных, приводящих квадратичные формы, заданные своими матрицами к каноническому виду. Выяснить, является ли квадратичная форма знакоопределённой:
 .
.
Решение.
Имеем

Сгруппируем все
члены, содержащие
![]() ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
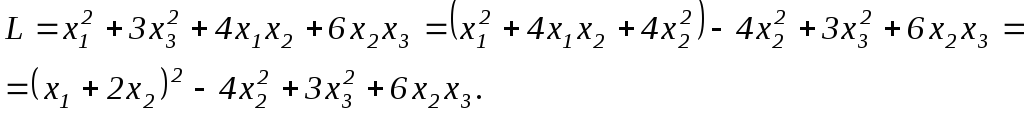
Сгруппируем все
члены, содержащие
![]() ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
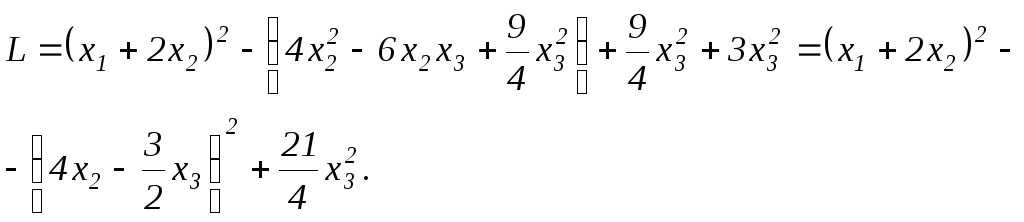
Таким образом,
невырожденное линейное преобразование
![]() ,
,![]() ,
,![]() приводит данную квадратичную форму к
каноническому виду
приводит данную квадратичную форму к
каноническому виду![]() .
.
Найдём все главные
угловые миноры матрицы:![]() ,
,![]() ,
,![]() .
Квадратичная форма не является
знакоопределённой по критерию Сильвестра
(она была бы отрицательно определённой,
если бы
.
Квадратичная форма не является
знакоопределённой по критерию Сильвестра
(она была бы отрицательно определённой,
если бы![]() ,
,![]() ).
).

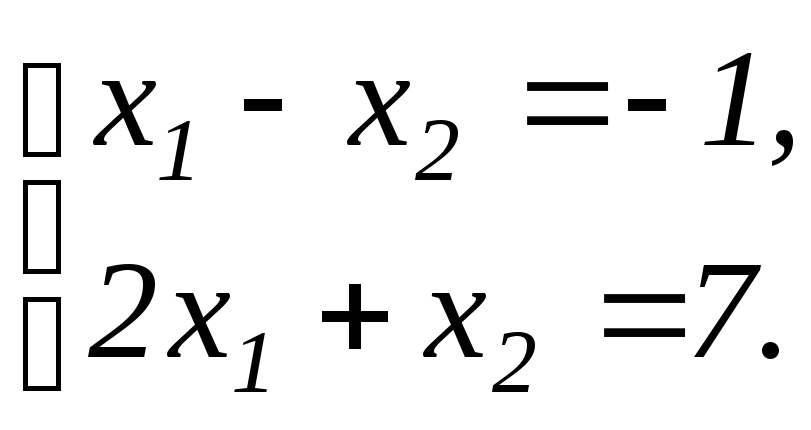

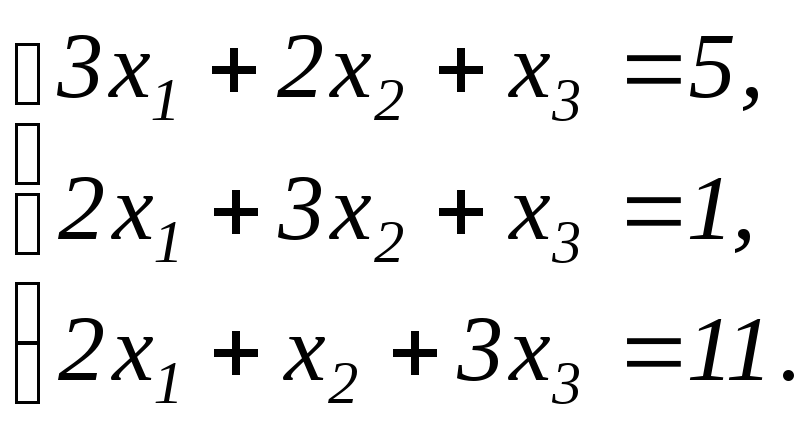


 3
3 4
4