1. Скалярное произведение векторов

(a,b)=ab^т=∑a_ib_i – скалярное произведение (алгебраическое представление)

ρ(a,b)=(∑(a_i-b_i)²)^1/2 – расстояние между векторами

║a║²=(a,a)=∑a_i²–норма вектора а (скалярное произведение вектора само на себя)

ρ(a,b)=(║a-b║)²)^1/2

║Af-U║²_Rn

Af– значение, вычисляемое по модели

U– экспериментальное значение

Расстояния между ними должны быть минимальными.

2. Скалярное произведение нормы функций. Расстояние между функциями.

(f,g)=∫f(x)g(x)dx–скалярное произведение функций.

Различие от скалярного произведения векторов в том, что здесь сумма заменена интегралом.

║f║²_L2=∫(f(x))²dx– норма функции

ρ(f,g)=(∫(f(x)-g(x))²dx)^1/2– расстояние между функциями

Расстояние между функциями = нулю когда f=g, когда они сильно отличаются расстояние будет большое.

Расстояние – сумма разностей значений этих функций в точке. Интеграл означает, что мы берем эти точки на бесконечно малом расстоянии.

ρ(f,g)=0

║f-g║²_L2

F– неизвестная функция

G– априорная информация, известная функция

Мы минимизируем расстояние между ними

║D(f-g)║²_L2– норма производных этих функций

║D(f-λg)║²_L2

λ- либо закругляет g, либо выпрямляет

3. Норма сеточной функции и ее представление виде квадратичной формы.

С

β1

β2

β3

еточная функция – мы набрасываем сетку и с каждым узлом этой сетки связываем функцию.

О

βi(x)

дна сплайн функция состоит из 4-х полигонов.

f(x)=∑f_iβ_i(x)

║f(x)║²_L2=∫(f(x))²dx=∫(f₁β₁+f₂β₂+….+f_nβ_n)(f₁β₁+f₂β₂+….+f_nβ_n)dx

bβ_1*β₁ β_1*β_{2 ……} β_1*β_ndxf₁

(f₁f₂…f_n) ∫ …

a β_n*β₁ β_n*β_{2 …...} β_n*β_nf_n

fQf^т– квадратичная форма

q_ij=∫β_i(x)*β_j(x)dx– элемент матрицыQ

q₀(n)=q_ij=∫β_i(x)*β_j(x)dx– матрица самих функций

q₁(n)=q_ij=∫β_i^’(x)*β_j^’(x)dx– матрица первых производных

q₂(n)=q_ij=∫β_i^’’(x)*β_j^’’(x)dx– матрица вторых производных

4. Скалярное произведение сеточных функций и расстояние между ними.

f(x)=∑f_iβ_i(x)

g(x)=∑g_iβ_i(x)

║f║²=fQf^т одно и то жеQ=Q

(f,g)=fQf^т

fq₀(n)g^т – в пространстве самих функций

fq₁(n)g^т – в пространстве первых производных

fq₂(n)g^т – в пространстве вторых производных

(f-g)Q(f-g)^т– расстояние между функциями

q_ij=∫β_i(x)*β_j(x)dx

5. Мнк. Постановка задачи. Система линейных уравнений.

min_(f)║Af-U║²_Rn– постановка задачи

Надо найти такое f, которое минимизирует данную норму.

R_n– размерность пространства.

A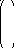– значение линейных функционалов от функций которые мы отыскиваем. Вычисляем в точках, где произведены измерения.

a₁₁ a₁₂ … a_1n f₁ = U₁

a₂₁ a₂₂ … a_2n f₂ = U₂

……………

a_n1 a_n2 … a_nn f_n

f=mnku(ab,cd,x,x1,x2…)

x– значения

x1 – первая производная

x2 – вторая производная

║Af-U║²=(Af-U)^т(Af-U)=(f^тA^т-U^т)(Af-U)=f^тA^тAf-f^тA^тU-U^тAf+U^тU=f^тA^тAf-2f^тA^тU+U^тU

(Af)^т=f^тA^т –при транспонировании в матричном случае компоненты необходимо менять местами

f^тA^тAf-2f^тA^тU+U^тU(*) – надо найтиminэтого выражения поf

Необходимо найти эту точку. Это min, где производная = 0

∂(*)/∂f=2A^тAf-2A^тU=0

Производная от f– единичный вектор =1

(f^тA^тAf)^т=1*A^тAf+f^тA^тA*1=2A^тAf

∂(*)/∂f=A^тAf-A^тU=0

A^тAf=A^тU– система уравнений, которую надо решить.

A^тA– симметричная матрица, т.е. не имеет значения с какой стороны находитсяf

f=(A^тA)/A^тU– решение системы уравнений, решение МНК

f=inv(A^тA)(A^тU) – обращение матрицы