Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Тюменский государственный нефтегазовый университет”

Институт нефти и газа

Методические указания и задания к практическим

занятиям по “Теории автоматического управления”

на тему “ Метод эквивалентной гармонической линеаризации” для студентов специальностей АТП и УИТС очной и заочной форм обучения

Тюмень 2004

Утверждено редакционно-издательским советом Тюменского государственного нефтегазового университета

Составители: к.т.н., доцент Макарова Л.Н., к.т.н. Макаров А.В.,

аспирант Фомин В.В.

Ответственный редактор: к.т.н., доцент Макарова Л.Н.

@ Государственное образовательное учреждение высшего

профессионального образования “ Тюменский государственный нефтегазовый университет”

Тюмень 2004

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Тюменский государственный нефтегазовый университет”

Институт нефти и газа

Методические указания и задания к практическим

занятиям по “Теории автоматического управления”

на тему “ Метод эквивалентной гармонической линеаризации” для студентов специальностей АТП и УИТС очной и заочной форм обучения

Председатель РИС Проректор

Перевощиков С.И. “ ” 200 г.

Рассмотрено на заседании

Подписи авторов Ученого совета ИНиГ

Протокол № от 200 г.

Подпись

Председатель совета

Рассмотрено на заседании

методической комиссии

Протокол № от 200 г

Подпись

Председатель метод. комиссии

Тюмень 2004

1. Краткие сведения и алгоритм метода эквивалентной гармонической линеаризации

Данный метод относится к приближенным методам исследования устойчивости автоколебаний нелинейных систем.

Его алгоритм:

1. Построить уравнение линейной части (при условии, что входной сигнал равен нулю);

2. Записать уравнение нелинейной части;

3. Построить линеаризованное уравнение замкнутой нелинейной системы;

4. Выделить в линеаризованном уравнении характеристическое уравнение, подставить в него 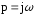и записать в первой форме комплексного числа:

;

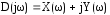5. Мнимую часть приравнять к нулю и найти значения частот, обеспечивающих это равенство (решить уравнение относительно ω) ;

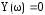6. Найденные значения 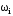подставить вX(ω;а) и приравнять X(а) к нулю:

X(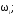а)=0

7. Из X(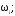а)=0 найти амплитуду автоколебаний (решить уравнение относительно а;

8. Проверить выполнение неравенства:

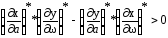
при каждой .

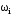Если неравенство для выбранного 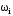, выполняется то— частота устойчивых автоколебаний; если неравенство не выполняется, то устойчивых автоколебаний с этой частотой нет.

2. Пример

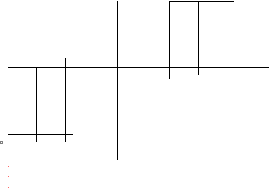
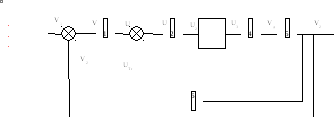
Исследовать устойчивость состояния системы, структурная схема которой приведена на (Рис.1).

Рис.1. Структурная схема: 1- чувствительный элемент; 2- релейный усилитель; 3- нелинейный усилитель; 4- исполнительный двигатель; 5- редуктор; 6- тахогенератор

Решение:

1. Составляем уравнения элементов структурной схемы:

1.1. Уравнение чувствительного элемента:

U₁=KV; V=V₁–V₂, где K— коэффициент усиления.

1.2. Уравнение релейного усилителя

(T₁P+1)U₂=K₂U; U=U₁–U_Tr, где K₂— коэффициент усиления,

T₁—постоянная времени.

1.3. Уравнение нелинейного усилителя

U₃=F(U₂) (Рис.2)

	U2 U3 c b -b -c
Рис.2. Характеристика нелинейного усилителя: b=0,25в; C=110в=U3max

1.4. Уравнение исполнительного двигателя

(T_mp+1)pV_д=K₃U₃, где V_д- угол поворота двигателя;

K₃- коэффициент передачи двигателя;

T_m- электромеханическая постоянная времени.

K₃=

Здесь U_3max— максимальное напряжение на выходе релейного усилителя;

N₀— скорость вращения холостого хода двигателя;

I— момент инерции всех вращающихся частей двигателя;

M₀— пусковой момент двигателя;

1.5. Уравнение тахогенератора

U_Tr=KU_pV_д, где K_U— крутизна статической характеристики тахогенератора.

1.6. Уравнение редуктора

V₂=K₅ V_д, где 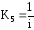, гдеi— передаточное число редуктора.

2. Дифференциальное уравнение линейной части имеет вид:

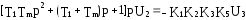
3. Для каждого вида нелинейности, в общем уравнении линеаризации, записывается зависимость выходной характеристики от входной:

U₃

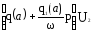
Значения q(a) и q₁(a) выбираются из таблицы (Прил.1.) в зависимости от вида нелинейности.

Для приведенной в примере нелинейности

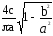q(a)=,a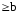

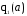=0, т.е. U₃=q(a)*U₂

4. Общее уравнение всей системы с учетом нелинейного звена и при отсутствии входного сигнала (равного нулю) имеет вид:

[Т₁Т_нр³+(Т₁+Т₂)р²+р+kg(a)]U₂=0, где k=k₁k₂k₃k₅.

Выделяем характеристическое уравнение:

D(p)=T₁T_Mp³+(T₁+T_M)p²+p+kg(a)=0.

5. Условие устойчивости в системе периодических решений вида U₂=Asinωt можно найти, используя критерий Михайлова.

Для этого в D(p) заменяется p на jω, выделяется в полученном выражении D(jω)=X(ω)+jY(ω) действительная и мнимая часть.

X(ω;a)=kg(a)–(T₁+T₂)ω²

Y(ω;a)=ω(1–T₁T_Mω²)

6. Мнимую часть приравнивается к нулю и находятся корни:

Y(ω;a)=0

ω(1–T₁T_Mω²)=0 => ω₁=0 , ω_2,3=±1/,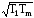

т.е. ω₁=0— Тривиальное решение,

Второе решение ω₂=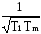

Найденное ω₂ подставляем в X(ω₀)=0

X(ω₂;a)=Kq(a)–(T1–T2)· 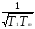=0, и учитывая, чтоq(a)=

=

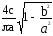
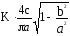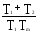
Полученное уравнение разрешается относительно a:

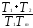
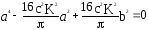
Найденное периодическое решение устойчиво, если выполняется неравенство при найденной частоте ω=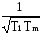

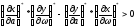
В нашем примере

=, ()

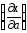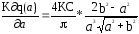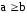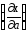=–2(T₁+T₂) ω

=1-3T₁T_m ω₂

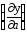=0

;

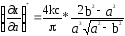
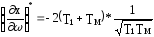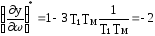
Проверяется условие устойчивости

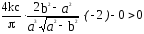(1)

2b²–a²<0 ; a>b.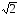

Для определения характера устойчивости проведем расчет для заданных значений параметров системы, а именно:

K₁=57,3 в/рад ; K₂=2,5 ; K₃=5,73 рад/в*с ; K₄=0 ; K₅=0,001 ; T₁=0,05c ; T_M=0,05c ; C=110в=U_зmax ; b=0,25в.

Квадратное уравнение:

0,4a⁴-616,6a²+3,85=0 , где 0,4= =0,1/0,5²

616,6=16·110²/π

3,25=(16·110²/π)·0,25²

имеет два корня

a₁=0.257 и a₂=2,86

Проверяется условие устойчивости автоколебаний при a₁=0,257;

b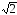=0.25*1.4=0.35; должно выполнятся неравенство a₁>b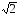; но 0,257<0,35, поэтому, a₁=0.257 не является амплитудой автоколебаний.

Проверяется условие устойчивости автоколебаний при a₂=2.86; 2,86>0.35 => a₂=2.86 — есть амплитуда автоколебаний с частотой:

ω=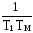=1/0,05=20 (1/с).

Замечание 1.

Частота автоколебаний во всей системе одинаковая, меняется ее амплитуда. Так, амплитуда

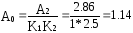
Замечание 2.

Амплитуда и частота автоколебаний зависит от параметров системы.

Так, в разобранном примере частота ω=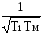, определяется постоянными времениT₁ и T_m; критическое значение амплитуды позволяет найти критическое значение коэффициента усиления.

Так как a>b, то критическое значение K_кр найдем из условия равенства a= b. Кроме того,

q(a)=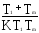, тогдаK_кр=

q(b)=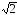

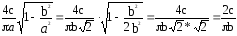
К_кр=

В рассматриваемом примере критическое значение коэффициента усиления линейной части системы равно:

K_кр=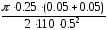=0.0057 (1/с)

Замечание 3.

Система с устойчивыми автоколебаниями можно привести в состояние устойчивого покоя (автоколебания отсутствуют), например, введением отрицательной обратной связи. Так, при K₄=10^-2 (в·с/рад) автоколебания в системе отсутствуют, ее состояние устойчиво.