Metodicheskie_ukazania Макарова / D-разбиение / D-разбиение

Министерство образования Российской Федерации Государственное образовательное учреждение профессионального высшего образования «Тюменский государственный нефтегазовый университет»

Ямальский нефтегазовый институт.

М Е Т О Д И Ч Е С К И Е У К А З А Н И Я И З А Д А Н И Я Д Л Я С А М О С Т О Я Т Е Л Ь Н О Й Р А Б О Т Ы

П О Т Е О Р И И У П Р А В Л Е Н И Я

«D-разбиения»

для студентов специальностей АТП и УИТС очной и заочной форм обучения

Председатель РИС	Проректор_________________
_______ (Перевощиков С. И.)	«____» ______________200_ г.
	Рассмотрено на
	заседании Учёного
	Совета ОНГИ
	Протокол № ____от___200 _г.
	Подпись _________________
	( Председатель Совета )
	Рассмотрено на
	Заседании методической
	комиссии института
	ЯНГИ
	Протокол № ____от___200 _г.
	Подпись _________________
	( Председатель метод. комиссии)

Новый Уренгой 2002

1. Постановка задачи

Критерии устойчивости позволяют не только сделать заключение о характере устойчивости системы при заданных параметрах, но и выяснить степень влияния их на устойчивость, определить предельные значения коэффициента усиления и времени запаздывания.

Разработаны специальные методы исследования. К ним относятся метод корневого годографа, метод D-разбиения.

2.Метод D-разбиения

2.1.Пусть система описывается характеристическим уравнением n-ой

степени:

A(p) = an pn + an-1 pn-1 + an-2 pn-2 + … + a0 = 0

При заданных коэффициентах уравнение имеет вполне определённые корни, пусть m – в правой полуплоскости; (n - m) – корни в левой полуплоскости.

При изменении коэффициентов корни перемещаются в плоскости корней. Это перемещение называется корневым годографом. При некотором сочетании коэффициентов корень может попасть в начало координат или на мнимую ось, тогда значения коэффициентов подчиняются характеристическому уравнению (an = 1):

A(jω ) = (jω )n + an-1 (jω )n-1 + … + a0 = 0

Это уравнение в (n-1) – мерном пространстве коэффициентов, по осям которого отложены а0 … аn-1 при заданном значении ω соответствует точка, а при изменении ω – гиперповерхность.

Если изменять коэффициенты, то при некотором сочетании их произойдет пересечение гиперповерхности А(jω ) = 0, следовательно, один или пара мнимых корней перейдет из правой (левой) полуплоскости в левую (правую) полуплоскость. Наиболее простой вариант, когда степень характеристического уравнения не превышает трех (n ≤ 3).

2.2. Разбиение по одному комплексному параметру. 3

Для выяснения влияния какого-либо параметра на устойчивость системы, если он входит в характеристическое уравнение линейно, придерживаются следующего алгоритма:

2.2.1.Представить характеристическое уравнение в виде А(р) = Р(р) +

ϑQ(р), где: ϑ - исследуемый параметр.

2.2.2.Определить границы D-разбиения, для этого заменить р на jω :

А(jω ) = Р(jω ) + ϑ Q(jω )

2.2.3. Выразить параметр ϑ из уравнения границы D-разбиения и представить его в алгебраической форме комплексного числа

ϑ = - P (jω ) = Х + jY

Q (jω )

2.2.4.Изменяя ω от 0 до + ∞ , построить половину границы.

2.2.5.В силу симметричности относительно действительной оси границы D-разбиения построить вторую половину границы, соответствующую

изменению ω от - ∞ до 0.

2.2.6.Провести штриховку полученной границы слева при движении по границе в сторону увеличения частоты.

2.2.7.Определить устойчивость системы в области с внутренней

штриховкой (рис.1), выбирая самое простое значение ϑ , например ϑ = 0 (по любому критерию).

а)	б)
	4

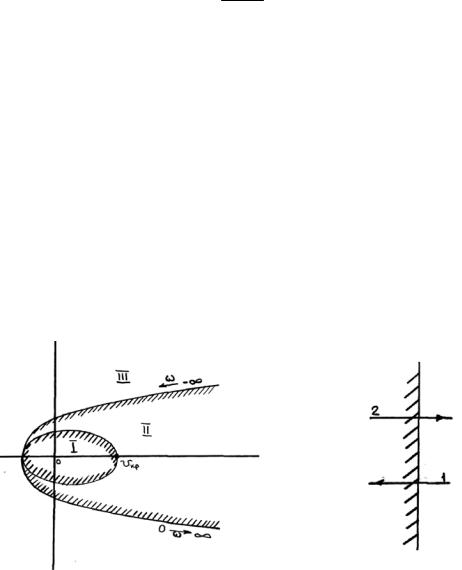
Рис.1 Пример области D-разбиения: I – область с внутренней штриховкой.

2.2.8.Если система устойчива в области I, то определяют число правых корней в других областях, руководствуясь правилом:

Если пересечение границы происходит по направлению штриховки (направление 1 на рис.1б), то один корень в плоскости D-разбиения переходит из правой полуплоскости в левую; если против штриховки (направление 2), то один корень переходит из левой полуплоскости в правую. Так на рис.1 в области II – один правый корень, в области III – два правых корня.

2.2.9.Для линейных задач определяют вещественный диапазон

изменения параметра (0; ϑ кр)

2.3. Пример 1. Дано характеристическое уравнение

(1 + Т1 р) (1 + Т2р) (1 + Т3р) + к = 0

Т1, Т2, Т3 – заданные постоянные времени; к – общий коэффициент усиления.

Замечание 1. Система состоит из трех инерционных звеньев. Определить значения к, при которых система будет устойчива. Решение.

2.3.1. ϑ	= -			k
			+ jω Т1 ) (1	+ jω	Т2 ) (1 + jω Т3 )
	(1

2.3.2.Раскрываем скобки и приводим к виду: X + jY:

к = [ω ² (Т1Т2 + Т1Т3 + Т2Т3) – 1] + j [ω ³ Т1Т2 Т3 – ω (Т1 + Т2 + Т3)] 2.3.3. Изменяя ω , построим границу D-разбиения (рис.2)

5

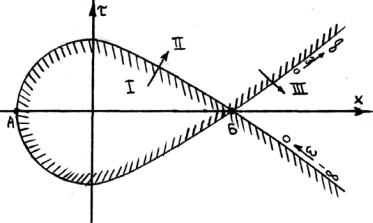
Рис.2 Граница D-разбиения для примера 1: I – область, претендующая на устойчивость; II – область, где число правых корней увеличивается на один;

III– область, где число правых корней увеличивается на 2 по сравнению с I.

2.3.4.Определяем устойчивость при ϑ = 0, характеристическое уравнение обращается при этом в уравнение (1 + Т1р) (1 + Т2р) (1 + Т3р) = 0.

	Оно имеет корни р1 = -	1	;	р2 = -	1	;	р3 = -	1	, т.е. все
		Т1			Т2			Т3

отрицательные, следовательно, система устойчива.

2.3.5. Система устойчива при изменении к от 0 до точки Б.

Замечание 2. Система устойчива и при отрицательных значениях к от точки А до точки 0, что соответствует положительной обратной связи.

2.4. Разбиение по двум параметрам.

Применяется тогда, когда необходимо выяснить влияние на устойчивость двух параметров одновременно.

Если параметры входят в характеристическое уравнение линейно, то

придерживаются следующего алгоритма:
2.4.1.Преобразуют характеристическое уравнение к виду
τ Р (р) + ν Q (р) + R (р) = 0 ,
где: τ и ν - параметры;
P (р); Q (р); R (р) - многочлены.
2.4.2. Граница D-разбиения в плоскости τ и ν	определяются
6

уравнением:

τР (jω ) + ν Q (jω ) + R (jω ) = 0

2.4.3.Вводят обозначения

Р (jω ) = Р1 (ω ) + j Р2 (ω ) Q (jω ) = Q1 (ω ) + j Q2 (ω )

R (jω ) = R1 (ω ) + j R2 (ω )

2.4.4. Если комплексное число равно нулю, то равны нулю действительная и мнимая его части, т.е.

τР1 (ω ) +ν Q1 (ω ) = - R1 (ω )

τР2 (ω ) +ν Q2 (ω ) = - R2 (ω )

2.4.5. Решая систему, определяют τ

и ν

τ

=

∆ τ

; ν =

∆ ν

∆

∆

∆

1

=

Р1 (ω ) Q1 (ω )

∆

τ

=

− R1 (ω ) Q1 (ω )

∆

ν 1

=

Р1 (ω ) − R1 (ω )

Р2 (ω ) Q2 (ω )

− R 2 (ω ) Q2 (ω )

Р2 (ω ) − R 2 (ω )

2.4.6.Изменяя ω , вычисляют сооветствующие τ (ω ) и ν (ω ), получая границу D-разбиения.

2.4.7.Если ∆τ ≠ 0; ∆ν ≠ 0, а ∆ = 0, то граница уходит в бесконечность.

2.4.8.Если ∆ = 0; ∆τ = 0, ∆ν = 0, то это особые прямые τ (ν ) и ν (τ ), практически они получаются при ω = 0 или ω → ∞ .

2.4.9.Штриховку границы D-разбиения выполняют по правилу:

-слева при обходе в сторону возрастающих ω , если ∆ > 0;

-справа при обходе в сторону возрастающих ω , если ∆ < 0;

-штриховка двойная, т.к. граница D-разбиения совпадает для положительных и отрицательных частот.

-особые линии (при ω = 0 и ω = ∞ ) имеют одинарную штриховку, которая должна вблизи точки сопряжения совпадать с двойной штриховкой, т.е. заштрихованные и незаштрихованные стороны обычной границы и особой линии совпадали.

7

-если ∆ = 0, но ω ≠ 0 (очень редкий случай), то штриховка по сформулированному правилу, но двойной штриховкой.

-если ω ≠ 0; ∆τ = 0; ∆ = 0, но проходя через нуль ∆ знак не меняет, то такая особая прямая не штрихуется, из рассмотрения выбрасывается.

2.5. Пример 2. Дано характеристическое уравнение

А(р) = (1 + р Т1) (1 + р Т2) (1 + р Т3) + к = 0,

в котором постоянная времени Т1 = τ ; коэффициент усиления к = ν могут варьироваться. Определить влияние изменения этих параметров на устойчивость системы.

Решение.

2.5.1. Выделим параметры ν и τ :

τ[(Т2Т3 р³ + (Т2 + Т3) р² + р] + ν + Т2 Т3 р² + (Т2 + Т3) р + 1 = 0

2.5.2.Заменим р на jω

Р (jω ) = [Т2 Т3 (jω )³ + (Т2 + Т3) (jω )² + jω ] Q (jω ) = 1

R (jω ) = Т2Т3 (jω )² + (Т2 + Т3) (jω ) + 1 - τ (Т2 + Т3) ω ² + ν = - Т2 Т3 ω ² τ (- Т2 Т3 ω ³ + ω ) = (Т2 + Т3) ω

∆ = (Т2 Т3 ω ² - 1) ω

	τ	=		T2 + T3
			T T ω 2 − 1
		2		3
	ν	= T2		T3 ω 3 − 1 +		(T + T )2			ω 2
						2	3
						T T ω 2		− 1
						2	3

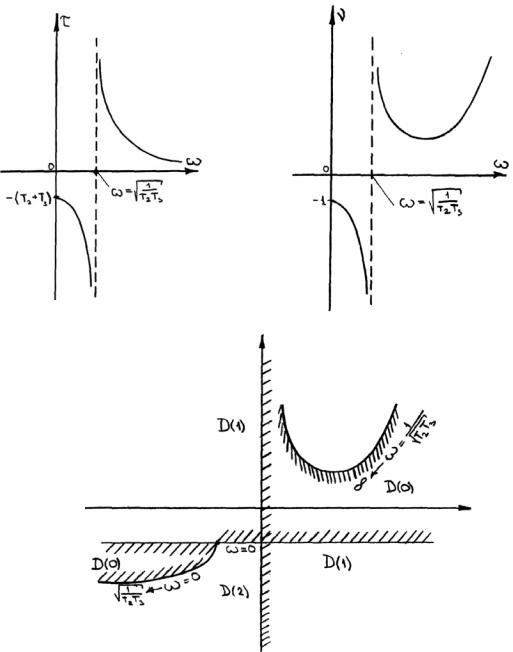
2.5.3. Для упрощения процесса можно построить вспомогательные графики τ (ω ) и ν (ω ) (рис. 3а, 3б), а затем самую границу D-разбиения (рис.3 в)

8

а)

б)

в)

Рис.3. Построение границы D-разбиения по двум параметрам; а – зависимость τ (ω ); б – зависимость ν (ω );

в – граница D-разбиения.

2.5.4. Для разметки принимается ν = 0, τ > 0 , тогда уравнение имеет

вид

А(р) = (1 + р τ )(1 + р Т2)(1 + р Т3) = 0,

9

т.е. три отрицательных корня, cистема устойчива, т.е. область Д(0) – устойчива.

2.5.5.Размечаем другие области, переходя через границы. Областей устойчивости Д (0) две.

2.5.6.При мнимых значениях коэффициента усиления (к=ν ) система

устойчива при любом τ = Т1; при больших значениях к система устойчива либо при малых Т1, либо

при достаточно больших Т1.

3.Задания для самостоятельной работы.

3.1.Для замкнутой системы управления с характеристическим уравнением

(Т1 р + 1) (0,5 р + 1) (0,05 р + 1) + 25 = 0

выделить область устойчивости по параметру Т1.

3.2.Выделить область устойчивости по параметру к для системы с характеристическим уравнением (0,5 р + 1) (0,1 р + 1) (р + 1) + к = 0.

3.3. Для системы с характеристическим уравнением

(Т1 р + 1) (Т2² р² + Т3 р + 1) + к1 кр = 0

построить область устойчивости по двум параметрам кр и Т2², если остальные параметры заданы и равны: Т1 = 0,06 с; Т3 = 0,1 с; к1 = 1.

3.4. Построить область устойчивости по параметрам Т1 и к1, если характеристическое уравнение имеет вид

(Т1 р + 1) (Т2 р + 1) (Т3 р + 1) + к1 к2 к3 = 0, где Т2 = 0,1 с; Т2 = 0,5 с; к2 к3 = 20.

10

Литература

1.Сборник задач по теории автоматичекого регулирования /Под ред. В.А.Бесекерского.- М.:Физматиз.-1963. – 409 с.

2.Теория автоматического управления. Часть 1. /Под ред. А.В.

Нетушила.-М.:ВШ.-1968.-424с.

3.Куропаткин П.В. Теория автоматического управления. – М.:ВШ.-

1973.-528с.

4. Теория автоматического управления. Часть 1. /Под ред. А.А.

Воронина.- М.:ВШ.-1986.- 362 с.

11