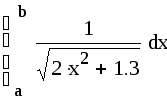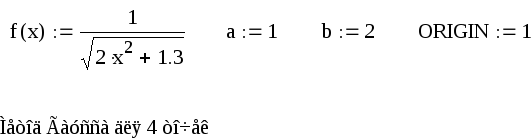ВЫЧ.МАТ. Лекции и задания / ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ12
.docЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и известна ее первообразная
и известна ее первообразная
![]() ,
то определенный интеграл от этой функции
в пределах от a
до b
может быть вычислен по формуле
Ньютона-Лейбница:
,
то определенный интеграл от этой функции
в пределах от a
до b
может быть вычислен по формуле
Ньютона-Лейбница:
![]() ,
,
где
![]() .
Однако, во многих случаях первообразная
функция не может быть найдена с помощью
элементарных средств.
.
Однако, во многих случаях первообразная
функция не может быть найдена с помощью
элементарных средств.
Данную
функцию
![]() на рассмотренном отрезке
на рассмотренном отрезке
![]() заменяют интерполирующей или
аппроксимирующей функцией
заменяют интерполирующей или
аппроксимирующей функцией
![]() простого вида (например, полином), а
затем приближенно полагают
простого вида (например, полином), а
затем приближенно полагают
![]() .
.
Функция
![]() должна быть такова, чтобы
должна быть такова, чтобы
![]() вычислялся непосредственно. Если функция
вычислялся непосредственно. Если функция
![]() задана аналитически, то ставится вопрос
об оценке погрешности формулы (2).
Рассмотрим применение в качестве
задана аналитически, то ставится вопрос
об оценке погрешности формулы (2).
Рассмотрим применение в качестве
![]() интерполяционного полинома Лагранжа.
интерполяционного полинома Лагранжа.
![]() , (1)
, (1)
где
![]() - ошибка квадратурной формулы (1) или
остаточный член
- ошибка квадратурной формулы (1) или
остаточный член
Выбрав
шаг
![]() разобьем отрезок
разобьем отрезок
![]() с
помощью равноотстоящих точек
с
помощью равноотстоящих точек
![]() ,
,
![]() ,
,
![]() на
n
равных частей, и пусть
на
n
равных частей, и пусть
![]() .
Заменяя функцию y
соответствующим интерполирующим
полиномом Лагранжа
.
Заменяя функцию y
соответствующим интерполирующим
полиномом Лагранжа
![]() ,
,
получим приближенную квадратурную формулу:
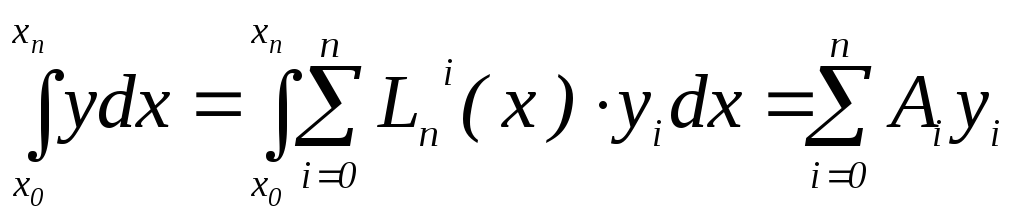 ,
(2)
,
(2)
![]() -
некоторые постоянные коэффициенты.
Найдём явные выражения для коэффициентов
-
некоторые постоянные коэффициенты.
Найдём явные выражения для коэффициентов
![]() формулы
(2).
формулы
(2).
 (3)
(3)
Коэффициенты полинома Лагранжа имеют вид:
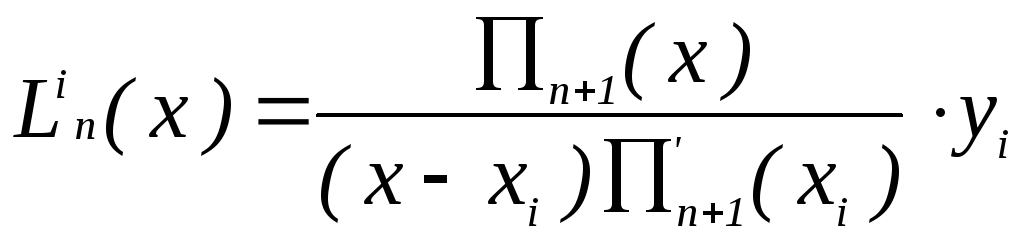 ,
(4)
,
(4)
где
![]() ,
причем
,
причем
![]() .
.
Введя
обозначения :
![]() и
и
![]() будем иметь
будем иметь
![]() ,
,
или,
т.к.
![]() ,
,
![]() ,
,
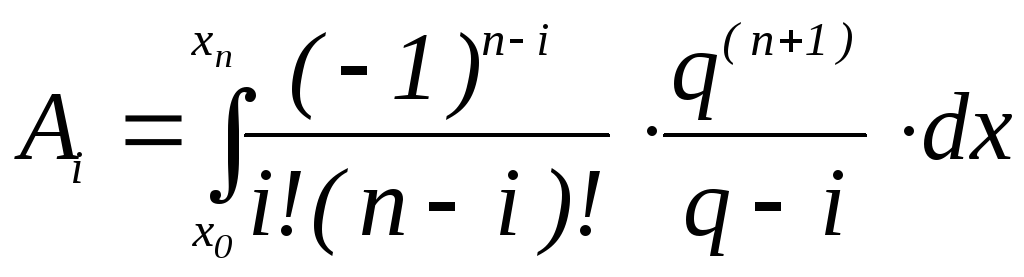 ,
то, сделав замену переменных в определенном
интеграле, будем иметь:
,
то, сделав замену переменных в определенном
интеграле, будем иметь:
![]() .
.
Т.к.
![]() ,
то обычно полагают
,
то обычно полагают
![]() ,
где
,
где
![]() - постоянные, называемые коэффициентами
Котеса.
- постоянные, называемые коэффициентами
Котеса.
Квадратурная формула (2) принимает вид:
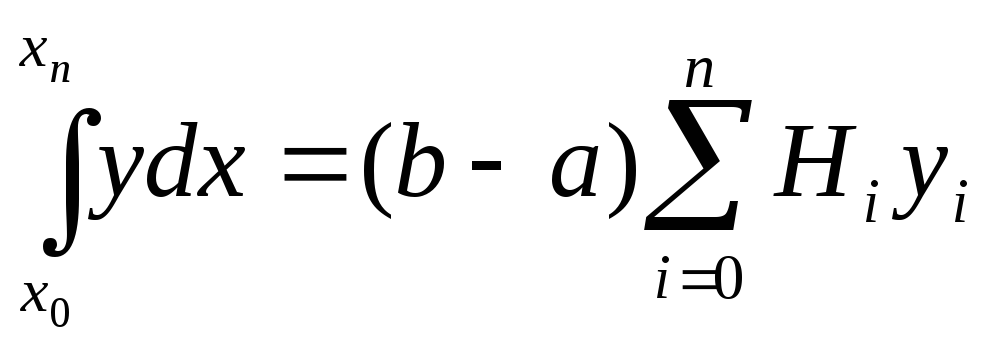 (5)
(5)
:
Такие формулы называются квадратурными формулами Ньютона-Котеса
Справедливы
соотношения: 1.
![]()
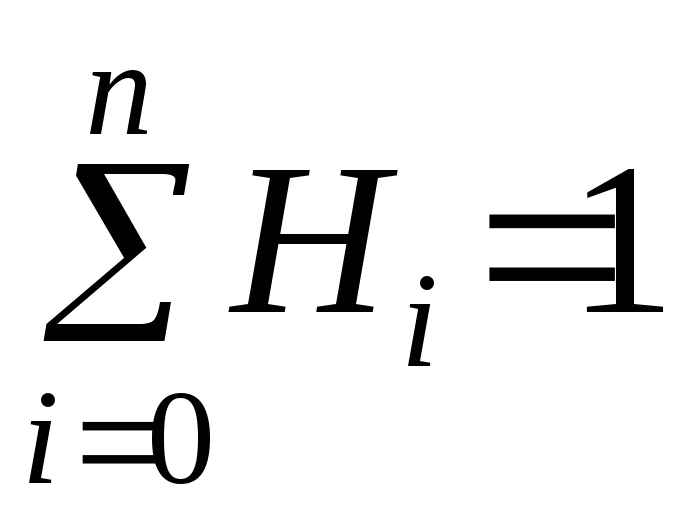 ; 2.
; 2.
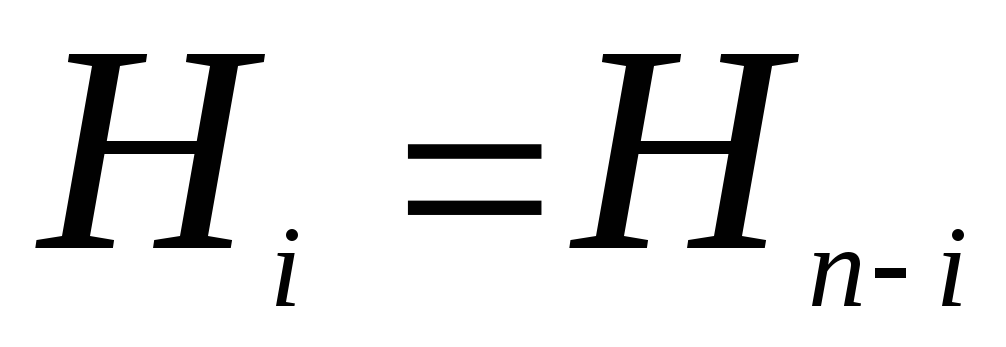 .
.
Формула трапеций и ее остаточный член
При n=1 получим
![]() ,
,
![]() :
:
отсюда
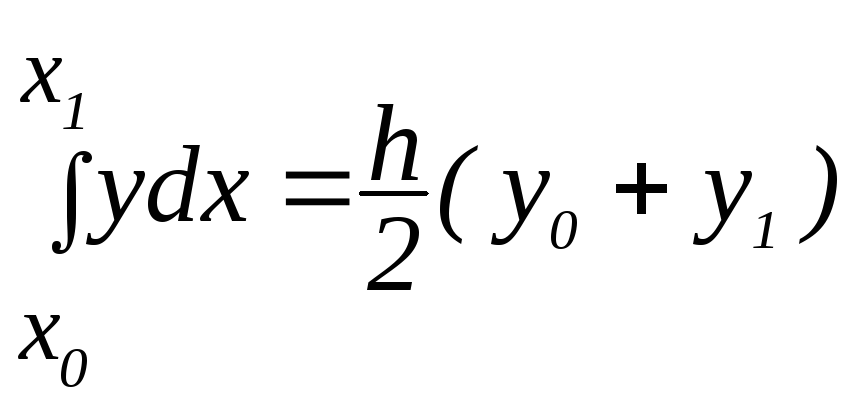 (7)
(7)
Мы
получили формулу трапеций 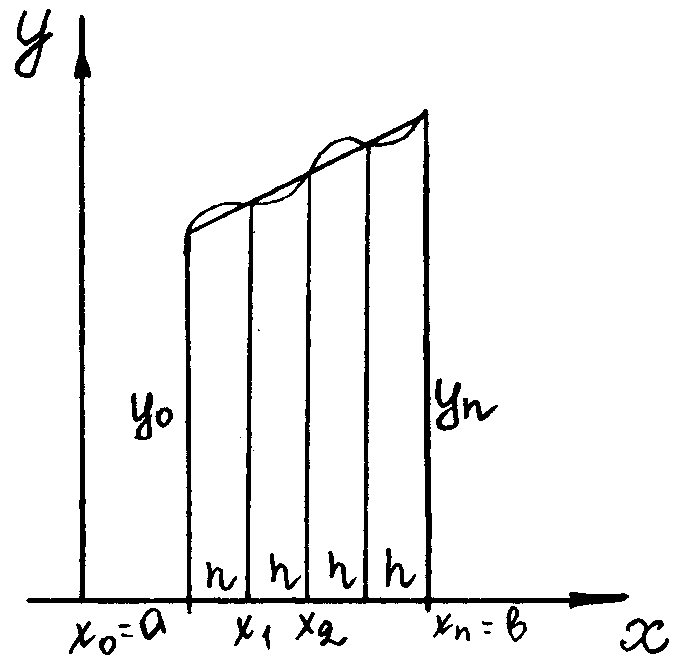 Для
вычисления интеграла
Для
вычисления интеграла
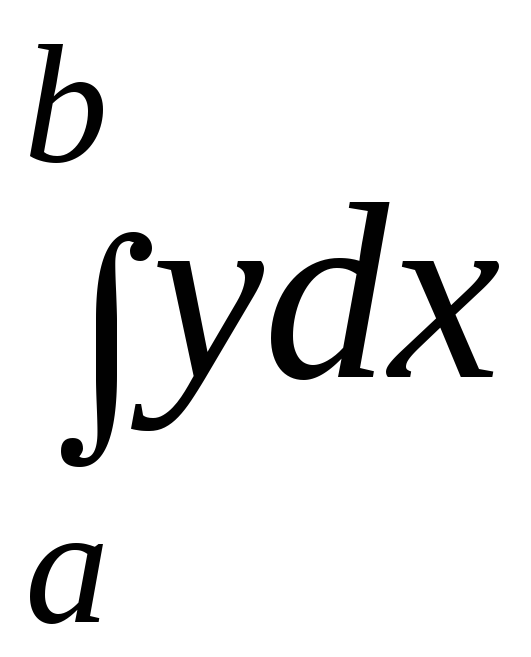 разделим промежуток интегрирования
разделим промежуток интегрирования
![]() на n
равных частей
на n
равных частей
![]() и к каждому из них применим формулу
трапеций (7). Полагая
и к каждому из них применим формулу
трапеций (7). Полагая
![]() и обозначая через
и обозначая через
![]() значения подынтегральной функции в
точках xi
будем иметь:
значения подынтегральной функции в
точках xi
будем иметь: 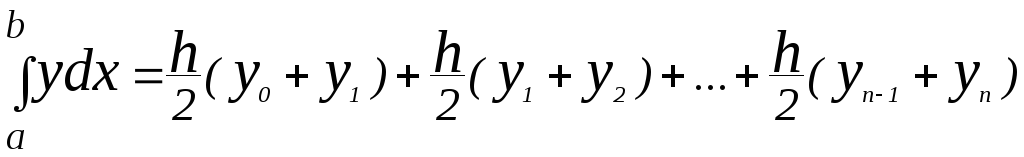 ,
или
,
или
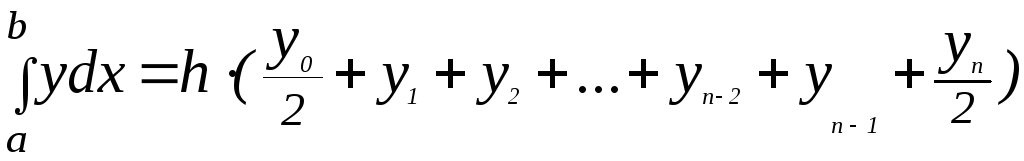 . (8)
. (8)
Геометрически
формула (1) получается в результате
замены графика подынтегральной функции
![]() ломаной линией.
ломаной линией.
Если
подынтегральная функция
![]() дважды
дифференцируема, то остаточный член
квадратурной формулы (7) равен:
дважды
дифференцируема, то остаточный член
квадратурной формулы (7) равен:
 где
где
![]() .
(9)
.
(9)
Рассмотрим
среднее арифметическое значение второй
производной
![]() на отрезке
на отрезке
![]() по всем промежуткам
по всем промежуткам
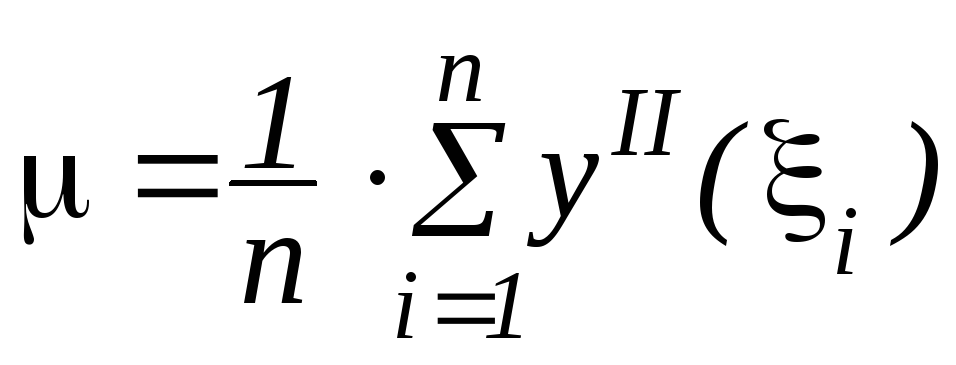 .
.
Очевидно,
заключается между наименьшим m2
и наибольшим M2
значениями второй производной
![]() на отрезке
на отрезке
![]() ,
т.е.
,
т.е.
![]() .
.
В силу
непрерывности
![]() на
отрезке
на
отрезке
![]() ,
она принимает все значения от m2
до M2. Значит
существует точка ξ, такая что
μ=f''(ξ). Из
формулы (9) получим
,
она принимает все значения от m2
до M2. Значит
существует точка ξ, такая что
μ=f''(ξ). Из
формулы (9) получим
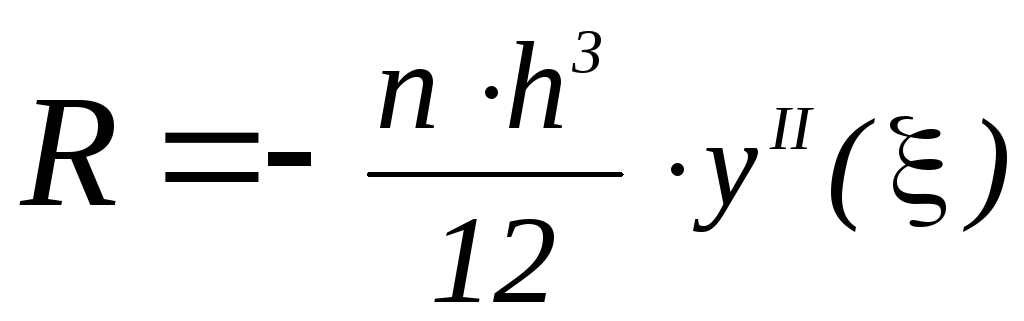 (10)
(10)
![]()
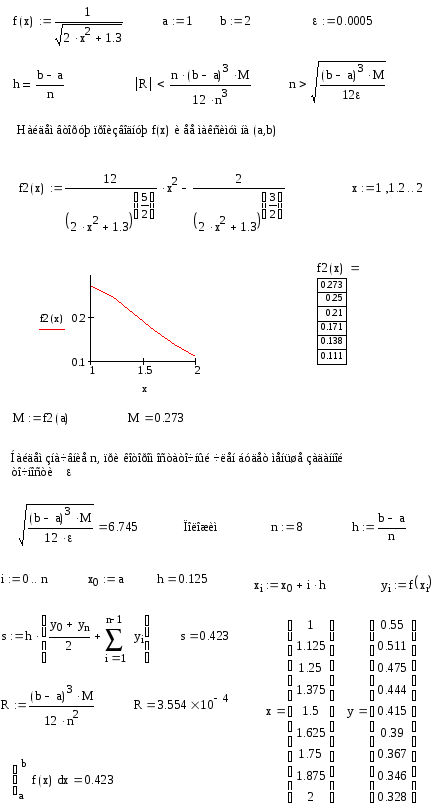
Пример выполнения в Маткаде Вычислить интеграл
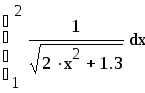
по методу трапеций с тремя десятичными знаками. В Маткаде числа могут быть вычислены с 17 десятичными знаками, поэтому не будем учитывать погрешности вычислений и тогда погрешность метода ε=0,0005 Для достижения заданной точностирешим неравенство

Ф ормула
Симпсона и ее остаточный член
ормула
Симпсона и ее остаточный член
при n=2
![]() .
.
![]() .
.
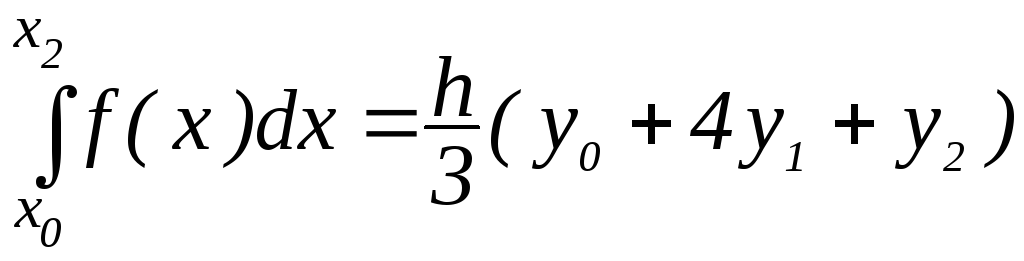 .
.
Остаточный
член: ![]() .
.
Общая формула Симпсона и ее остаточный член
Пусть
n=2m
есть четное число и
![]() - значения функции
- значения функции
![]() для равноотстоящих точек
для равноотстоящих точек
![]() с шагом
с шагом
![]() .
Применяя формулу Симпсона к каждому
удвоенному промежутку
.
Применяя формулу Симпсона к каждому
удвоенному промежутку
![]() длины 2h,
будем иметь
длины 2h,
будем иметь
 .
Следовательно,
.
Следовательно,
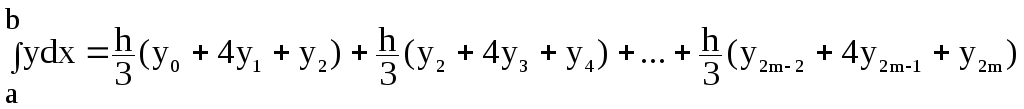 .
Отсюда получаем общую формулу Симпсона:
.
Отсюда получаем общую формулу Симпсона:
 .
.
Введя
обозначения
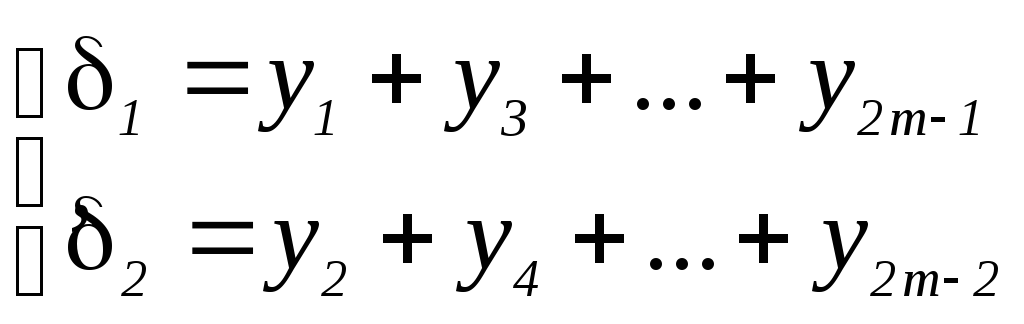 ,
формулу можно записать в более простом
виде:
,
формулу можно записать в более простом
виде:
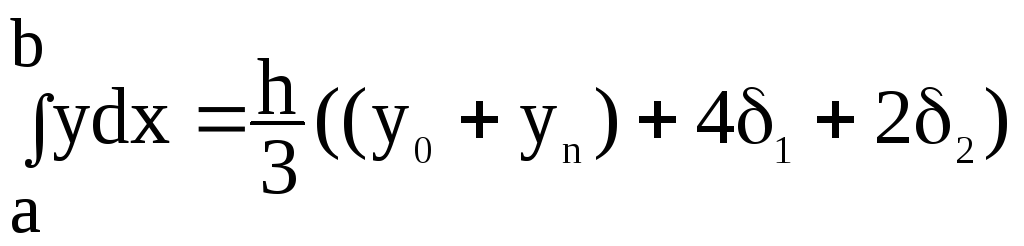 .
.
Если
функция непрерывно дифференцируема до
четвертого порядка, то ошибка формулы
Симпсона на каждом удвоенном промежутке
![]() дается формулой:
дается формулой:
![]() ,
где
,
где
![]() .
.
Суммируя все эти ошибки, получим остаточный член общей формулы Симпсона в виде:
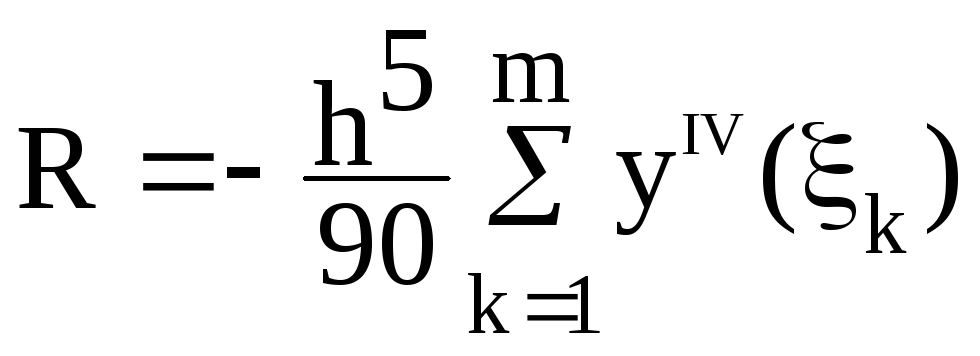 .
.
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
поэтому найдется точка
,
поэтому найдется точка
![]() такая, что
такая, что
![]() .
Следовательно
.
Следовательно
![]() (1),
(1),
где
![]() .
.
Если
задана предельная допустимая погрешность
![]() ,
то, обозначив
,
то, обозначив
![]() ,
будем иметь для определения шага h
неравенство:
,
будем иметь для определения шага h
неравенство:
![]() ,
,
отсюда
![]() ,
т.е. h
имеет порядок
,
т.е. h
имеет порядок
![]() .
Говорят, что степень точности метода
Симпсона равна четырем
.
Говорят, что степень точности метода
Симпсона равна четырем
Во многих случаях оценка погрешности квадратурной формулы весьма затруднительна. Тогда обычно применяют двойной пересчет с шагами h и 2h и считают, что совпадающие десятичные знаки принадлежат точному значению интеграла.
Предполагая,
что на отрезке
![]() производная
производная
![]() меняется медленно, в силу формулы (1)
получаем приближенное выражение для
искомой ошибки
меняется медленно, в силу формулы (1)
получаем приближенное выражение для
искомой ошибки
![]() ,
где коэффициент M
будем считать постоянным. Пусть
,
где коэффициент M
будем считать постоянным. Пусть
![]() и
и
![]() - приближенные значения интеграла
- приближенные значения интеграла
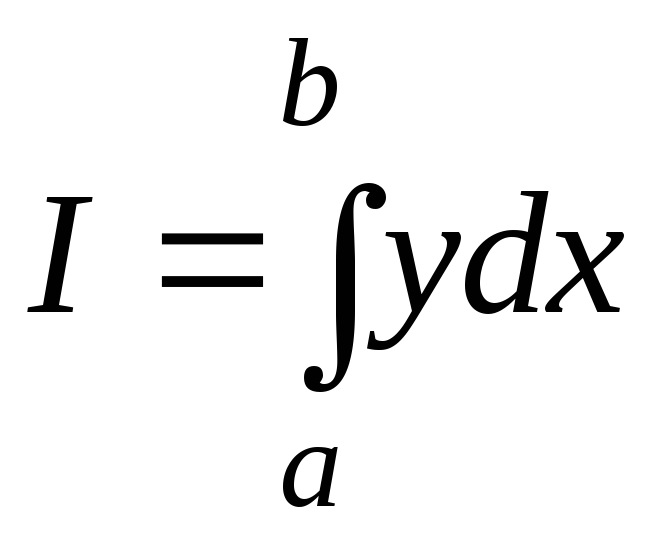 ,
полученные по формуле Симпсона
соответственно с шагом h
и H=2h.
Имеем:
,
полученные по формуле Симпсона
соответственно с шагом h
и H=2h.
Имеем:
![]() и
и
![]() .
Отсюда
.
Отсюда
![]() .
.
За приближенное значение интеграла целесообразно принять исправленное значение
![]() .
.
Пример выполнения в Маткаде Вычислить интеграл методом Симпсона для n=8. Оценить остаточный член.
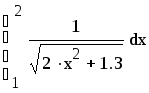
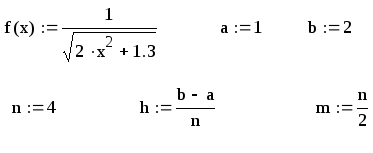

Формулы Ньютона-Котеса высших порядков:
Производя
соответствующие вычисления при n=3,
получим из
![]() квадратурную формулу Ньютона:
квадратурную формулу Ньютона:
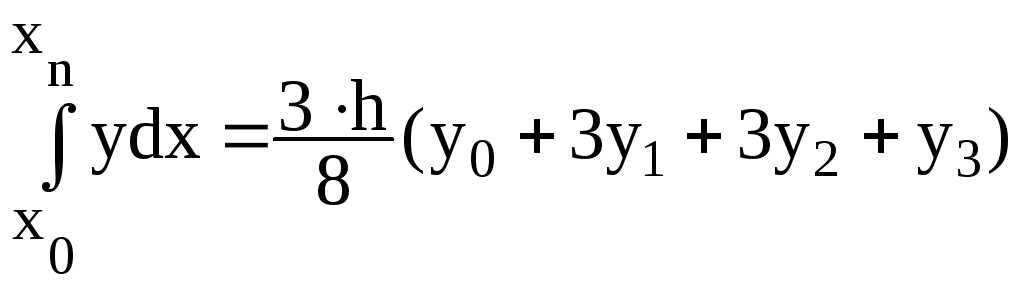 (правило
(правило
![]() ).
).
Остаточный
член формулы равен
![]() ,
где
,
где
![]() ,
т.е. при одинаковом шаге формула Ньютона,
вообще говоря, менее точна, чем формула
Симпсона.
,
т.е. при одинаковом шаге формула Ньютона,
вообще говоря, менее точна, чем формула
Симпсона.
Квадратурная формула Чебышева
Рассмотрим квадратурную формулу
![]() ,
(1)
,
(1)
где
![]() - постоянные коэффициенты. Чебышев
предположил выбрать абсциссы
- постоянные коэффициенты. Чебышев
предположил выбрать абсциссы
![]() таким образом, чтобы:
таким образом, чтобы:
-
коэффициенты
 были равны между собой;
были равны между собой; -
квадратурная формула (1) является точной для всех полиномов до степени n включительно.
Покажем,
как могут быть найдены в этом случае
величины
![]() и
и
![]() ,
полагая
,
полагая
![]() и учитывая, что при
и учитывая, что при
![]() будем иметь
будем иметь
![]() ,
отсюда получаем
,
отсюда получаем
![]() .
Следовательно, квадратурная формула
Чебышева имеет вид:
.
Следовательно, квадратурная формула
Чебышева имеет вид:
![]() .
(2)
.
(2)
Для
определения абсцисс
![]() заметим, что формула (2) согласно условию2
должна быть точной для функции вида
заметим, что формула (2) согласно условию2
должна быть точной для функции вида
![]() .
Подставляя эти функции в формулу (2),
получим систему уравнений:
.
Подставляя эти функции в формулу (2),
получим систему уравнений:
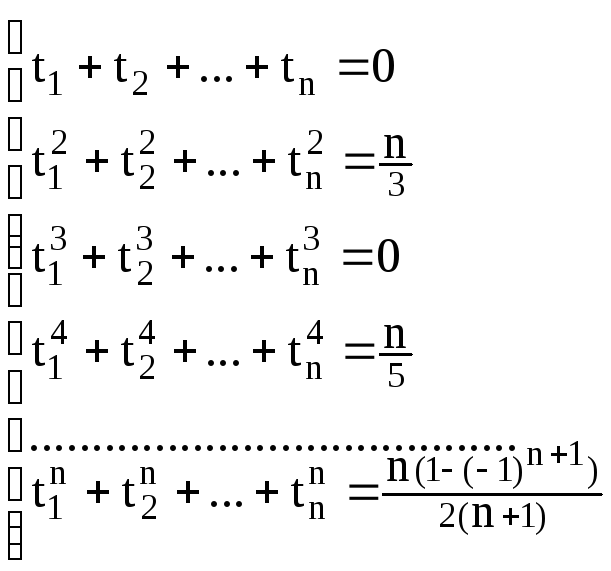 ,
(3)
,
(3)
из
которой могут быть определены неизвестные
![]() .
Заметим, что система (3) при n=8
и n10
не имеет действительных решений.
.
Заметим, что система (3) при n=8
и n10
не имеет действительных решений.
Формула Чебышева с тремя ординатами (n=3)
Для
определения абсцисс
![]() имеем систему уравнений:
имеем систему уравнений:
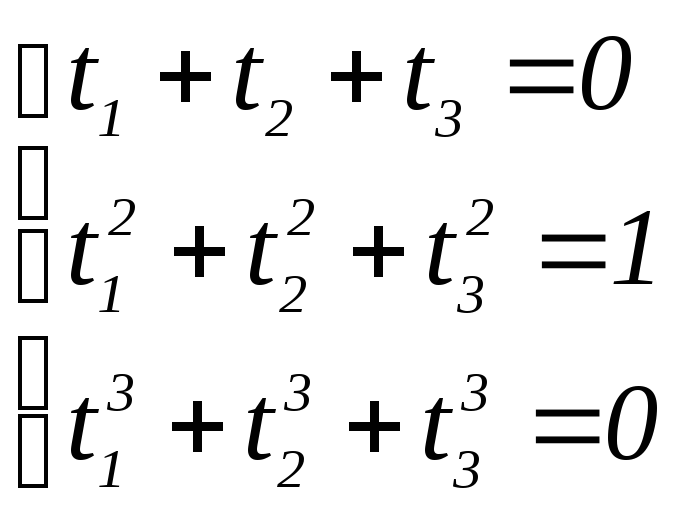 (1)
(1)
Рассмотрим
симметрические функции корней:
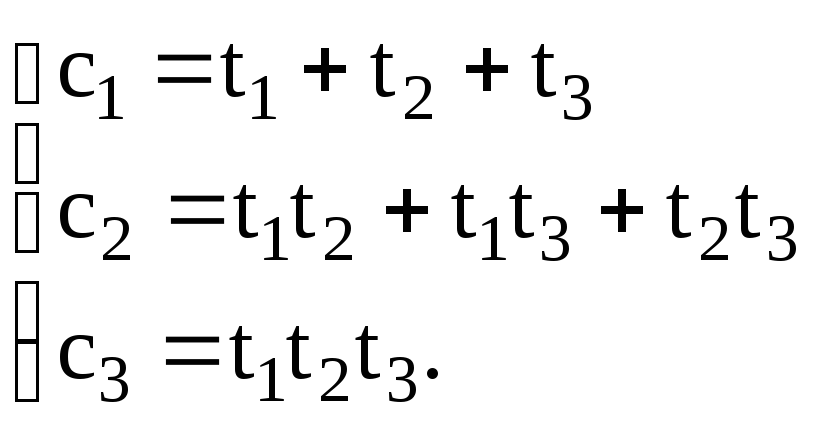
Из
системы (1) имеем:
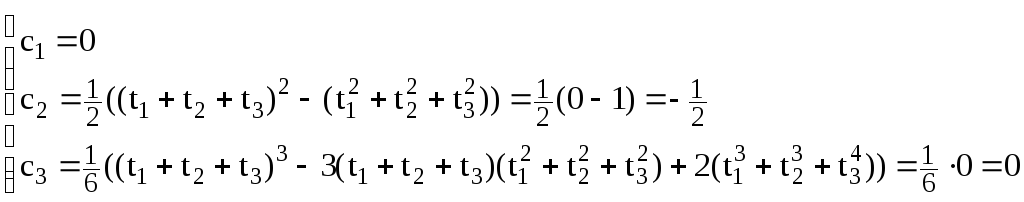
Отсюда
заключаем, что
![]() есть корни вспомогательного уравнения
есть корни вспомогательного уравнения
![]() или
или
![]() .
Следовательно, можно принять:
.
Следовательно, можно принять:
![]() .
.
Таким
образом, соответствующая формула
Чебышева имеет вид
![]() .
.
Чтобы
применить квадратурную формулу Чебышева
к интегралу вида
![]() ,
следует преобразовать его с помощью
подстановки:
,
следует преобразовать его с помощью
подстановки:
![]() ,
,
переводящей
отрезок
![]() в отрезок
в отрезок
![]() .
Применяя к преобразованному интегралу
формулу Чебышева, будем иметь
.
Применяя к преобразованному интегралу
формулу Чебышева, будем иметь
![]() ,
,
где
![]() и
и
![]() - корни системы.
- корни системы.
В таблице приведены значения корней ti системы (3) для n=1,2…,7
Значения абсцисс ti в формуле Чебышева
|
n |
i |
ti |
|
2 |
2;1 |
±0.577350 |
|
3 |
3;1 2 |
±0.707107 0 |
|
4 |
4;1 3;2 |
±0.794654 ±0.187592 |
|
5 |
5;1 4;2 3 |
±0.832498 ±0.374541 0 |
|
6 |
6;1 5;2 4;3 |
±0.866247 ±0.422519 ±0.266635 |
|
7 |
7;1 6;2 5;3 4 |
±0.883862 ±0.529657 ±0.323912 0 |
Пример выполнения в Маткаде Вычислить интеграл по формуле Чебышева для четырех и для пяти точек
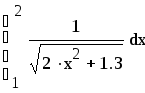
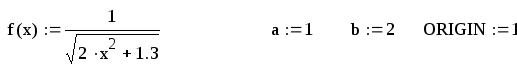


Квадратурная формула Гаусса
Полиномы
вида
![]() называются полиномами Лежандра.
называются полиномами Лежандра.
Свойства этих полиномов:
-
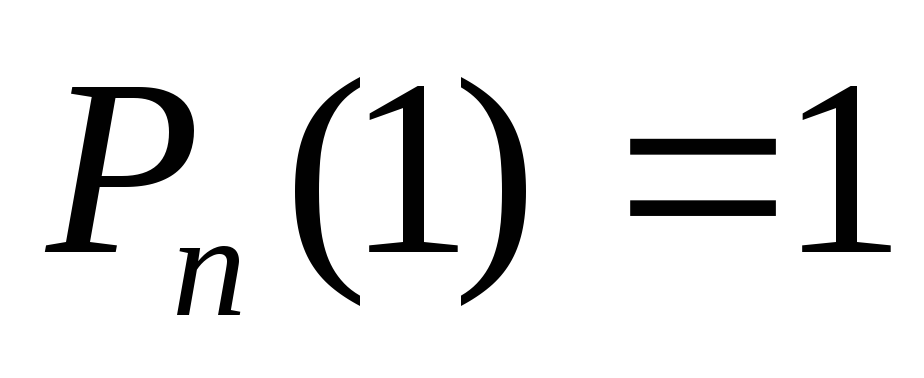 ,
,
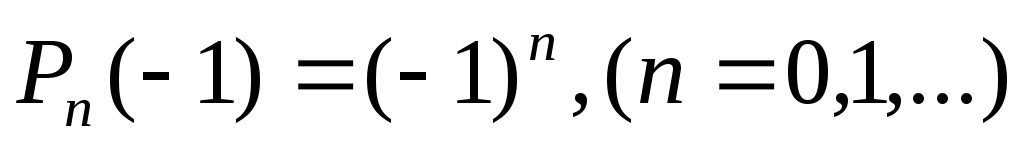 ;
; -
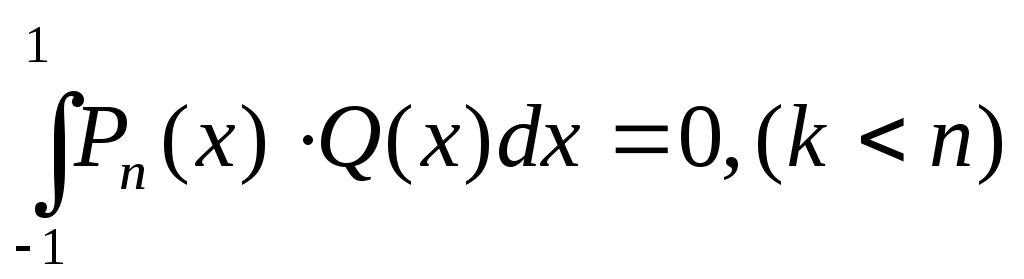 ,
где
,
где
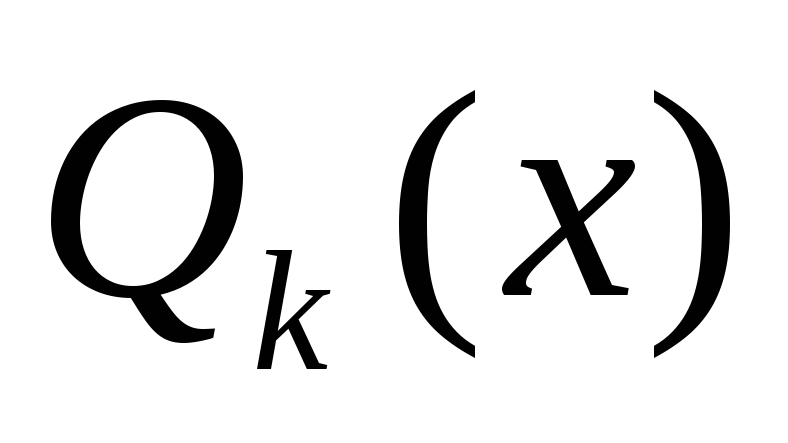 -
любой полином степени k,
меньшей n;
-
любой полином степени k,
меньшей n; -
полином Лежандра
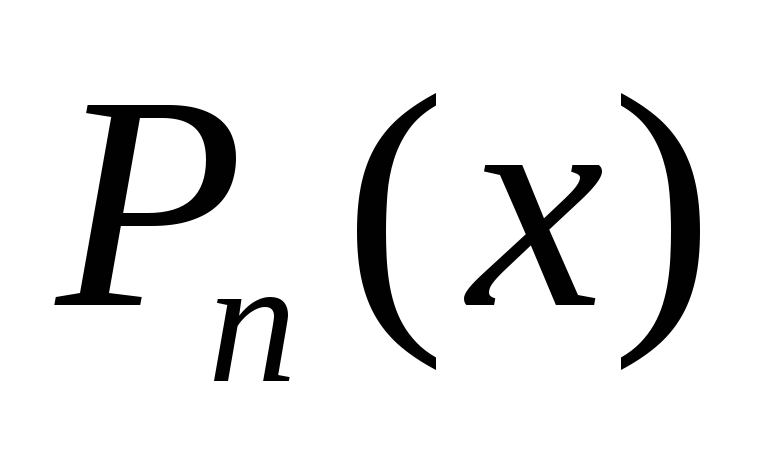 имеет n
различных и действительных корней,
которые расположены на интервале
имеет n
различных и действительных корней,
которые расположены на интервале
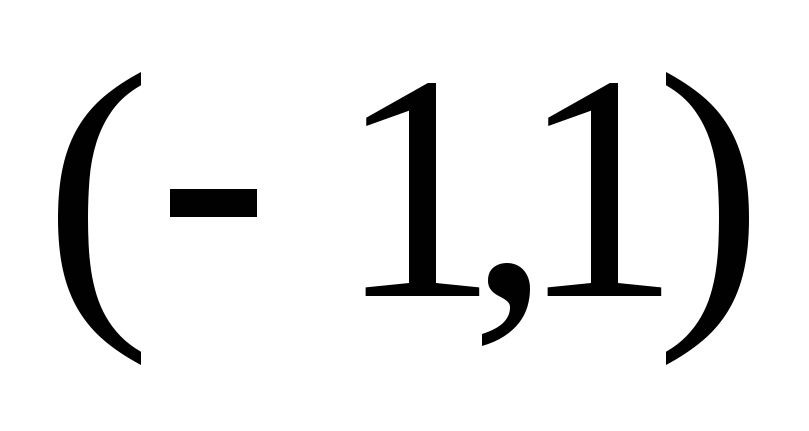 .
.
Первые
пять полиномов Лежандра:
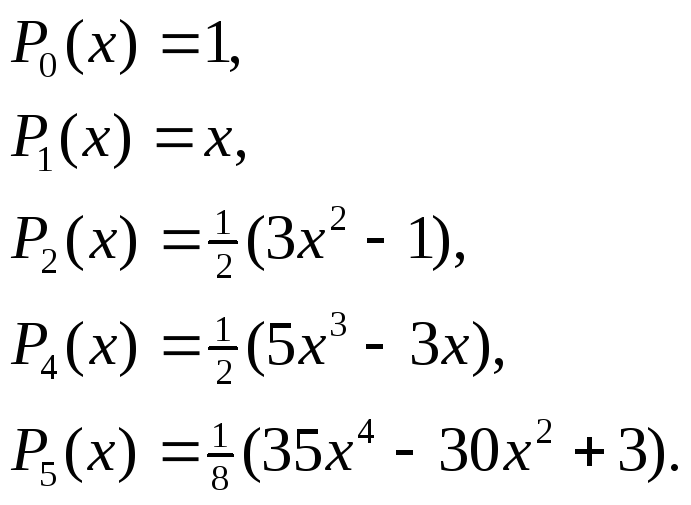
Рассмотрим
функцию
![]() ,
заданную на стандартном промежутке
,
заданную на стандартном промежутке
![]() .
Нужно подобрать точки
.
Нужно подобрать точки
![]() и коэффициенты
и коэффициенты
![]() ,
чтобы квадратурная формула
,
чтобы квадратурная формула
![]() (1)
(1)
была
точной для всех полиномов
![]() возможной наивысшей степени N.
Т.к. в нашем распоряжении имеется 2n
постоянных
возможной наивысшей степени N.
Т.к. в нашем распоряжении имеется 2n
постоянных
![]() и
и
![]() ,
а полином степени 2n-1
определяется 2n
коэффициентами, то эта наивысшая степень
в общем случае равна N=2n-1.
,
а полином степени 2n-1
определяется 2n
коэффициентами, то эта наивысшая степень
в общем случае равна N=2n-1.
Для
обеспечения равенства (1) необходимо и
достаточно, чтобы оно было верным при
![]() .
Действительно, полагая
.
Действительно, полагая
![]() и
и
![]() ,
будем иметь
,
будем иметь
![]() .
.
Таким
образом, учитывая соотношения
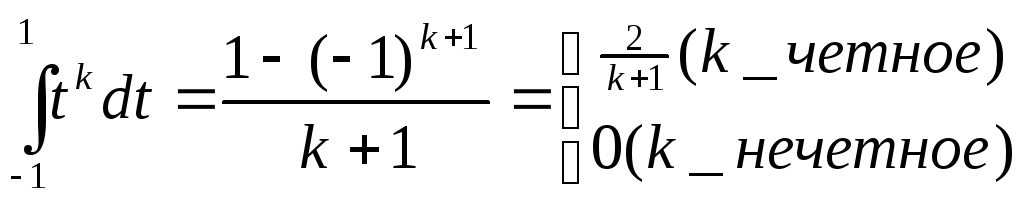 ,
заключаем, что для решения поставленной
задачи достаточно определить постоянные
,
заключаем, что для решения поставленной
задачи достаточно определить постоянные
![]() и
и
![]() из системы 2n
уравнений:
из системы 2n
уравнений:
 (3)
(3)
Система (3) нелинейная, и ее решение обычным путем представляет большие трудности.
Рассмотрим
полиномы
![]() ,
где
,
где
![]() -
полином Лежандра. Т.к. степени этих
полиномов не превышают 2n-1,
то на основании
системы (3) для них должны быть справедлива
формула (1) и
-
полином Лежандра. Т.к. степени этих
полиномов не превышают 2n-1,
то на основании
системы (3) для них должны быть справедлива
формула (1) и
![]() .
.
С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены неравенства:
![]() при
при
![]() ,
,
поэтому
![]() (4).
(4).
Равенства
(4) будут обеспечены при любых значениях
![]() ,
если положить
,
если положить
![]() ,
т.е. для достижения наивысшей точности
квадратурной формулы (1) в качестве точек
,
т.е. для достижения наивысшей точности
квадратурной формулы (1) в качестве точек
![]() достаточно взять нули соответствующего
полинома Лежандра. Как известно, из
свойства (3), эти нули действительны,
различны и расположены на интервале
достаточно взять нули соответствующего
полинома Лежандра. Как известно, из
свойства (3), эти нули действительны,
различны и расположены на интервале
![]() .
Зная абсциссы
.
Зная абсциссы
![]() ,
легко можно найти из линейной системы
первых n
уравнений определитель этой подсистемы
есть определитель Вандермонда:
,
легко можно найти из линейной системы
первых n
уравнений определитель этой подсистемы
есть определитель Вандермонда:
![]() и, следовательно,
и, следовательно,
![]() определяются однозначно.
определяются однозначно.
Формула
(1), где
![]() - нули полинома Лежандра
- нули полинома Лежандра
![]() и
и
![]() определяются из системы (3), называется
квадратурной формулой Гаусса.
определяются из системы (3), называется
квадратурной формулой Гаусса.
Рассмотрим
теперь использование квадратурной
формулы Гаусса для вычисления общего
интеграла
![]() .
Делая замену переменной
.
Делая замену переменной
![]() ,
получим
,
получим
![]() .
Применяя к последнему интегралу,
квадратурную формулу Гаусса получим:
.
Применяя к последнему интегралу,
квадратурную формулу Гаусса получим:
![]() ,
(5)
,
(5)
где
![]() ,
,
![]() - нули полинома Лежандра
- нули полинома Лежандра
![]() ,
т.е.
,
т.е.
![]() .
.
Остаточный член формулы Гаусса (5) с n узлами выражается следующим образом:
![]() .
.
Отсюда получаем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Квадратурная формула Гаусса для случая трех ординат
Полином
Лежандра третьей степени есть
![]() .
Приравнивая этот полином нулю,
находим:
.
Приравнивая этот полином нулю,
находим: ![]() ,
, ![]() ,
, ![]() .
.
Для
определения коэффициентов
![]() в силу системы (3) имеем:
в силу системы (3) имеем:

Отсюда: ![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Элементы формулы Гаусса
|
n |
t |
ti |
Ai |
|
1 |
1 |
0 |
2 |
|
2 |
1;2 |
±0.57735027 |
1 |
|
3 |
1;3 2 |
±0.77459667 0 |
0.55555556 0.88888889 |
|
4 |
4;1 3;2 |
±0.86113631 ±0.33998104 |
0.34785484 0.65214516 |
|
5 |
5;1 4;2 3 |
±0.90617985 ±0.53846931 0 |
0.23692688 0.47862868 0.56888889 |
|
6 |
6;1 5;2 4;3 |
±0.93246951 ±0.66120939 ±0.23861919 |
0.17132450 0.36076158 0.46791394 |
|
7 |
7;1 6;2 5;3 4 |
±0.94910791 ±0.74153119 ±0.40584515 0 |
0.12948496 0.27970540 0.38183006 0.41795918 |
Пример выполнения в Маткаде Вычислить интеграл по формуле Гаусса для четырех и для пяти точек.