2 Решение систем линейных алгебраических уравнений
2.1 Общие сведения
Будем рассматривать системы из n линейных уравнений с n неизвестными (2.1). Каждое слагаемое любого уравнения системы содержит только одно неизвестное, и каждое неизвестное входит только в первой степени:
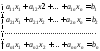(2.1).
В матричном виде эта система может быть записана так:
, (2.2),
где
.
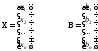Решением
системы (2.1) называется упорядоченная
совокупность чисел
,
,…,
,
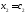которая обращает все уравнения системы
в верные равенства.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Если задана некоторая произвольная система линейных уравнений, то без предварительного исследования нельзя сказать, имеет ли она какое-либо решение, а в случае если решение существует, является ли оно единственным.
Матрица
,
полученная
из матрицы
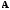добавлением столбца свободных членов,
называетсярасширенной.
Известно, что система имеет единственное
решение, если ранг матрицы
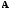равен рангу расширенной матрицы:
.
Система имеет единственное решение,
если ранг матрицы
равен числу неизвестных
,
и бесконечно много решений, если меньше
.
Если
определитель матрицы
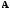не равен нулю:
,
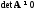то она называетсянеособенной
(невырожденной).
Система линейных алгебраических
уравнений с
неизвестными, имеющая невырожденную
матрицу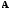
,
совместна и имеет единственное решение.
Все
эти случаи хорошо иллюстрируются
геометрически на примере системы двух
уравнений. Каждому уравнению соответствует
прямая в плоскости
,
а точка пересечения этих прямых есть
решение системы (дляn
уравнений решение есть точка пересечения
всех n
гиперплоскостей в n-мерном
пространстве).
Рис. 2.1
Если
,
то прямые имеют единственную точку
пересечения. Прямые линии, соответствующие
уравнениям системы, образуют между
собой довольно большой угол (рисунок 2.1).
Если
,
то наклоны прямых равны, и они либо
совпадают, т. е. оба уравнения изображаются
одной и той же прямой линией (рисунок 2.3),
либо параллельны (рисунок 2.2).
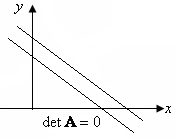
Рис. 2.2
Иногда непосредственно из поставленной задачи бывает ясно, что система уравнений не может быть вырожденной. Если же, как это бывает в большинстве случаев, соответствующая информация отсутствует, то приходится или проверять вырожденность системы уравнений в процессе решения, или исследовать такую вырожденность непосредственно.
Рис. 2.3
Непосредственная проверка состоит в вычислении определителя системы. К сожалению, вычислить определитель ничуть не легче, чем просто решить систему уравнений. При решении системы методом Гаусса проверка вырожденности системы производится автоматически в процессе решения.
С точки зрения обычной математики система линейных уравнений всегда является вырожденной, или невырожденной. С точки зрения практических вычислений могут существовать почти вырожденные системы, при решении которых получаются недостоверные значения неизвестных.
Система
двух линейных уравнений, которая является
почти вырожденной, иллюстрируется на
рискнке 2.4. Дело в том, что две прямые
линии, описываемые двумя уравнениями
системы почти параллельны. При этом
небольшое изменение наклона или сдвиг
одной прямой сильно меняет положение
точки пересечения (рисунок 2.4, пунктир).
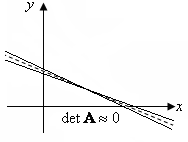
Рис. 2.4
Системы
такого типа называются плохо
обусловленными
.
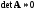В любом случае, когда две линии (либо плоскости, либо гиперплоскости) почти параллельны, система уравнений становится плохо обусловленной. В этом случае найти численное решение системы становится трудно. Более того, система из трёх и более уравнений может оказаться плохо обусловленной, даже если никакие плоскости не являются параллельными.
Представьте себе три параллельные линии, проходящие через три вершины треугольника и перпендикулярные к его плоскости. Теперь проведите плоскость через каждую пару параллельных линий. Эти плоскости не параллельны, но они нигде не пересекаются в одной точке. Если же одна из плоскостей слегка наклонена, то три плоскости пересекутся в одной точке, но система уравнений будет плохо обусловленной.
Методы численного решения системы линейных уравнений подразделяются на прямые и итерационные.
Прямые методы дают решение системы за конечное число арифметических операций. Если все операции выполнены точно, т. е. без ошибок округления, то решение заданной системы получается точным. К прямым методам относится метод Гаусса и его модификации.
Итерационные методы дают решение системы уравнений как предел последовательных приближений, вычисляемых по одной схеме (говорят, требуется бесконечное число арифметических операций, приводящих к точному решению). Иными словами, при использовании итерационного метода появляется ошибка ограничения (погрешность метода), отсутствующая в прямых методах.
Из сказанного выше не следует, что решение, полученное с помощью прямого метода, обязательно будет точнее, т. к. ошибка округления играет большую роль. При решении большой плохо обусловленной системы прямым методом ошибки округления могут привести к бессмысленным результатам. Несмотря на неизбежную ошибку ограничения, итерационный метод может оказаться наиболее удачным, т. к. при его использовании ошибки округления не накапливаются.