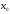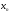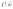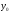3 Интерполяция

3.1 Постановка задачи

Пусть на основании эксперимента установлено, что существует функциональная зависимость между величинами и , при этом функция 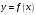остаётся нам неизвестной. Пусть значения 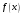образуют следующую таблицу:

Таблица 3.1

При этом требуется получить значение функции f для такого значения аргумента x, которое входит отрезок 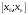, но не совпадает ни с одним из значений . В этом случае применяется особый приём: по данным значениям строят приближённую функцию 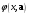, которая в некотором смысле близка к функции и аналитическим выражениям которой можно воспользоваться для вычислений, считая приближённо, что

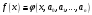(3.1)

Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и 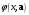в точках , то есть

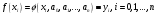, (3.2).

В этом случае нахождение приближённой функции называют интерполяцией (или интерполированием), а точки – узлами интерполяции.

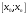Если аргумент х, для которого вычисляется приближённое значение функции, принадлежит , то задача вычисления приближённого значения функции называется интерполированием в узком смысле. Если х находится за пределами , то задача определения значения функции в точке х называется экстраполированием.

Если нелинейно зависит от параметров, то интерполяцию называют нелинейной. Мы рассмотрим линейную интерполяцию. Для линейной интерполяции наиболее удобны обычные многочлены, поскольку они легко вычисляются на ЭВМ. Другие системы функций почти не употребляются, хотя в теории подробно рассматривается интерполяция тригонометрическими многочленами и экспонентами.

Будем искать интерполирующую функцию в виде многочлена степени n:

(3.3)

Этот многочлен имеет (n+1) коэффициент. Естественно предполагать, что n+1 условия (3.2), позволит однозначно определить его коэффициенты. Действительно, требуя для выполнения условий (3.2), получаем систему (n+1) уравнений, с n+1 неизвестными:

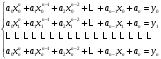(3.4).

Решая эту систему, относительно неизвестных мы и получим аналитически выражение полинома (3.3). Система (3.4) всегда имеет единственное решение, так как ее определитель, так называемый определитель Вандермонда, не равен нулю. Отсюда следует, что интерполяционный многочлен 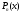для функции , заданной таблично, существует и единственный.

Этот прием можно было бы использовать для практического решения задачи, однако существуют более удобные и менее трудоемкие способы. Существуют много разных форм записи интерполяционного многочлена общего вида: Ньютона, Лагранжа, Гаусса, Грегори-Ньютона, Лапласа-Эверетта и др. Наиболее удобной для вычислений является формула Ньютона. Рассмотрим наиболее простые формы записи интерполяционных многочленов.

3.2 Интерполяционный многочлен Лагранжа

Приведем без вывода формулу интерполяционного многочлена Лагранжа, для неравноотстоящих узлов, т.е.:

. (3.5)

Эта формула называется интерполяционной формулой Лагранжа.

Запишем короче (3.6)

Построим интерполяционный многочлен Лагранжа для равноотстоящих узлов, т.е. 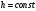(называется шагом интерполяции): .

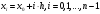Введем безразмерную независимую переменную 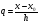тогда

, ,

……………………………………..

.

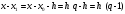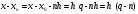Подставим эти выражения в интерполяционный многочлен (3.5) и, после несложных вычислений получим:

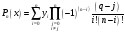(3.7).

Пример 

Построить интерполяционный многочлен Лагранжа для функции, заданной таблично:

x	1	2	4
y	3	3	9

Из таблицы видно, что степень многочлена не выше, чем 2, (единственный многочлен второй степени можно построить по трем точкам) следовательно, используем формулу квадратичной интерполяции:

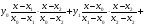
, получим: .

Если мы добавим (для данного примера) еще один узел, то интерполяционный многочлен надо составлять заново. Поэтому он неудобен для практического использования.

Непосредственное применение формулы Лагранжа приводит к большому числу однотипных вычислений, однако, составление программы не должно вызывать затруднений. Для составления программы вычисления одного значения интерполяционного многочлена Лагранжа, воспользуемся формулой (3.6).

Блок- схема алгоритма представлена на рисунке 3.1. В качестве исходных данных вводятся массивы значений 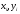и точка, в которой требуется вычислить значение функции. Отметим без доказательства, что если 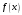имеет производную -го порядка на , то погрешность при замене функции 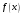многочленом 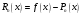удовлетворяет неравенству:

.