
Введение
В самых разнообразных областях науки и техники приходится встречаться с такими математическими задачами, для которых невозможно получить решения классическими методами или же решение может быть получено в таком сложном виде, который неприемлем для практического использования. Сложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных, таких как вычисление интегралов, решение систем линейных уравнений и т.п.
Численные методы являются одним из мощных математических средств решения задачи. Простейшие численные методы мы используют повсюду, например, извлекая квадратный корень на листке бумаги. Процесс решения задачи в общем случае включает в себя следующие этапы:
постановка задачи и построение математической модели;
разработка алгоритма;
запись алгоритма на языке программирования;
исполнение программы;
анализ полученных результатов.
Наиболее сложным этапом решения задачи является построение математической модели, которая может иметь вид уравнения, системы уравнений и т.д. Круг задач, с которыми приходится сталкиваться в вычислительной математике, очень широк. Но никакой курс не может дать окончательных рецептов для решения всех конкретных задач. Вычислительная работа требует творческого подхода, и выполнение данной курсовой работы призвано служить подспорьем, позволяющим с большей эффективностью находить пути для решения задач практики.
По курсу «Информатика», который является общеобразовательной дисциплиной, при подготовке инженеров Бийском технологическом институте, учебным планом предусмотрено выполнение курсовой работы. Ознакомление студентов с основными численными методами предполагается в рамках курсовой работы, которую студенты выполняют во втором семестре.
1 Решение нелинейного уравнения численным методом
1.1 Постановка задачи
В общем случае нелинейное уравнение можно записать в виде
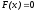 , (1.1)
, (1.1)
где функция
определена и непрерывна на конечном
или бесконечном интервале
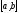 .
.
Любое число
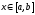 ,
обращающее функцию
,
обращающее функцию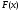 в нуль,
в нуль,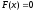 ,
называется корнем уравнения (1.1).
,
называется корнем уравнения (1.1).
Два уравнения
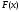 и
и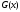 называются равносильными, если всякое
решение каждого из них, является решением
и для другого.
называются равносильными, если всякое
решение каждого из них, является решением
и для другого.
Нелинейные уравнения с одним неизвестным подразделяются на алгебраические и трансцендентные.
Уравнение (1.1)
называется алгебраическим, если функция
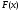 является многочленом. Известно, что
всякое алгебраическое уравнение степениnимеет ровноnкорней, вещественных или комплексных,
если каждый корень считать столько раз,
какова его кратность. Если функция
является многочленом. Известно, что
всякое алгебраическое уравнение степениnимеет ровноnкорней, вещественных или комплексных,
если каждый корень считать столько раз,
какова его кратность. Если функция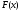 не является алгебраической, то уравнение
(1.1) называется трансцендентным. В общем
случае уравнение (1.1) может быть решено
с помощью известных формул лишь для
очень узкого класса функций. Так,
например, для алгебраических уравнений
степени выше четырех не существует
общих формул, выражающих корни этих
уравнений через их коэффициенты.
Поскольку большинство уравнений не
решается точными методами, на практике
их решают с помощью численных методов.
Если функция
не является алгебраической, то уравнение
(1.1) называется трансцендентным. В общем
случае уравнение (1.1) может быть решено
с помощью известных формул лишь для
очень узкого класса функций. Так,
например, для алгебраических уравнений
степени выше четырех не существует
общих формул, выражающих корни этих
уравнений через их коэффициенты.
Поскольку большинство уравнений не
решается точными методами, на практике
их решают с помощью численных методов.
Если функция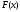 не является многочленом, то типичной
является ситуация, когда по виду уравнения
нельзя выписать точные значения корней
и даже определение числа корней
представляет трудную задачу. Решить
такое уравнение – это значит установить
имеет ли оно корни, сколько их, и найти
значения корней с заданной степенью
точности.
не является многочленом, то типичной
является ситуация, когда по виду уравнения
нельзя выписать точные значения корней
и даже определение числа корней
представляет трудную задачу. Решить
такое уравнение – это значит установить
имеет ли оно корни, сколько их, и найти
значения корней с заданной степенью
точности.
Приближенное решение уравнений, как правило, поводится в два этапа: отделение корней, т.е. нахождение достаточно малых отрезков, в которых содержится только по одному корню и уточнение корней, т.е. вычисление корней с заданной степенью точности.
Численные методы,
в которых производится последовательное,
шаг за шагом уточнение начального
приближения
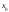 к корню, называютсяитерационными
методами, а каждый такой шаг называетсяитерацией.В результате итераций
находится последовательность приближенных
значений корня:
к корню, называютсяитерационными
методами, а каждый такой шаг называетсяитерацией.В результате итераций
находится последовательность приближенных
значений корня: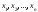 ,
называемойитерационной последовательностью.
Если с ростомnэти
значения приближаются к истинному
значению корня, то говорят, что итерационный
процесс сходится, в противном случае -
расходится. Наиболее распространенными
численными методами решения уравнения
(1.1) являются: метод хорд, метод касательных
(Ньютона), метод простой итерации и метод
половинного деления. Применение того
или иного метода для решения уравнения,
зависит от поведения функции
,
называемойитерационной последовательностью.
Если с ростомnэти
значения приближаются к истинному
значению корня, то говорят, что итерационный
процесс сходится, в противном случае -
расходится. Наиболее распространенными
численными методами решения уравнения
(1.1) являются: метод хорд, метод касательных
(Ньютона), метод простой итерации и метод
половинного деления. Применение того
или иного метода для решения уравнения,
зависит от поведения функции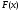 ,
числа корней и начального приближения.
,
числа корней и начального приближения.
