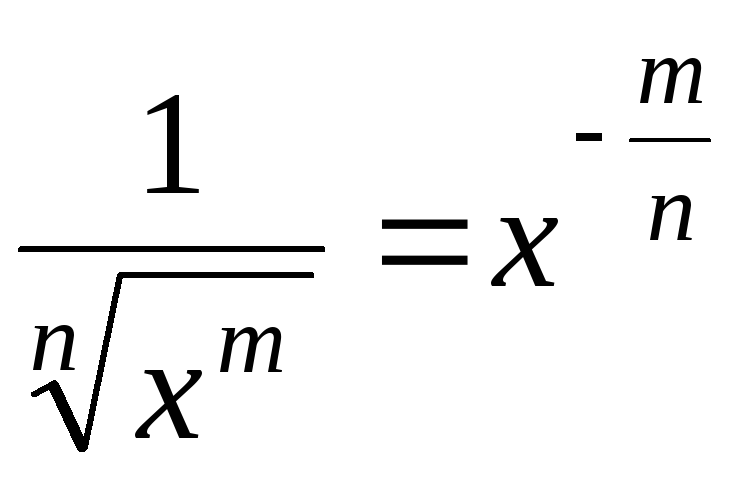- •Тема 4. Неопределенный интеграл Введение
- •Свойства неопределенного интеграла
- •Занятие №1. Непосредственное интегрирование функций
- •Ход занятия Краткая информация о новых учебных элементах
- •Геометрическая иллюстрация неопределенного интеграла
- •Задание для самостоятельной работы
- •Занятие №2. Метод замены переменных
- •Краткая информация о новых учебных элементах
- •Задание для студентов
- •Задание для самостоятельной работы
- •Занятие №3. Метод интегрирования по частям
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
- •Задание для самостоятельной работы
- •Занятие №6. Интегрирование рациональных дробей (продолжение)
- •Алгоритм нахождения интеграла методом неопределенных коэффициентов
- •Задача 6. Найти интегралы методом неопределенных коэффициентов:
- •Задание для самостоятельной работы
- •Краткая информация о новых учебных элементах
- •Задание для самостоятельной работы
Тема 4. Неопределенный интеграл Введение
В теме «Неопределенный интеграл» рассматривается задача, обратная задаче о дифференцировании функций.
Задача
состоит в следующем: дана функция
![]() ,
являющаяся производной некоторой
функции
,
являющаяся производной некоторой
функции![]() ;
требуется найти функцию
;
требуется найти функцию![]() .
.
К такой математической задаче приводят многие физические, химические и другие задачи, например, задача об отыскании закона равномерного движения материальной точки вдоль прямой по заданной скорости, задача о нахождении закона химической реакции по известной её скорости.
Особое значение эта тема имеет при решении дифференциальных уравнений, описывающих различные физические и механические процессы.
Для успешного усвоения навыков интегрирования надо, прежде всего, выучить наизусть таблицу интегралов и свойства интегралов.
Свойства неопределенного интеграла
(Правила интегрирования)
![]() (1)
(1)
![]() (2)
(2)
![]() ,
следствие:
,
следствие:
![]() (3)
(3)
![]() ,
где
,
где
![]() (4)
(4)
![]() (5)
(5)
![]() ,
если
,
если
![]() ,
то
,
то![]() (6)
(6)
ТАБЛИЦА ИНТЕГРАЛОВ
В
этой таблице использовано свойство
инвариантности формы полного дифференциала
![]() ,
откуда
,
откуда
![]() .
.
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19) |
При
использовании формул этой таблицы для
преобразования подынтегрального
выражения к виду
![]() применяются простейшие преобразования
дифференциалов:
применяются простейшие преобразования
дифференциалов:
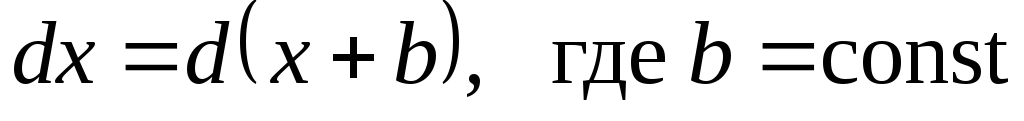 ;
;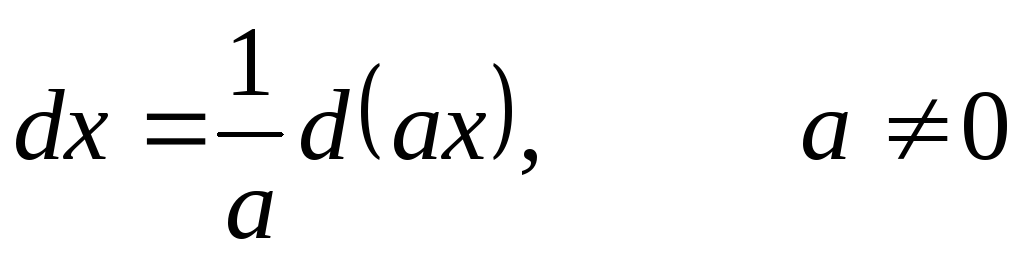 ;
;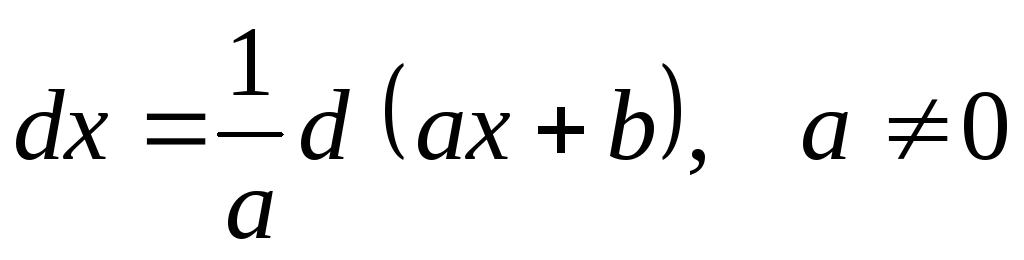 ;
;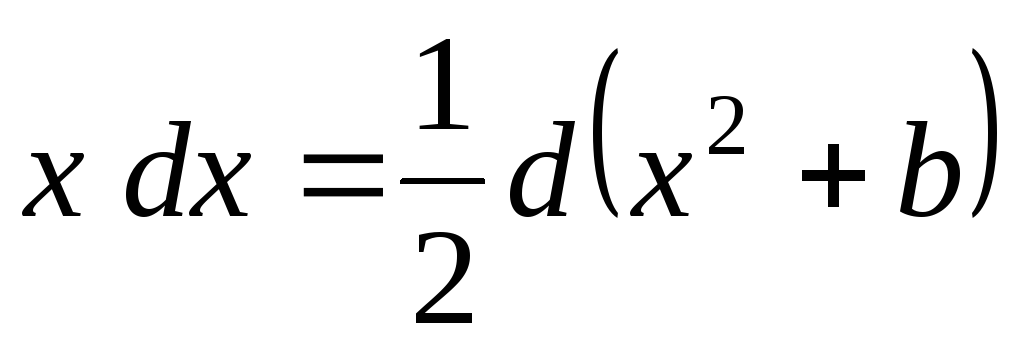 ;
;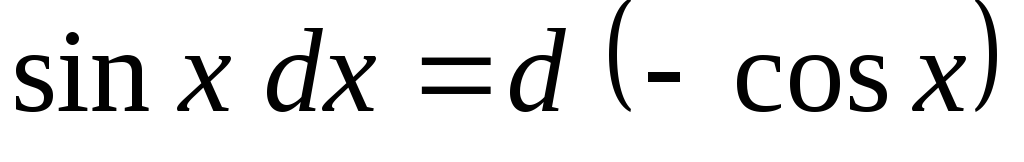 ;
; ;
;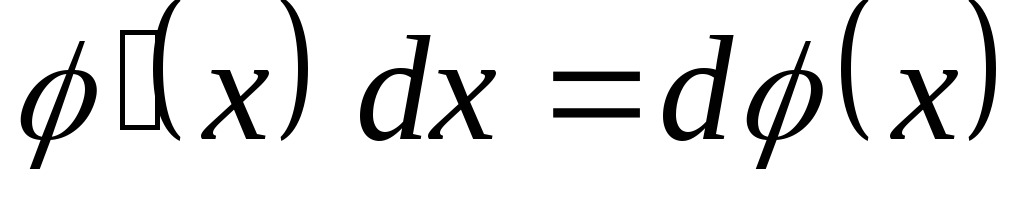 .
.
Например,
![]() .
.
Используя преобразования дифференциала можно дополнить свойства неопределенного интеграла:
Если
![]() тоа)
тоа)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Занятие №1. Непосредственное интегрирование функций
Цель занятия: усвоить новые учебные элементы на уровне знаний и умения применять их к решению типовых задач.
Учебные вопросы
1. Непосредственное интегрирование.
Ход занятия Краткая информация о новых учебных элементах
Функция
![]() называетсяпервообразной
для функции
называетсяпервообразной
для функции
![]() ,
если
,
если![]() или
или![]() .
.
Если
функция
![]() имеет первообразную
имеет первообразную![]() ,
то она имеет бесконечное множество
первообразных для
,
то она имеет бесконечное множество
первообразных для![]() ,
причем это множество задается формулой
,
причем это множество задается формулой![]()
![]() ,
где
,
где![]() постоянная.
постоянная.
Неопределенный
интеграл от функции
![]() совокупность
всех ее первообразных. Обозначение:
совокупность
всех ее первообразных. Обозначение:
![]() .
.
Здесь: ![]() знак
интеграла;
знак
интеграла;
![]() подынтегральная
функция;
подынтегральная
функция;
![]() подынтегральное
выражение;
подынтегральное
выражение;
![]() переменная
интегрирования.
переменная
интегрирования.
Отыскание неопределенного интеграла называется интегрированием функции.
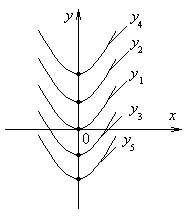
Геометрическая иллюстрация неопределенного интеграла
![]() геометрически
представляет множество интегральных
кривых вида
геометрически
представляет множество интегральных
кривых вида
![]() ,
отличающихся друг от друга постоянным
слагаемымс
(рис. 1).
,
отличающихся друг от друга постоянным
слагаемымс
(рис. 1).
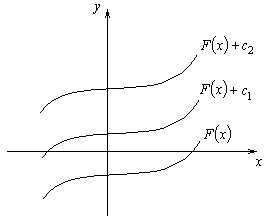
Рис. 1
Задача 1. В следующих равенствах заполнить пропущенные места по соображению:
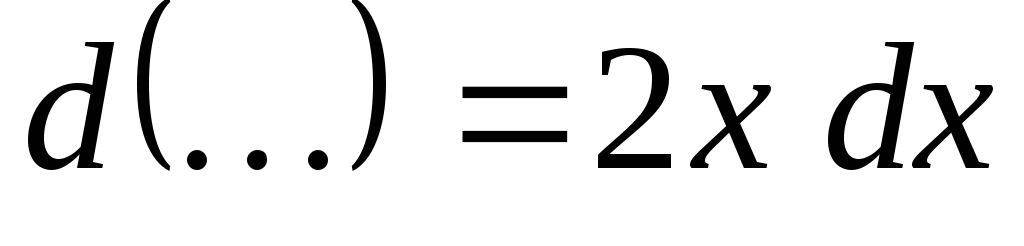 ;
;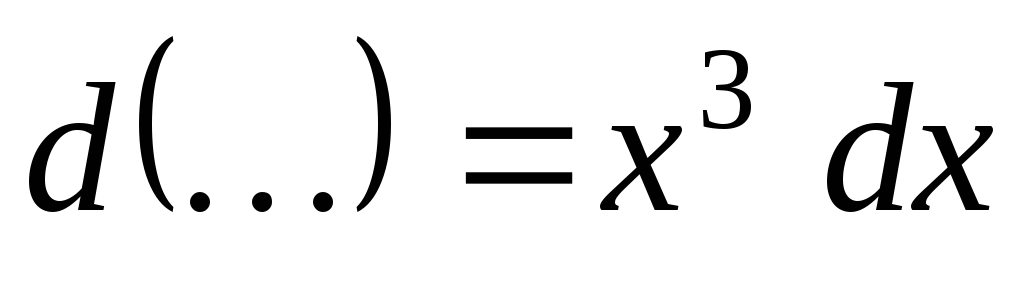 ;
;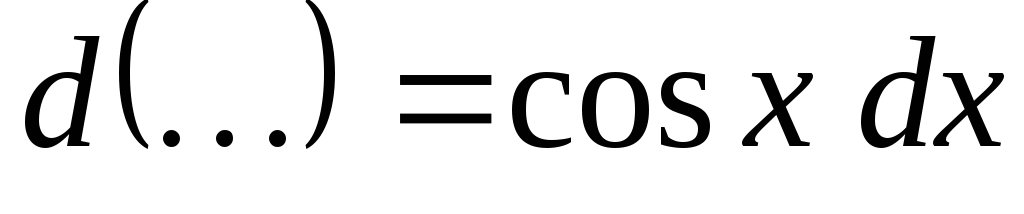 ;
;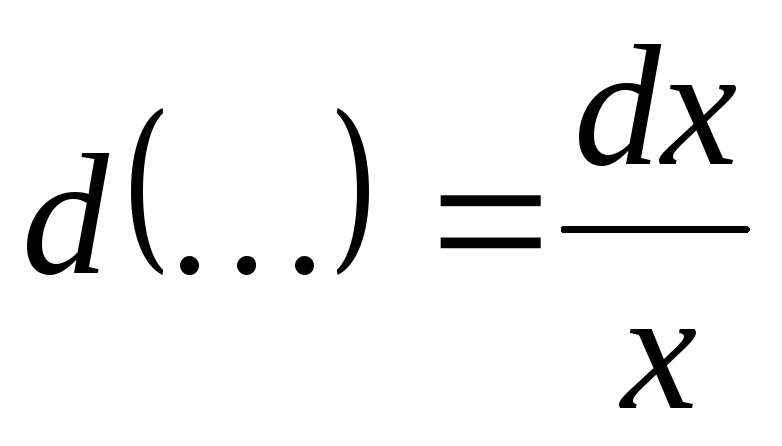 ;
;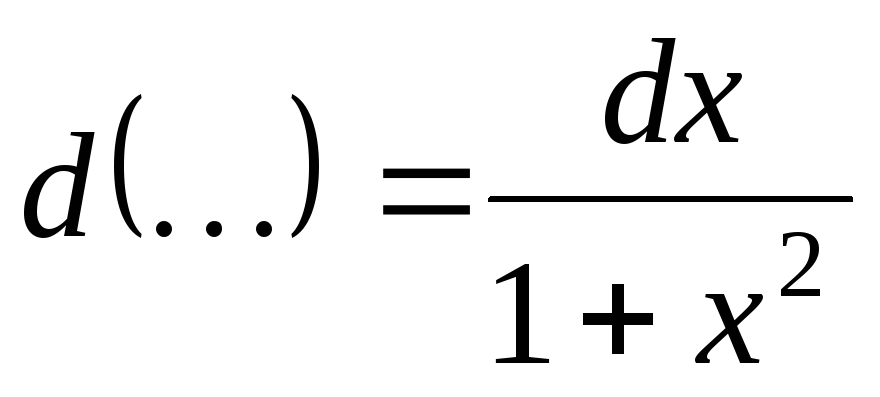 ;
;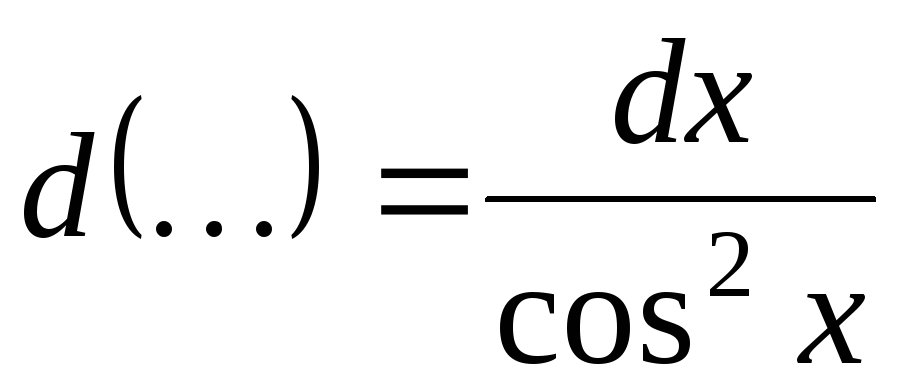 .
.
Найти
затем интегралы
![]() и т.д.
и т.д.
Построить интегральные кривые для пунктов 1 и 2.
Решение. Рассмотрим выполнение 1 пункта:
![]() ;
;
![]() .
.
Замечание.
Интеграл
![]() находится по формуле(2)
(Таблицы интегралов - Т.И.) как интеграл
степенной функции. Зная, что
находится по формуле(2)
(Таблицы интегралов - Т.И.) как интеграл
степенной функции. Зная, что
![]() ,
т.е. в данном случае
,
т.е. в данном случае![]() .
.
Интегральные
кривые: ![]() ,
где
,
где![]() ;…
(рис. 2).
;…
(рис. 2).
|
Рис. 2 |
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
Остальные пункты задачи выполняются аналогично.
Задача
2. Найти
интеграл: ![]() .
.
Решение. 1. Используя свойство (5), распишем интеграл алгебраической суммы нескольких слагаемых в виде суммы интегралов от каждого слагаемого:
![]() .
.
2. По свойству (4) во втором слагаемом постоянный коэффициент 3 вынесем за знак интеграла. Используем формулы (2), (3) (Т.И.).
![]()
![]() .
.
Задача 3. Найти интеграл:
![]() .
.
Замечание.
Если подынтегральные функции содержат
выражения вида
![]() ,
то данные интегралы находятся по формуле(2)
(Т.И.) как интегралы от степенных функций.
Прежде чем применить формулу (2),
необходимо произвести преобразования
подынтегральных функций. Для этого
воспользуемся следующими свойствами:
,
то данные интегралы находятся по формуле(2)
(Т.И.) как интегралы от степенных функций.
Прежде чем применить формулу (2),
необходимо произвести преобразования
подынтегральных функций. Для этого
воспользуемся следующими свойствами:
|
|
(1) |
Пример: |
по свойству (1) |
|
|
|
(2) |
|
по свойству (2) |
|
|
|
(3) |
|
|
|
Решение.
![]()
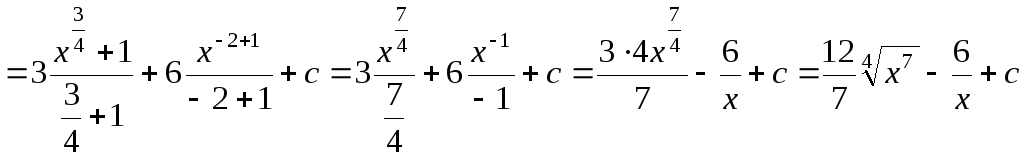 .
.
Задача 4. Найти интегралы:
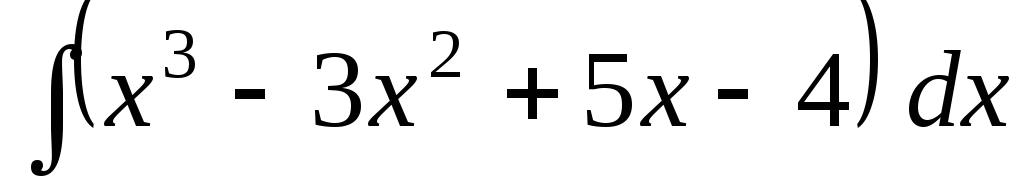 ;
; .
.
Указание. Выполнить по образцу задачи 3, используя свойства (5), (4) и формулы (1), (2), (3) (Т.И.).
Задача
5. Найти
интеграл: ![]() .
.
Замечание. Для нахождения интеграла следует разделить многочлен, стоящий в числителе, на знаменатель. Далее, произведя соответствующие преобразования (см. задачу 3), воспользоваться свойствами (4), (5) и формулой (2) (Т.И.).
Решение.
![]()
![]()
![]() .
.
Задача 6. Найти интеграл (выполнить по образцу задачи 5):
![]() .
.
Задача 7. Найти интегралы:
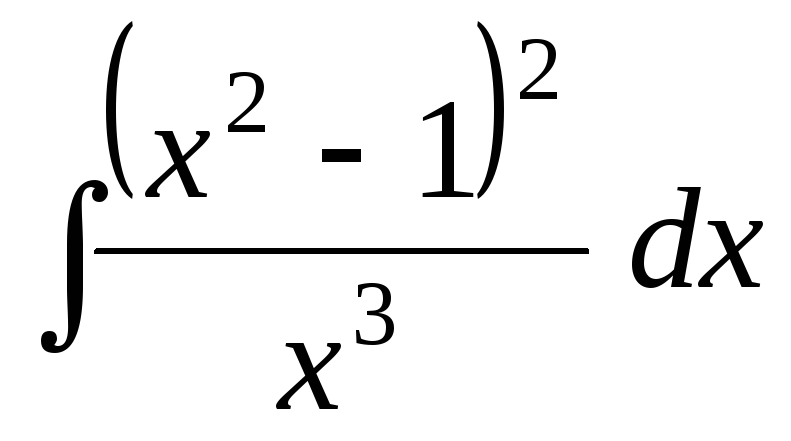 ;
;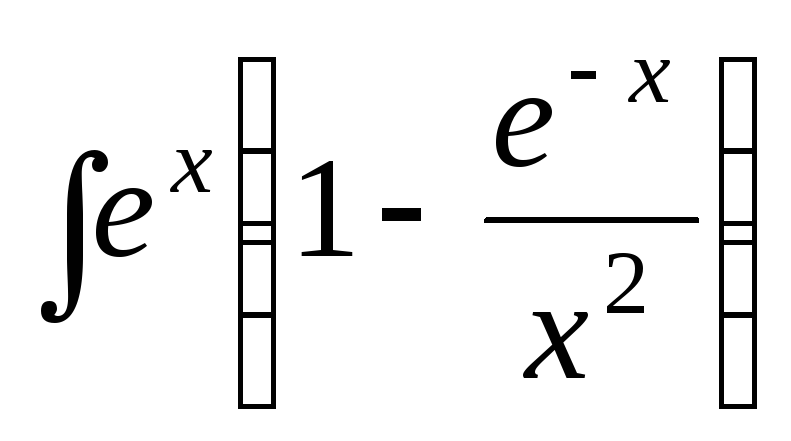
 .
.
Указание. В первом интеграле числитель возвести в квадрат, полученный многочлен разделить на знаменатель и после этого проинтегрировать. Во втором интеграле открыть скобки, сделать преобразования, после чего выполнить интегрирование.
Задача
8. Найти
интеграл: ![]() .
.
Решение. Иногда, с целью сведения подынтегральной функции к табличному интегралу, используют так называемый искусственный прием (прибавляют и вычитают одно и то же число в числителе с целью создания слагаемого, кратного знаменателю).
В данном случае в числителе прибавляют и вычитают 1.
![]() выражение
не изменилось, но теперь можно преобразовать
подынтегральную функцию:
выражение
не изменилось, но теперь можно преобразовать
подынтегральную функцию:
![]() .
.
Теперь проинтегрируем полученное выражение:
![]()
![]() .
.