Образец КР по ТВ и МС 2010(1)

Образец выполнения контрольной работы

Пусть M=0, N=10, тогда m=5, n=2.

Задача 1. В урне находятся =7 белых и =4 черных шара. Последовательно извлекаются наудачу три шара без их возвращения в урну. Найти вероятность того, что третий по счету шар окажется белым.

Решение: Пусть событие А – третий шар окажется белым.

В урне всего 11 шаров (7-белых и 4- черных).

Событие «б»- вынули белый шар.

событие «ч»- вынули черный шар.

Тогда событие А: б.б.б., либо б.ч.б., либо ч.б.б., либо ч.ч.б. Применив теоремы о сумме вероятности несовместных событий и вероятности совместного появления зависимых событий, имеем:

.

Ответ: Р(А)=0,636.

Задача 2. В урне находятся 2 шара белого цвета и =3 шара черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных трех шаров окажется:

а) ровно один белый шар;

б) не менее одного белого шара;

в) не более одного белого шара.

Решение: Пусть событие А – вынули белый шар.

В урне всего 5 шаров (2-белых и 3-черных). Т.к. каждый раз шар возвращают, то имеем повторные независимые испытания с одинаковой вероятностью «извлечь белый шар» , тогда .

а) Вероятность того, что среди трех извлеченных шаров окажется ровно один белый шар, найдем по формуле Бернулли:

.

б) Вероятность того, что среди извлеченных шаров окажется не менее одного белого шара, равна: .

в) Вероятность того, что среди извлеченных шаров окажется не более одного белого шара, равна:

.

Ответ: а) ; б); .

Задача 3. В ящике находятся =8 одинаковых пар перчаток черного цвета и =4 одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

Решение: Пусть событие А – перчатки одного цвета, причем из них одна – левая, другая – правая. Вероятность события А найдем по формуле:

1) Найдем общее количество элементарных исходов n.

Всего 12 пар перчаток; из них берут 2 перчатки. Т.к. всего перчаток 12*2=24, то общее количество элементарных исходов равно:.

2) Найдем общее количество благоприятных исходов m.

Благоприятные исходы состоят в том, что либо обе перчатки черные, при этом одна левая, другая правая; либо обе бежевые, при этом одна левая, другая правая. Используя определения суммы и произведения событий, получим:

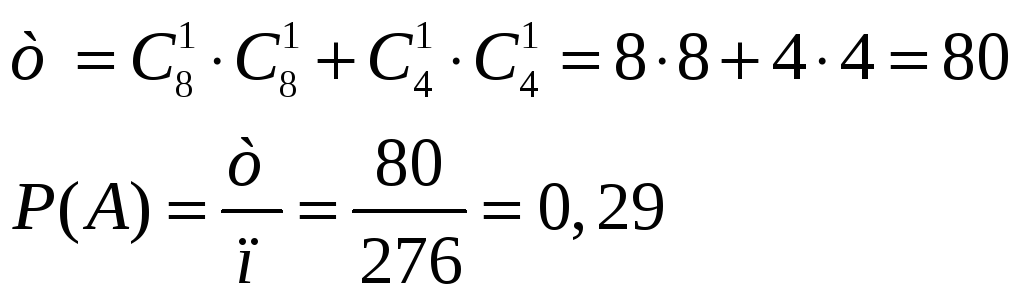Ответ: Р (А)=0,29

Задача 4. Число деталей, выпущенных на первом заводе, относится к числу деталей, выпущенных на втором заводе как . Вероятность выпуска годной детали на первом заводе равна =0,06, а для второго завода эта вероятность равна =0,5. Все детали поступают на один склад. Какова вероятность того, что наугад взятая со склада деталь будет годной?

Решение: Пусть событие А – наугад взятая со склада деталь – годная,

событие (гипотеза)детали с 1 завода, событие (гипотеза)детали с 2 завода.

Всего 6+8=14 частей. Тогда вероятности гипотез:

.

Найдем вероятность события А в каждой из гипотез: .

По формуле полной вероятности имеем:

.

Ответ: Р(А)=0,311.

Задача 5. Среди учебников =50 % старых. Вероятность того, что в старом учебнике есть все темы лекционного курса, равна 0,8. В новых учебниках отражены все темы лекционного курса с вероятностью =0,52. Учебник содержит все темы лекционного курса. Какова вероятность того, что этот учебник новый?

Решение: Пусть событие А – учебник содержит все темы.

событие (гипотеза)учебник старый, событие (гипотеза) учебник новый.

Так как старых учебников -50%, то вероятности гипотез:

.

Вероятность события А в каждой из гипотез:

.

По формуле Байеса имеем:

Ответ: Р(H₂/A)=0,394

Задача 6. Закон распределения дискретной случайной величины имеет вид:

			0
	0,2	0,1	0,2

а) Найти: вероятности , дисперсию , если математическое ожидание .

б) Построить: многоугольник распределений и функцию распределения .

Решение: а)

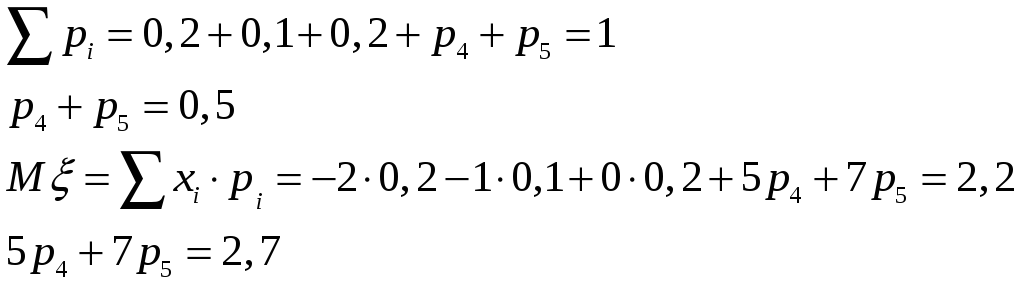
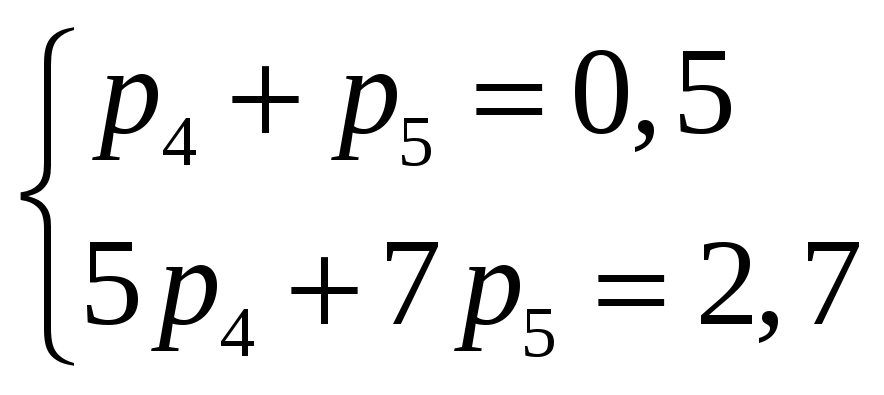
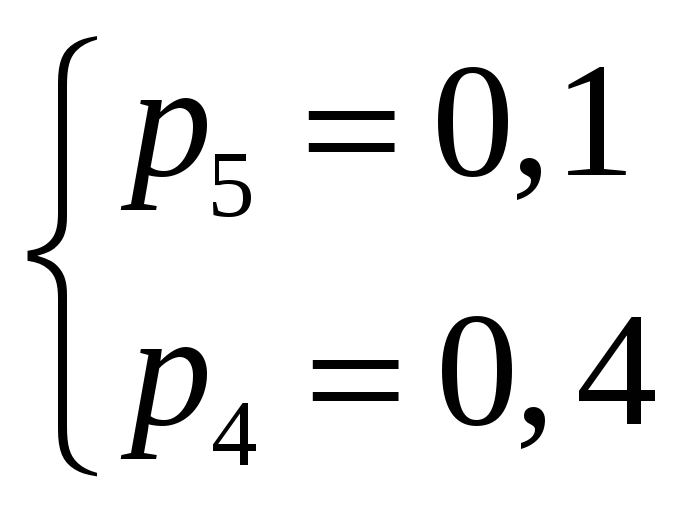
Ответ: .

Задача 7. Плотность распределения непрерывной случайной величины Х имеет вид:

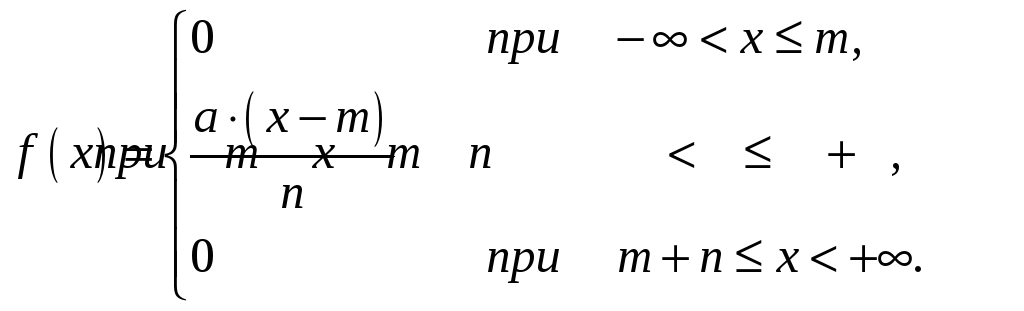
Найти: а) параметр ;

б) функцию распределения ;

в) вероятность попадания случайной величины Х в интервал ;

г) математическое ожидание M (X) и дисперсию D (X).

д) построить графики функций f(x) и F(x).

Решение:

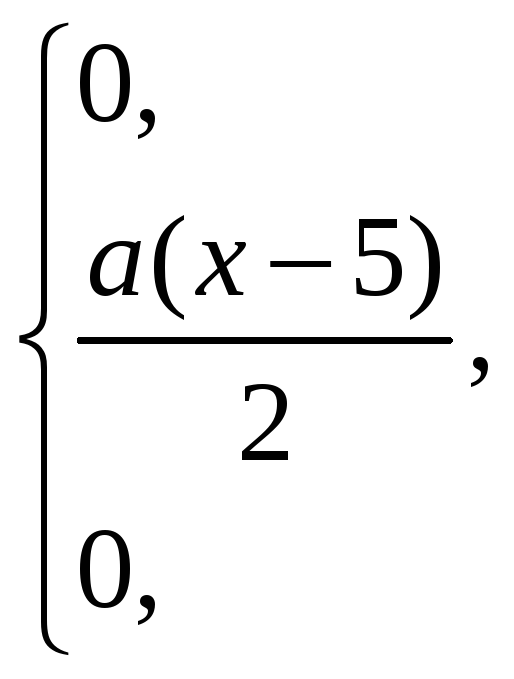
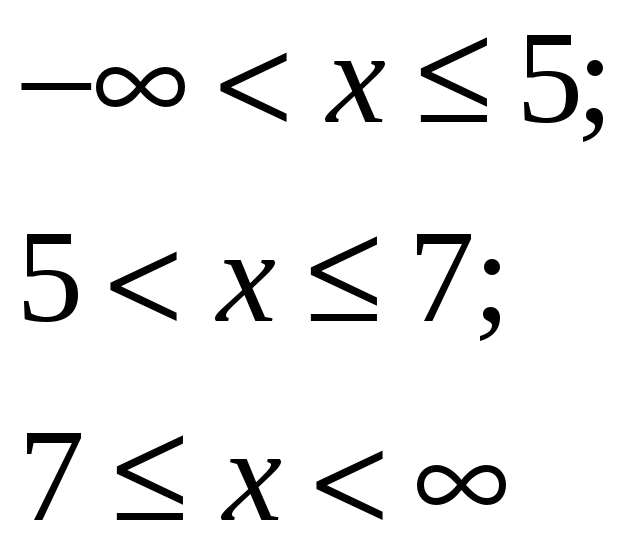
а)

б)

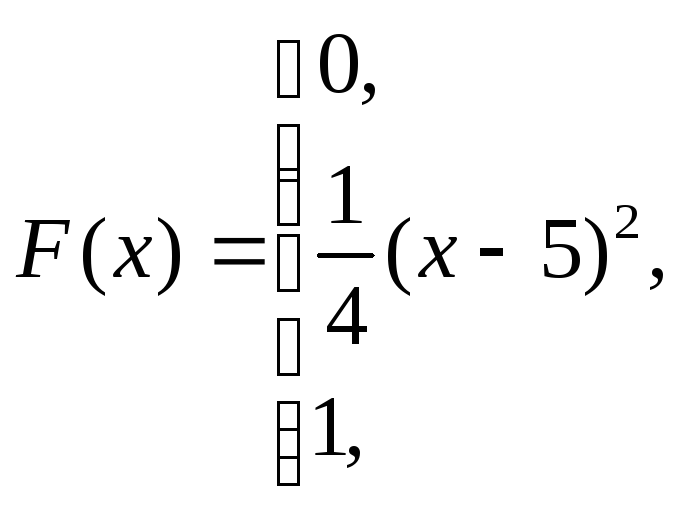
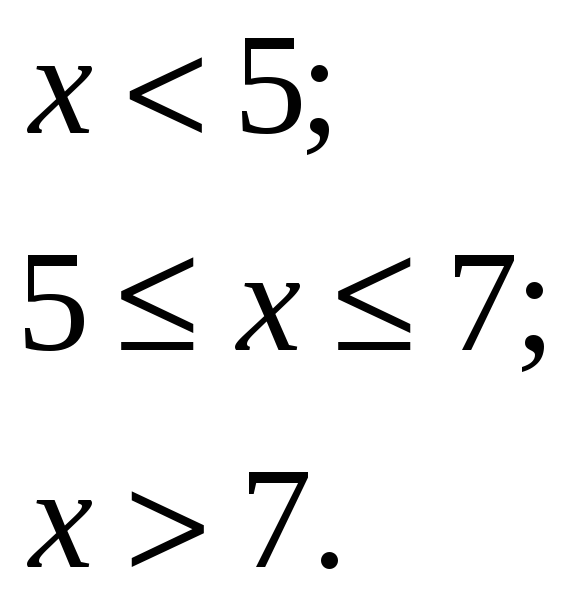
в)

г)

.

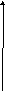
д) f(x) F(x)

1 1

0 1 2 3 4 5 6 7 x 0 1 2 3 4 5 6 7 x

Задача 8. Случайная величина имеет биномиальное распределение. Найти вероятность , если математическое ожидание =3, а дисперсия .

Решение:

В задаче надо найти. Для биномиального распределения M(X) и дисперсию D(X) находим по формулам:.

M(X) = np; D(x)=npq=np(1– p).

Тогда np =3. Отсюда

,

.

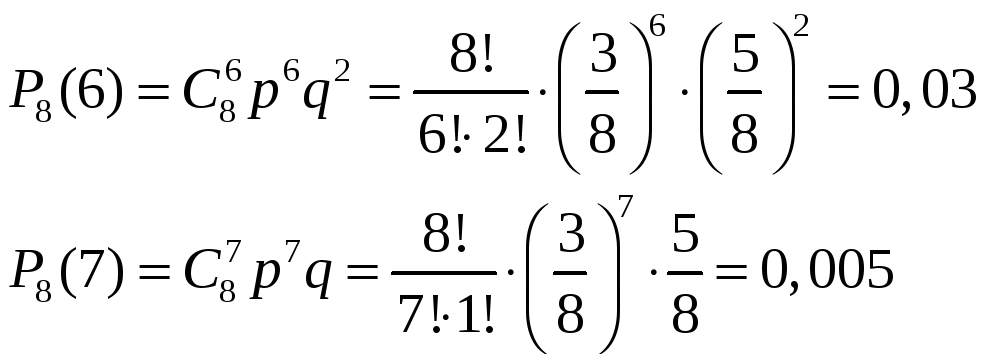
Ответ: Р(Х)=0,137

Задача 9. Случайные величины имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности , если у этих случайных величин математические ожидания и средние квадратические отклонения равны m.

Решение:

а) равномерное распределение:

.

Отсюда находим: .

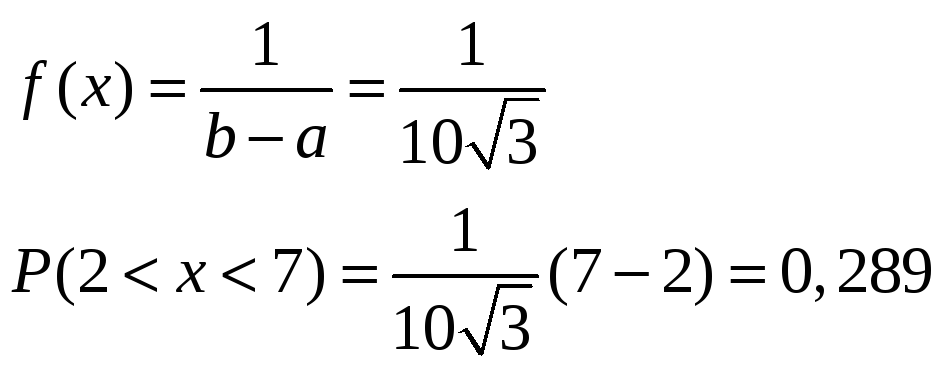
б) показательное распределение:

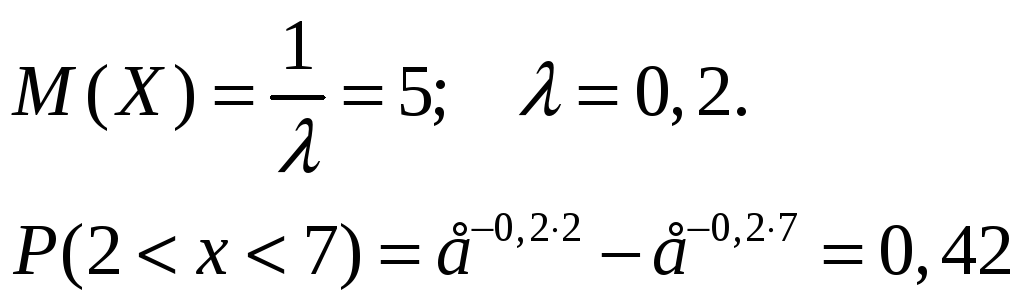
в) нормальное распределение:

а=5 ; б=5

Ответ: а)0,289; б)0,424 в)0,381

Задача 10. Выборка Х объемом измерений задана таблицей:

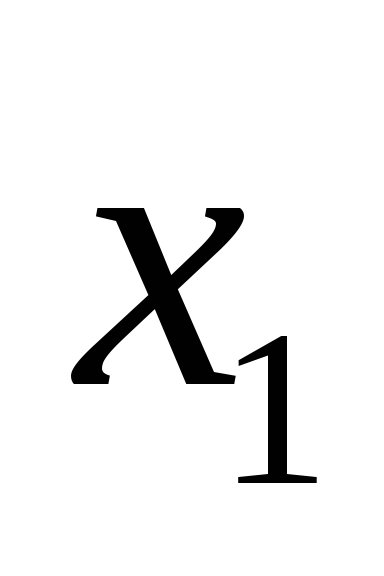
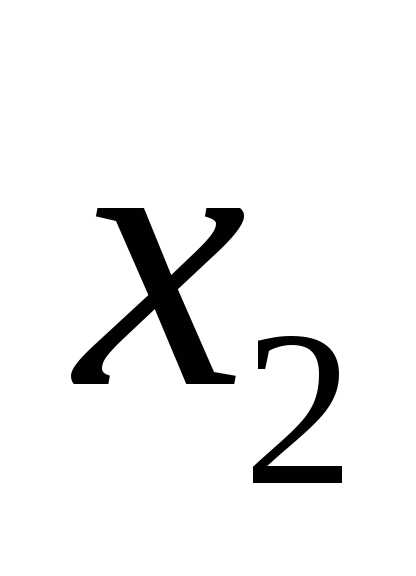
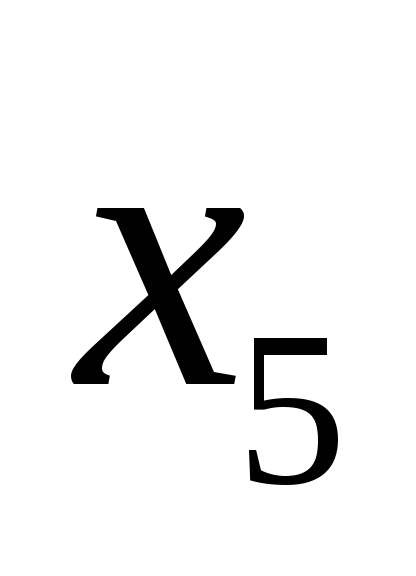
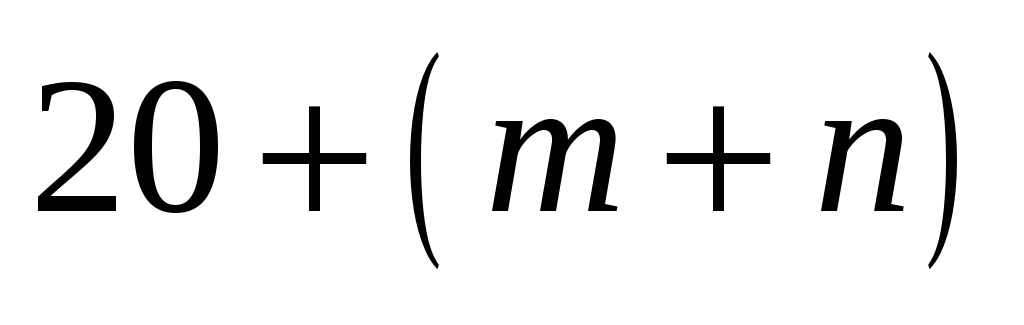
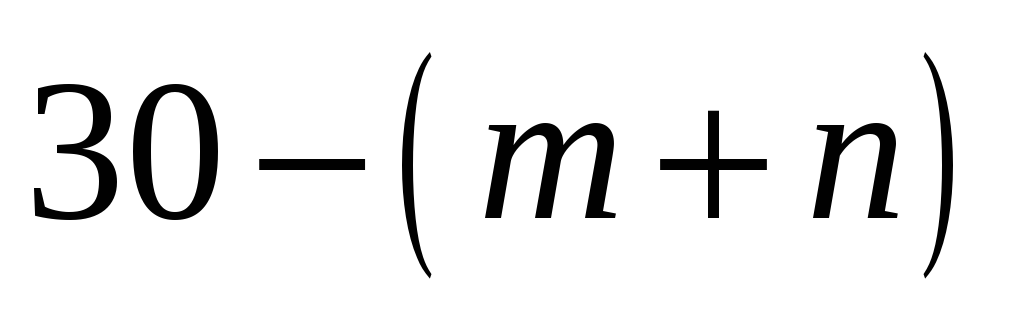
	5	13			19	10	3

результаты измерений;

частоты, с которыми встречаются значения .

а) Построить полигон относительных частот ;

б) вычислить среднее выборочное , выборочную дисперсию и среднее квадратическое отклонение ;

в) по критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости .

Решение:

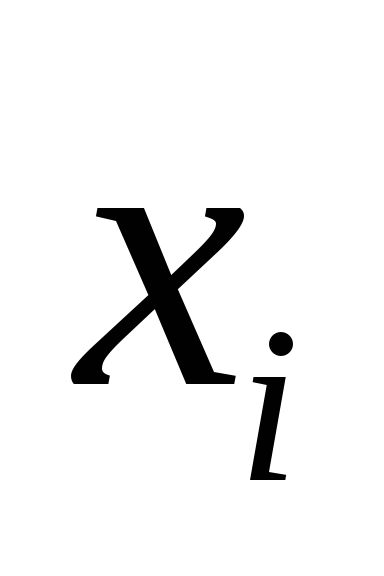
	1	1,6	2,2	2,8	3,4	4	4,6
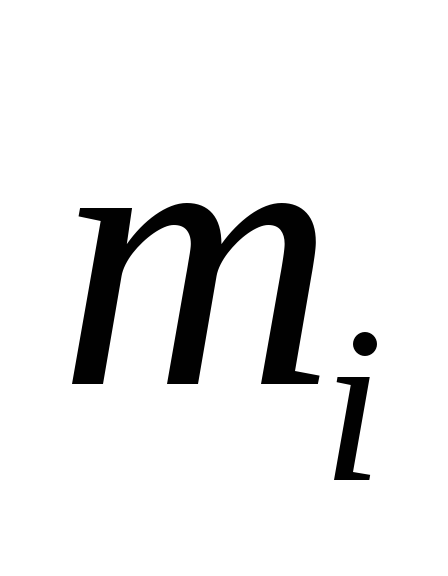
	5	13	27	23	19	10	3

а) Полигон относительных частот

0,3

0,2

0,1

0 1 2 3 4 5

б)

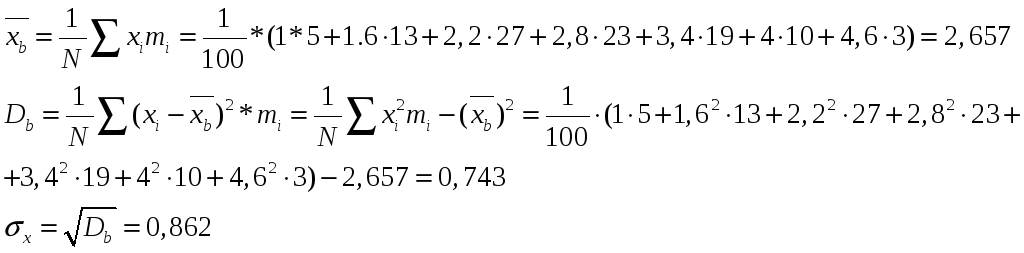
в) Найдем теоретические частоты

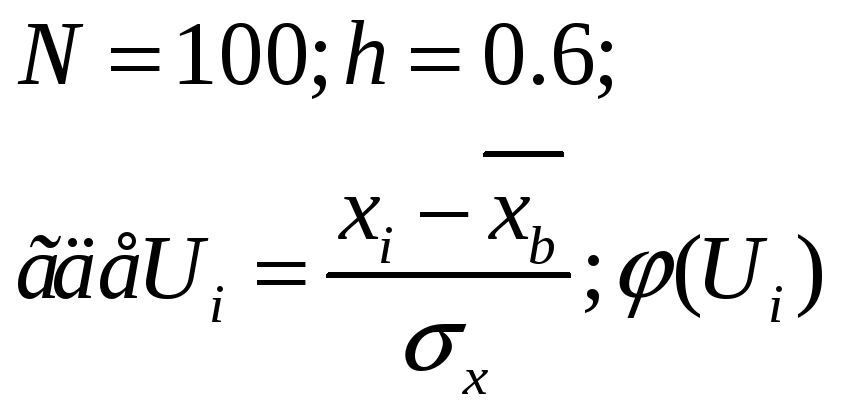-по таблицам

	1	1,6	2,2	2,8	3,4	4	4,6
	5	13	27	23	19	10	3
	-1,92	-1,23	-0,53	0,166	0,862	1,56	2,25
	0,0632	0,1872	0,3467	0,3932	0,2756	0,1182	0,0317
	4,397	12,99	24,05	27,28	19,12	8,20	2,20

Объединим малочисленные частоты:10+3=13; 8,20+2,20=10,4.Найдем наблюдаемое значение критерия Пирсона:

По таблице критических точек распределения при уровне значимости и числу степеней свободы к=6-3=3 находим .

Так как то можно принять гипотенузу о нормальном распределении генеральной совокупности.

6