Физика / ЛЕКЦИИ_1-ый_семестр / 1_МЕХАНИКА / II-Динамика / ЛК_№4-Классическая_динамика

5

Тема 2. Динамика материальной точки.

Лекция №4.

1. Силы гравитации.

2. Упругие силы.

3. Силы трения.

4. Динамика вращения материальной точки. Автомобиль на выпуклом мосту.

5. Примеры расчёта тяговых усилий при буксировке автомобиля.

Как показывает сравнение, гравитационные силы являются слабейшими из всех фундаментальных взаимодействий, однако они обладают свойствами аддитивности (суммируются!) и достигают значительных величин в космическом масштабе ( притяжение Луны, строение Солнечной системы и т.п.).

Величина гравитационной силы притяжения двух точечных масс m₁ и m₂ определена Ньютоном и известна как закон всемирного тяготения:

, ( 1 )

где расстояние между массами, а G = 6,67 10 ^-11 Н· м²/кг² - гравитационная

постоянная.

Чтобы подчеркнуть, что сила – это вектор, закон записывают несколько иначе, рассматривая силу, действующую на m₂ со стороны m₁:

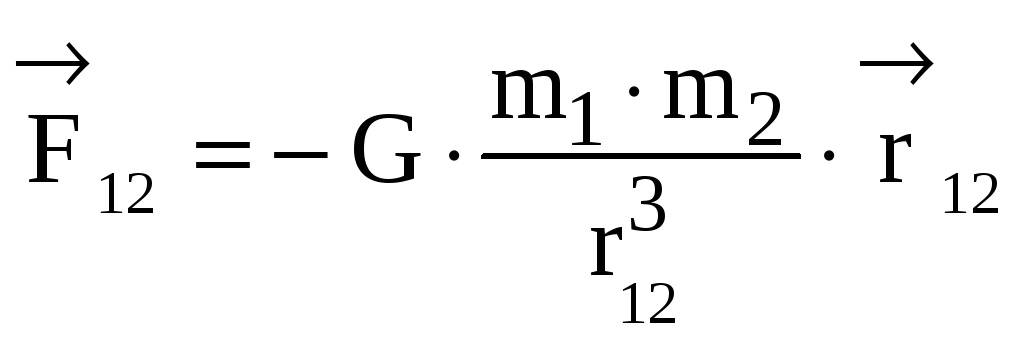, ( 2 )

Из формулы (2) видно направление силы (она направлена вдоль прямой, соединяющей взаимодействующие массы). Модуль силы притяжения P тела с массой m к Земле , которую называют силой тяжести можно записать так:

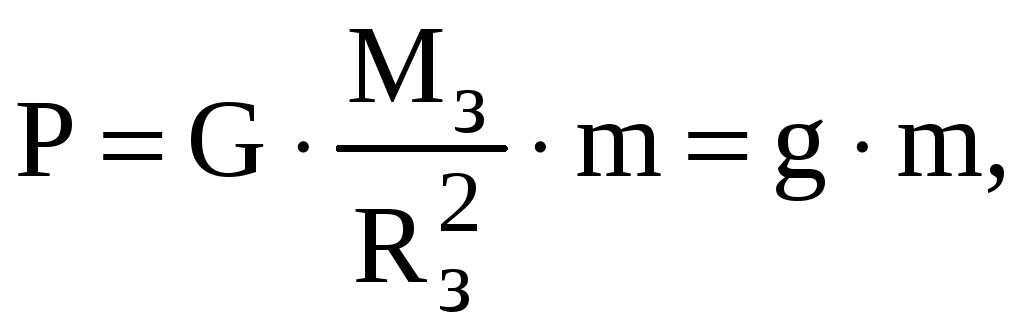( 3 )

где величина 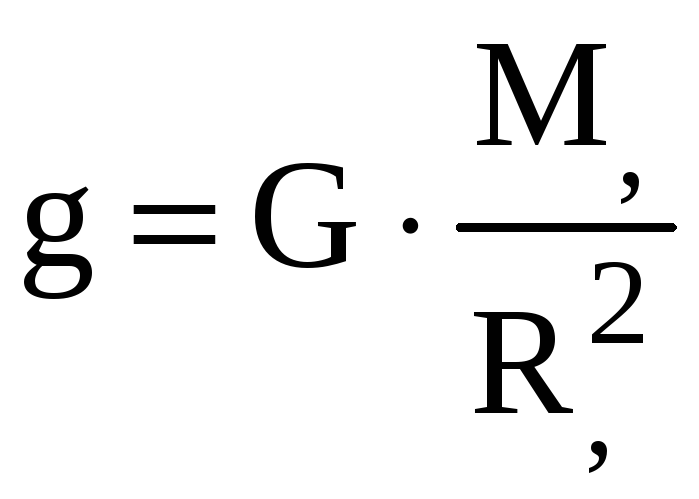- ускорение свободного падения, М_З- масса Земли,

а R_З – радиус Земли.

Из выражения для ускорения свободного падения g видно, что оно не зависит от массы выбранного тела и поэтому одинаково для всех тел в определенной точке земной поверхности.

Важно подчеркнуть различие двух понятий – силы тяжести и веса тела. Первая сила существует всегда, когда есть притягивающая масса М_З, тогда как вторая, представляющая меру воздействия тела на подставку или нить подвеса, вообще говоря может изменяться.

Для пояснения сказанного полезно рассмотреть показания весов, на которых стоит гиря (рисунок ниже!).

В неподвижном состоянии на гирю действует две силы - сила тяжести Р и сила реакции опоры ( весов ) N, причем Р - N = 0.

Если весы движутся вниз с ускорением а, то уравнение второго закона Ньютона, записанное в неподвижной системе координат, имеет вид:

ma = P - N , (4 )

Откуда

N = P - ma = mg - ma = m( g - a ). ( 5 )

По третьему закону Ньютона сила реакции опоры N равна и противоположно направлена по отношению к силе давления гири на весы , т.е. весу гири ( N = ).

Поэтому вес гири будет равен: = m (g - a). ( 6 )

Очевидно, при а = g = 0, т.е. все свободно падающие тела ничего не весят.

2. Упругие силы.

Кроме гравитационных сил в механике рассматриваются упругие силы (иначе, силы упругости!) и силы трения.

Силы упругости обусловлены деформациями. Деформации связаны с изменением взаимного расположения молекул, образующих рассматриваемое тело, причем силы возникают лишь тогда, когда деформации носят упругий характер.

В этом случае справедлив закон Гука так, что

, ( 1 )

где обозначает величину упругой деформации, очевидно, что при

растяжении тела, при сжатии,

- коэффициент пропорциональности, зависящий от свойств деформируемого

тела и вида деформации.

Вычислим работу, совершаемую против упругой силы, при деформации на величину одномерного стержня, показанного на рисунке .

По определению .

Эта работа идет на изменение взаимного расположения отдельных частей тела, т. е. на изменение его потенциальной энергии.

Следовательно, зависимость потенциальной энергии стержня от величины его деформации имеет вид:

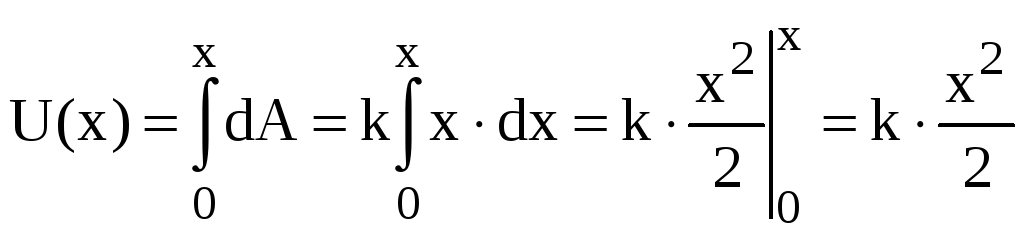, (2).

3. Силы трения.

Наиболее общим примером проявления упругих сил служат силы сжатия-растяжения пружин.

Рассмотрение сил трения можно ограничить двумя примерами: силами сухого и силами вязкого трения.

а) Сила сухого трения:

F_тр = –  ·N, ( 2 )

где  - коэффициент трения, характеризующий свойства взаимодействующих

поверхностей, а N - так называемая сила нормального давления.

В отличие от сил вязкого трения эта сила не зависит от скорости движения тела.

б) Сила вязкого трения (ранее встречалась в задаче о демпфирующем устройстве – амортизаторе колебаний колеса автомобиля!), напротив, зависит от величины скорости, причем степень зависимости меняется по мере возрастания скорости.

Для сравнительно небольших скоростей она может быть представлена в таком виде:

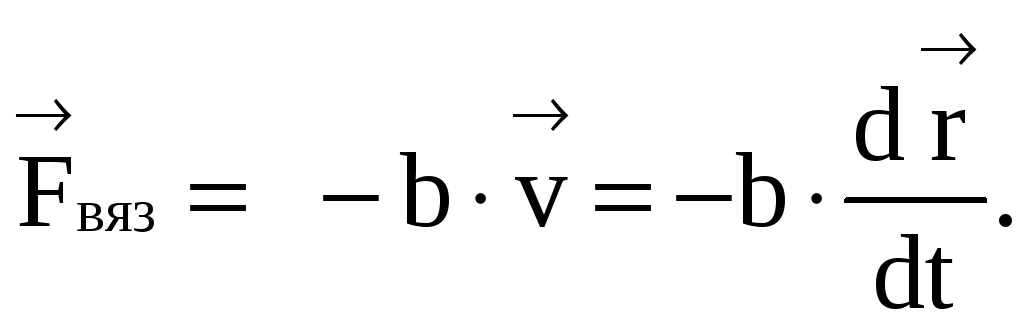( 3 )

Величина коэффициента b зависит как от свойств самого тела, которое движется в вязкой среде, так и от свойств среды.

Практически важное значение имеет сила трения покоя, возникающая между соприкасающимися телами. Максимальную величину этой силы обычно оценивают по формуле для силы трения скольжения.

3. Динамика вращения материальной точки. Автомобиль на выпуклом мосту.

Здесь присутствуют некоторые интересные особенности.

Если выбирать обычную неподвижную систему координат, то при вращении направления скоростей и ускорения точки будут ежесекундно изменяться относительно координатных осей, что не совсем удобно. Поэтому оперируют с так называемой следящей системой координат, т.е. с такой системой, начало которой неподвижно и совпадает в выбранный момент времени с движущейся материальной точкой, а направления ее осей совпадает с направлением скорости тела в этот момент времени и с направлением радиуса вращения, проведенного в точку, где расположено тело в этот же момент времени.

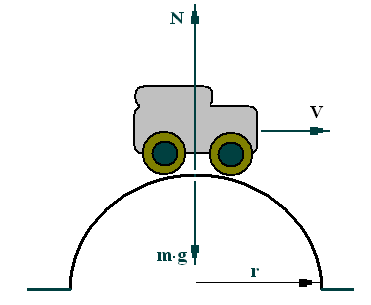
Важно отметить, что выбранная таким образом система отсчета является неподвижной относительно инерциальной системы отсчета (например, Земли), и в ней справедливы законы Ньютона.

Рассмотрим в качестве примера движение автомашины по выпуклому мосту, радиус которого равен r. Направим одну из осей следящей системы координат к центру моста, а другую – вдоль направления скорости v.

Уравнение движения в этом случае имеет вид ( в проекции на вертикальную ось):

ma_ц = mg - N, ( 1 )

где а_ц – центростремительное ускорение,

N – сила реакции моста, mg - сила тяжести.

Решая это уравнение относительно N, получаем, что

N = mg - ma_ц = m(g -). ( 2 )

Откуда следует, что при = g сила реакции моста будет равна 0.

Но это означает, что автомашина в этот момент времени не оказывает никакого давления на мост, т.е. она находится в состоянии невесомости.

4. Примеры расчёта тяговых усилий при буксировке автомобиля.

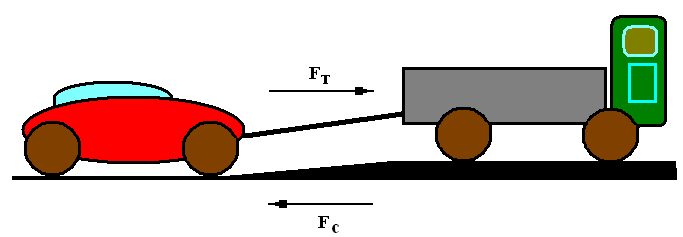
Пример №1.

Автомобильный тягач буксирует автомобиль с заблокированными колёсами. Вес буксируемого автомобиля тонн. Тягач развивает достаточно большое тяговое усилие. Определить величину силы, начиная с которой буксируемый автомобиль придёт в движение, если коэффициент сухого трения между колёсами автомобиля и поверхностью дорожного покрытия составляет ~ .

Решение.

Буксируемый автомобиль представляется механической системой, на которую действует сила тяги – и сила сопротивления – .

Последняя представляет собой силу сухого трения – где коэффициент сухого трения (по условию – ), нормальная сила давления автомобиля на поверхность дороги (может быть принята равной весу автомобиля, то есть, кг по условию).

С помощью второго закона Ньютона составляем уравнение движения буксируемого автомобиля:

.

Очевидно, движение должно иметь место при . Как видно из уравнения движения, это возможно, когда его правая часть больше нуля, то есть, . С учётом чисел в условии получаем, что буксируемый автомобиль начнёт движение, когда сила тяги кг!

Задание. Перейти к единицам системы СИ!

Пример № 2.

В условиях предыдущего примера считать, что тяговый трос выполнен из витой сталистой проволоки и может рассматриваться как упругая пружина с коэффициентом упругости – кг/м. Определить величину удлинения троса в момент начала движения буксируемого автомобиля.

Решение.

Сила упругости пружины – удлинение прижины [м].

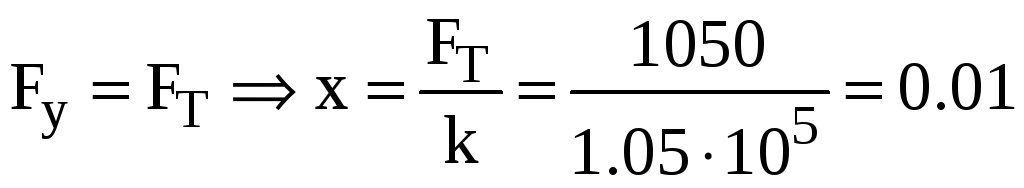Очевидно, что в момент начала движения трос должен испытывать действие силы кг, то есть, м.

Задание. Перерейти к единицам системы СИ!