
- •Практичне заняття № 2 Тема:Лінійні оператори в векторних просторах
- •1. Лінійні оператори і матриці лінійних операторів
- •3. Детермінант мтариці.
- •4. Характеристичний та мінімальний многочлени матриці
- •5. Мінімальний многочлен вектора відносно матриці
- •6. Власний, інваріантний та циклічний підпростори лінійного оператора
- •Зміст практичного заняття
Практичне заняття № 2 Тема:Лінійні оператори в векторних просторах
Мета заняття: Засвоїти поняття лінійного оператора в векторному просторі над полем, методи виконання дій з лінійними операторами і їх матрицями, побудови характеристичного та мінімального многочленів матриці, мінімального многочлена вектора відносно матриці, інваріантного та циклічного підпросторів лінійного оператора.
Короткі теоретичні відомості
1. Лінійні оператори і матриці лінійних операторів
Нехай
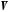 – векторний простір над полем
– векторний простір над полем
Означення.
Лінійним
оператором
 у
векторному просторі
у
векторному просторі
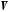 називається
відображення
називається
відображення
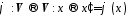 таке, що виконані наступні умови (умови
лінійності):
таке, що виконані наступні умови (умови
лінійності):
1)
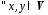
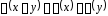 ;
;
2)


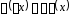 .
.
Найпростіші властивості лінійного оператора:
1) Образом
нуль-вектора є нуль-вектор:
 .
.
2) Образом
вектора, протилежного довільному вектору
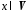 є вектор, протилежний образу вектора
є вектор, протилежний образу вектора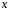 :
: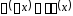
3) Образом
лінійної комбінації довільних векторів
 простору
простору є лінійна комбінація (з тими ж коефіцієнтами)
образів цих векторів:
є лінійна комбінація (з тими ж коефіцієнтами)
образів цих векторів:
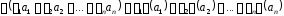
Теорема.
Нехай
 – лінійний оператор у векторному
просторі
– лінійний оператор у векторному
просторі ,
,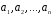 – базис в
– базис в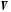 .
Тоді лінійний оператор
.
Тоді лінійний оператор однозначно визначається заданням
образів
однозначно визначається заданням
образів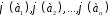 векторів базису
векторів базису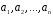 .
.
Нехай
у векторному просторі
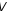 заданий деякий базис
заданий деякий базис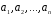 .
.
Означення.
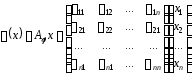
Матрицею
лінійного оператора
 в базисі
в базисі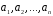 називається матриця
називається матриця
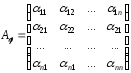 ,
,
елементами
якої є коефіцієнти в розкладі образів
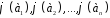 векторів
векторів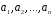 за базисом
за базисом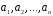 ,
тобто
,
тобто
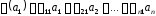 ;
;
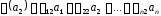 ;
;
………………………………………..
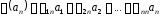 .
.
З
означення випливає, що стовпцями матриці
 є координатні рядки векторів
є координатні рядки векторів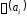 ,
, ,
в базисі
,
в базисі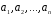 .
.
У
координатному вигляді дія лінійного
оператора
 на
вектор
на
вектор
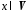 зводиться до множення матриці лінійного
оператора
зводиться до множення матриці лінійного
оператора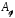 на координатний стовпчик вектора
на координатний стовпчик вектора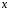 :
:
 .
.
Ясно,
що матриця оператора
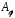 залежить від вибору базису простору
залежить від вибору базису простору .
.
2. Дії з лінійними операторами зводяться до відповідних дій з матрицями лінійних операторів.
3. Детермінант мтариці.
Означення.
Оберненим
оператором
до лінійного оператора
 називається лінійний оператор
називається лінійний оператор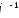 такий, що
такий, що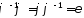 .
.
Матриця
оператора
 ,
який має обернений, є квадратною
невиродженою матрицею. Добуток квадратної
матриці порядку
,
який має обернений, є квадратною
невиродженою матрицею. Добуток квадратної
матриці порядку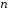 на матрицю-стовпець можна розглядати
як операцію над вектором. Ця операція
є лінійним перетворенням
на матрицю-стовпець можна розглядати
як операцію над вектором. Ця операція
є лінійним перетворенням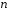 -вимірного
векторного простору. Квадратна матриця
називається оборотною, якщо згадане
лінійне перетворення є взаємно
однозначним.
-вимірного
векторного простору. Квадратна матриця
називається оборотною, якщо згадане
лінійне перетворення є взаємно
однозначним.
Загальний
критерій оборотності матриці формулюється
за допомогою поняття визначника
(детермінанта). Детермінант матриці
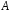 над полем
над полем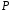 є елементом поля
є елементом поля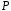 .
Він є функцією всіх елементів матриці
і позначається через
.
Він є функцією всіх елементів матриці
і позначається через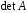 або
або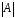 .
.
Теорема
(критерій оборотності матриці). Матриця
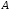 оборотна тоді і тільки тоді, коли
оборотна тоді і тільки тоді, коли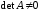 .
.
Щоб
визначити поняття детермінанту матриці
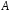 порядку
порядку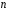 ,
введемо наступні поняття.
,
введемо наступні поняття.
Нехай
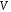 – скінченна множина з
– скінченна множина з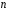 елементів.
елементів.
Підстановкою
порядку
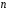 на множині з
на множині з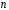 елементів називається взаємно однозначне
відображення множини
елементів називається взаємно однозначне
відображення множини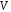 на себе.
на себе.
Підстановку
можна представити у вигляді дворядного
запису:
 .
.
Очевидно,
обернене перетворення має вигляд
 .
.
Підстановки
утворюють групу відносно операції
композиції, яка позначається
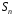 Порядок групи підстановок
Порядок групи підстановок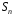 дорівнює
дорівнює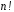 .
.
Підстановку
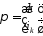 можна задати (представити) як матрицю.Існує
ізоморфне відображення
можна задати (представити) як матрицю.Існує
ізоморфне відображення
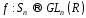 .Матриця
вигляду
.Матриця
вигляду
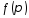 ,
,
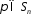 ,
називається матрицею підстановки, або
підстановочною матрицею.
,
називається матрицею підстановки, або
підстановочною матрицею.
В
підстановочній матриці
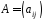 порядку
порядку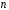 елементи з індексами
елементи з індексами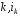 дорівнюють одиниці, а інші елементи
дорівнюють нулю.
дорівнюють одиниці, а інші елементи
дорівнюють нулю.
Кожну
підстановку
 можна представити у вигляді добутку
можна представити у вигляді добутку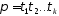 деяких спеціальних підстановок, як
називаються циклами, причому цикли
деяких спеціальних підстановок, як
називаються циклами, причому цикли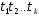 попарно незалежні. Останнє означає, що
підстановки
попарно незалежні. Останнє означає, що
підстановки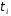 і
і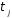 ,
при
,
при ,
діють на підмножинах підстановки, що
не перерізаються, якщо не брати до уваги
елементи, що залишаються нерухомими.
,
діють на підмножинах підстановки, що
не перерізаються, якщо не брати до уваги
елементи, що залишаються нерухомими.
Нехай
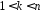 и
и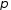 – підстановка степеня
– підстановка степеня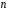 ,
причому
,
причому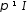 .
.
Означення.
Підстановка
 називається
називається -членнимциклом,
якщо вона не переміщає
-членнимциклом,
якщо вона не переміщає
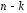 елементів, а її дію на ті елементи, що
залишилися,
елементів, а її дію на ті елементи, що
залишилися,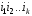 можна представити у вигляді циклічної
діаграми переходів:
можна представити у вигляді циклічної
діаграми переходів:
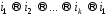 .
У цій діаграмі допускається лише один
перехід від елементу з більшим індексом
до елементу з меншим індексом, а саме:
.
У цій діаграмі допускається лише один
перехід від елементу з більшим індексом
до елементу з меншим індексом, а саме: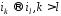 .
.
Означення.
Цикловою
структурою
підстановки
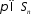 називається запис виду
називається запис виду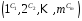 ,
який означає, що
,
який означає, що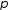 розкладається в добуток
розкладається в добуток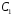 циклів довжини 1,
циклів довжини 1,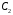 циклів довжини 2, і так далі,
циклів довжини 2, і так далі,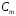 циклів довжини
циклів довжини .
.
Найбільш простим циклом, очевидно, є підстановка, яка переставляє місцями лише два елементи.
Означення. Цикл довжини 2 називається транспозицією.
Транспозиції не обов'язково є незалежними циклами.
Нехай
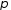 – підстановка з
– підстановка з
 ,
,
 – будь-який її розклад в добуток
транспозицій. Тоді число
– будь-який її розклад в добуток
транспозицій. Тоді число
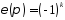 ,
яке називається знаком (або сигнатурою,
або парністю
,
яке називається знаком (або сигнатурою,
або парністю
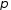 )
повністю визначається підстановкою
)
повністю визначається підстановкою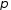 і не залежить від способу розкладу
і не залежить від способу розкладу в добуток транспозицій.
в добуток транспозицій.
Означення.
Визначником
матриці
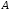 порядку
порядку над полем
над полем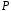 називається знакозмінна сума всіх
членів визначника, що відповідають
підстановкам групи
називається знакозмінна сума всіх
членів визначника, що відповідають
підстановкам групи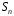 :
: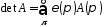 .
.
В
розгорнутому вигляді формула для
обчислення визначника матриці
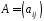 має вигляд:
має вигляд:
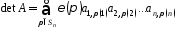 .
.
Ця формула називається формулою повного розгортання визначника.
У деяких
криптографічних застосуваннях виникає
задача
Лагранжа,
яка полягає в знаходженні всіх розв’язків
рівняння
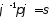 при заданих
при заданих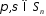 ,
тобто в знаходженні всіх спряжених
підстановок. Розв’язки рівняння
,
тобто в знаходженні всіх спряжених
підстановок. Розв’язки рівняння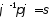 можна отримати за допомогою «оператора
Лагранжа»
можна отримати за допомогою «оператора
Лагранжа»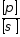 .
.
Нехай
 ,
Розглянемо множину
,
Розглянемо множину всіх різних перестановок циклів, що
входять до циклічного запису підстановки
(включаючи цикли довжини 1). Маємо
всіх різних перестановок циклів, що
входять до циклічного запису підстановки
(включаючи цикли довжини 1). Маємо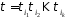 .
Виписування окремого циклу можна
здійснювати з довільного елемента
циклу, тобто з довільним циклічним
зсувом вліво, наприклад,
.
Виписування окремого циклу можна
здійснювати з довільного елемента
циклу, тобто з довільним циклічним
зсувом вліво, наприклад, .
.
Нехай
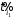 – довільний циклічний зсув
– довільний циклічний зсув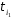 вліво. Тоді можна записати
вліво. Тоді можна записати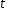 ще у більшій кількості варіантів. Множину
цих варіантів запису
ще у більшій кількості варіантів. Множину
цих варіантів запису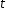 у виді
у виді позначимо через
позначимо через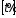 .
.
Оператор
Лагранжа
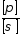 задає множину розв’язків
задає множину розв’язків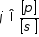 рівняння
рівняння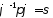 ,
що будуються наступним чином:
,
що будуються наступним чином:
1)
виписуємо одну довільну перестановку
циклів
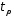 з множини
з множини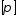 ,
під нею почергово записуємо перестановки
циклів
,
під нею почергово записуємо перестановки
циклів з
з ,
але такі, щоб над відповідним циклом
довжини
,
але такі, щоб над відповідним циклом
довжини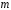 з циклічного запису підстановки
з циклічного запису підстановки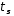 був розташований цикл з циклічного
запису підстановки
був розташований цикл з циклічного
запису підстановки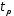 тієї ж довжини
тієї ж довжини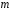 ;
;
2) будуємо чергову підстановку, забираючи дужки з запису циклів.
