Матан

Приклад Задані дві множини цілих чисел: 1 1;2;3;4 та 2 8;9;10 з кожної множини беруть по одному числу. Побудувати простір елементарних подій експерименту і такі випадкові події: 1) А – сума пари чисел кратна; 2) В – сума пари чисел кратна 5. Знайти P(A); P (B); P( A B ); P( A B ); P ( A / B )

Рішення Запишемо простір елементарних подій експерименту, оскілки перша

множина містить 4 елементи, а друга – 3 вочевидь можливих подій буде

4х3=12:

1)	1;8 ; 2)	1;9 3)	1;10 ; 4) 2;8 ; 5)	2;9 6)	2;10
7)	3;8 ; 8)	3;9 9)	3;10 ; 10) 4;8 ;	11) 4;9	12) 4;10

Подія А складається з таких елементарних подій:

А= 1,9 ; 2,8 ; 2,10 ; 3,9 ; 4,8 ; 4;10 . Цих подій – 6. Отже, ймовірність події

А: P ( A) 6 1 . 12 2

Подія В складається з таких елементарних подій:

В= 1,9 ; 2,8 . Цих подій – 2. Отже, ймовірність події В:

A B A 1,9 ; 2,8 ; 2,10 ; 3,9 ; 4,8 ; 4;10 , отже P ( A B )

A B B 1,9 ; 2,8 , отже P A B P ( B )		2						1
		12			6
A / B 2,10 ; 3,9 ; 4,8 ; 4;10 , отже P ( A / B )		4					1

12 3

P ( B ) 2 1 . 12 6

6 1

12 2

Приклад Яка ймовірність того, що навмання кинута в круг точка потрапить в 4-х кутник вписаний в цей круг.

Рішення Оскільки в коло можна вписати безліч чотирикутників, будемо вважати,

що даний чотирикутник правильний, тобто квадрат. Зобразимо дану ситуацію геометрично:

R

	Позначимо радіус круга як	R ,		тоді площа круга дорівнює: S кр R 2 ,
	площа квадрата дорівнює: S кв	(		2			R ) 2 2 R 2 . Імовірність попадання в
				2

квадрат дорівнює відношенню площ:

P Pкв 2

Pкр

Приклад Студент отримав стовпчики із 15 дат та 15 подій. Йому потрібно вказати дату кожної події, при чому він може використати кожну дату тільки один раз. Студент знає дати для 4-х подій, а для решти він це робить випадковим методом. Знайти імовірність того, що він правильно датує кожну подію.

Рішення Нехай студент відібрав дати для тих подій, які він знає. В нього

залишилося ще 11 дат і 11 подій, для яких він робить вибір випадково. Тоді ймовірність події А – студент датував правильно кожну подію є добуток ймовірностей подій правильного датування кожної події:

P ( A)	1		1	...	1			1	2,5 10 8
11		10		1			11!

Приклад В групі 6 студентів. Яка ймовірність того, що дні народження студентів не збігаються.

Рішення В році 365 днів, а отже для групи з 6 осіб ймовірність того, що дні

народження не збігаються можна записати у вигляді формули:

		1				2				3				4				5			365 !
P (6 ) 1 1				1				1				1				1							0,96
																					365 6 365
		365				365				365				365				365				6 !

Приклад В урні містяться 4 червоні, 5 білих та 4 зелених кульок. Навмання із урни беруть три кульки, яка ймовірність того, що вони виявляться різного кольору.

Рішення

Всього кульок 4+5+4=13.

Ймовірність події А – всі кульки різного кольору складається з суми ймовірностей наступних подій:

А1 – першою витягли червону кульку, другою білу, третьою – зелену А2 – першою витягли червону кульку, другою зелену, третьою – білу А3 – першою витягли білу кульку, другою червону, третьою – зелену А4 – першою витягли білу кульку, другою зелену, третьою – червону А5 – першою витягли зелену кульку, другою білу, третьою – червону А6 – першою витягли зелену кульку, другою червону, третьою – білу. Знайдемо ймовірності даних подій:

P ( A )		4			5					4
1	13		12					11
P ( A3 )		5				4					4
	13
			12					11
P ( A5 )		4					5					4
	13
			12					11

;

;

;

P ( A2	)		4						4						5
		13
								12						11
P ( A4	)				4						4						5
		13						12						11
P ( A6	)			4						4						5
		13						12						11

6

P ( A ) Ai 6 0,0466 0,28

i 1

Приклад Студент знає 45 з 60 питань програми. Кожен екзаменаційний білет складається з трьох питань. Знайти ймовірність того, що студент знає:

1)три питання свого екзаменаційного білету.

2)два питання свого екзаменаційного білету;

3)одне питання свого екзаменаційного білету.

Рішення Ймовірність події А- студент знає три питання екзаменаційного білету

складається з добутку ймовірностей таких подій: А1 – студент знає відповідь на перше питання; А2 – студент знає відповідь на друге питання; А3 – студент знає відповідь на третє питання;

P ( A) 45 44 43 0,415 . 60 59 58

Ймовірність події В – студент знає два питання екзаменаційного білету складається з суми ймовірностей таких подій:

P ( B ) P ( A1 ) P ( A2 ) P ( A3 ) P ( A1 ) P ( A2 ) P ( A3 ) P ( A1 ) P ( A2 ) P ( A3 )

	45		44		15		45		15		44		15		45		44	0,434
60		59		58		60		59		58		60		59		58

Ймовірність події С – студент знає одне питання екзаменаційного білету складається з суми ймовірностей таких подій:

P (C ) P ( A1 ) P ( A2 ) P ( A3 ) P ( A1 ) P ( A2 ) P ( A3 ) P ( A1 ) P ( A2 ) P ( A3 )

	45		15		14		15		14		45		15		45		14	0,138
60		59		58		60		59		58		60		59		58

Приклад До складального цеху надходять деталі від трьох інших цехів. Від першого надходить 40% усіх деталей, від другого 32% і від третього решта. Перший цех допускає в середньому 0,04 браку, другий 0,1 і третій

0,05 браку.

1.Яка ймовірність того, що до складального цеху надійде стандартна

деталь.

2.До складального цеху надійшла стандартна деталь, яка ймовірність того, що вона з другого цеху.

Рішення Кількість деталей, що надійшли з третього цеху дорівнює: 100-40-

32=28%

Висунемо гіпотези:

Н1 – стандартна деталь надійшла з першого цеху: Р(Н1)=0,4; Н2 – стандартна деталь надійшла з другого цеху: Р(Н2)=0,32; Н3 – стандартна деталь надійшла з третього цеху: Р(Н3)=0,28;

Ймовірність того, що перший цех виготовить стандартну деталь дорівнює 1-0,04=0,96.

Ймовірність того, що другий цех виготовить стандартну деталь дорівнює 1-0,1=0,9.

Ймовірність того, що третій цех виготовить стандартну деталь дорівнює

1-0,04=0,95.

1)Подія А – д складального цеху надійшла стандартна деталь. За формулою повної ймовірності:

Р(А)=0,4∙0,96+0,32∙0,9+0,28∙0,95=0,938

2)Ймовірність події В - стандартна деталь з другого цеху визначається за формулою Байеса:

P ( H 2	/ A)		0,32 0,9			0	,288	0,3
		0,4 • 0,96	0,32 • 0,9	0,28 • 0,95			,938
					0

Приклад Імовірність появи події А в кожному випробуванні дорівнює 0,6. Знайти імовірність того, що при 100 випробуваннях подія А з’явиться:

1)70 разів;

2)від 40 до 50 разів;

3)не більше 60 разів.

Рішення 1) Скористаємося формулою Бернуллі:

де n=100; k=70; p=0,6; q=1-0,6=0,4

2) Використаємо інтегральну формулу Лапласа:

					k			2 np							k 1 np
P k k k Ф															Ф
n 1			2						npq								npq
np 100			0,6 60
	npq		100 0,6 0,4					24							4,9
Pn 40			k 50		50 60											40 60
					Ф										Ф						Ф(4) - Ф(2)	0,99 - 0,8227	0,1673
								4,9								4,9

3) Не більше 60 разів це від 0 до 60. Використаємо інтегральну теорему Лапласа:

	60		60			0 60
Pn 0	k 60 Ф				Ф			Ф(12)	0, 5
			4,9			4,9

Приклад. Імовірність того, що радіосигнал буде прийнятий при кожній з 6 передач, дорівнює 0,6.

1)Побудувати закон розподілу випадкової величини Х – кількості прийнятих радіосигналів.

2)Побудувати функцію розподілу ймовірностей і накреслити її графік.

3)Знайти математичне сподівання М(Х), дисперсію D(x), середньоквадратичне відхилення .

4)Знайти моду (Мо)

5)Знайти Р(1<X<3)

Рішення

У цьому прикладі x - дискретна випадкова величина, що приймає значення 0,1,2,3,4,5,6. Щоб побудувати ряд розподілу x , потрібно знайти ймовірності, з якими вона приймає ці значення. У цьому випадку є послідовність випробувань за схемою Бернуллі, тому що випробування незалежні, і ймовірність успіху р =0,6 однакова у всіх випробуваннях. Тоді по формулі Бернуллі при n=6, p=0,6, q=1- p=0,4:

P ( x	0 ) C 60	0,6 0	0,4 6	0,004096
P ( x	1) C 61	0,6 1 0,4 5		0,036864
P ( x	2 ) C 62	0,6 2	0,4 4	0,13824
P ( x	3) C 63	0,6 3	0,4 3	0,27648
P ( x	4 ) C 64	0,6 4	0,4 2	0,31104
P ( x	5) C 65	0,6 5	0,4 1	0,186624
P ( x	6 ) C 66	0,6 6	0,4 0	0,046656

Побудуємо ряд розподілу:

Значен	0	1	2	3	4	5	6	Сумма
ия х
Р	0,004096	0,036864	0,13824	0,27648	0,31104	0,186624	0,046656	1
x 1 p i	0	0,036864	0,27648	0,82944	1,24416	0,93312	0,279936	3,6
x 2 i p i	0	0,036864	0,55296	2,48832	4,97664	4,6656	1,679616	14,;4

2) Запишемо аналітичний вираз функції розподілу:

0, если х 0

		0,004694,	если	0 х 1
	0,04096,		если 1 х 2
		0,1792,	если 2 х 3
F ( x )		0,45568 ,	если	3 х 4
		0,76672,	если	4 х 5
	0,953344,		если	5 х 6
		1, если 6		х

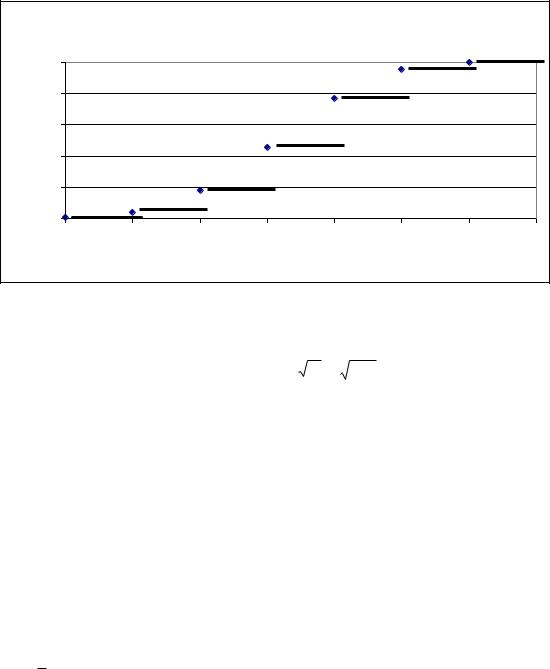
					Закон розподілу
			1
		0,8
	)	0,6
	Р(Х	0,4
		0,2
			0
			0	1	2	3	4	5	6	7
							Х
						6
3)	Математичне сподівання M ( X ) x i p i 3,6
						i 1
Дисперсія: D ( X ) M ( X 2 ) M 2 ( X ) 14 ,4 12 ,96								1,44 .
Середньоквадратичне відхилення							D	1,44 1,2 .
4)	Мода дискретної випадкової величини це її значення, що має
найбільшу ймовірність:
Mo 4 .
5)	P (1 x 3) P (2) 0,13824
Приклад.				Випадкова	величина	Х	задана	функцією	розподілу	F ( x ) .
Знайти:
1)	диференціальну функцію f ( x ) щільність розподілу,
2) математичне сподівання M ( x ), дисперсію D ( x ) , середньоквадратичне
відхилення .
3)	моду Mo та медіану Me ;
4)		1	X
	P			2
	2
Побудувати графіки функції та щільність розподілу.

0, при х 0

			2
F ( x )		х			, при 0	х	10
		100
				1, при х 10

Рішення 1) Щільність розподілу знайдемо як похідну функції розподілу:

0, при х 0

	f ( x )	F / ( x )		х	, при 0	х	10
				50
					0, при х 10

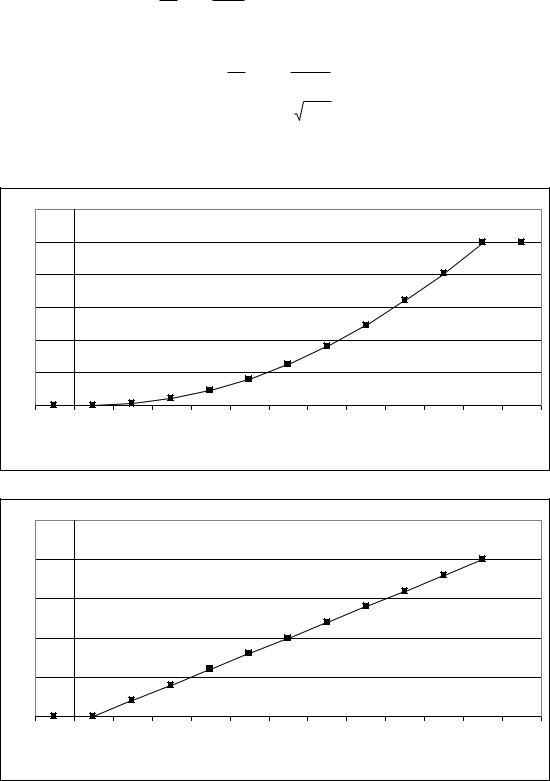
2) математичне сподівання:
			10	x 2	dx	1000			6,67
M ( X ) x f ( x )dx				50		150
			0
Дисперсію знайдемо за формулою:
						10	x	3	dx 10000
D ( X ) x 2		f ( x )dx M 2			( X )							50 44 ,44		5,56
						0	50				200
середньоквадратичне відхилення											5,56	2,26 .
3) Графіки функцій
	1,2
	1
	0,8
F(X)	0,6
	0,4
	0,2
	0
	-1	0	1	2	3				4	5	6	7	8	9	10	11
										Х
	0,25
	0,2
f(X)	0,15
	0,1
	0,05
	0
	-1	0	1	2	3				4	5	6	7	8	9	10
										Х
З графіка видно, що найбільше значення ймовірності досягається при
X 10 , отже модою є Mo ( X ) 10 .
Медіану знайдемо з виразу:

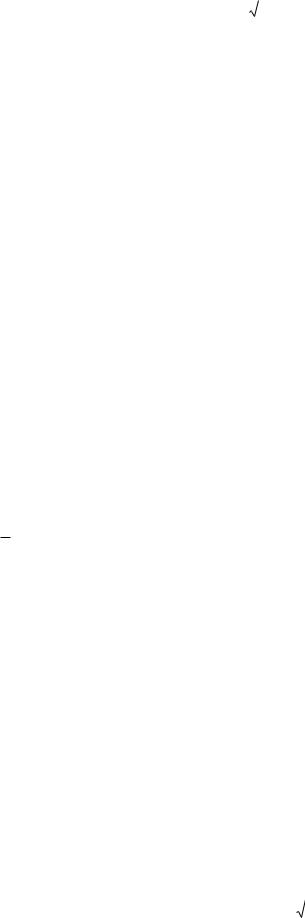
	1	b					x	2			b			b	2		1
			f ( x )dx															b 2			50 7,07
2						100					0		100				2
		0
4)				1
			P		X				2					F (2) F (0,5)						0,04 0,025			0,0375
			2

Приклад. Випадкова величина Х задана щільністю розподілу f ( x ) . Знайти:

1)функцію розподілу F ( x ) , параметр а.

2)математичне сподівання M ( x ), дисперсію D ( x ) , середньоквадратичне

відхилення .

3) моду Mo та медіану Me ;

4)	1
	P		X	2
		2

Побудувати графіки функції та щільність розподілу.

0, при х 0

f ( x ) ax 2 , при 0 х 1

		0, при х	1

Рішення Знайдемо параметр а з рівняння:

f ( x ) dx 1

a 01 x 2 dx 1 , Отже щільність розподілу має вигляд:

a 1 a 3; 3

0, при х 0

f ( x ) 3 x 2 , при 0 х 1

		0, при х	1

Функцію розподілу знайдемо через похідну щільності розподілу:

			0, при	х 0
		3		0 х 1
F ( x ) x			, при
			1, при	х 1
2) математичне сподівання M ( x ), дисперсію D ( x ) , середньоквадратичне
відхилення .
				1	3
M ( X )	x f ( x )dx 3 x 3 dx
					4
				0
Дисперсію знайдемо за формулою:
					1		9				3		9
D ( X )	x 2 f ( x )dx M 2 ( X ) 3 x 4 dx																0,0375
					0		16		5				16
середньоквадратичне відхилення																0,19 .
									0,0375
3) Графіки функцій, мода та медіана

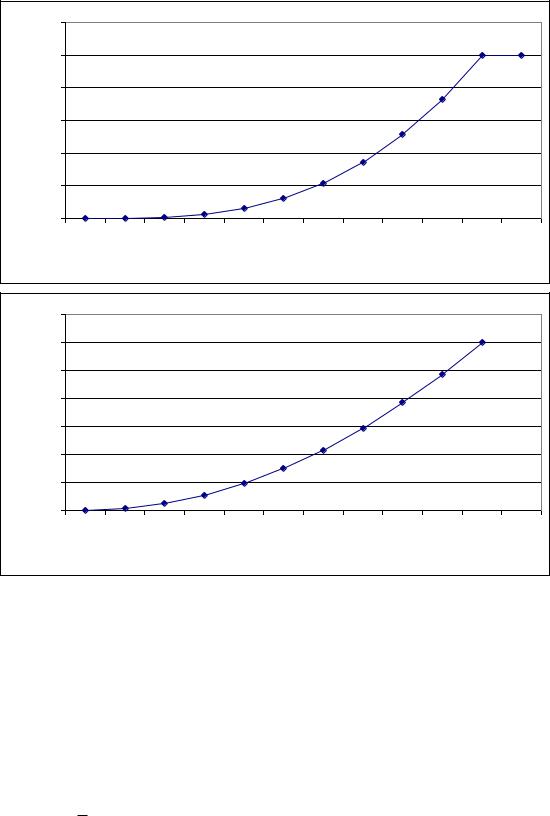
	1,2
	1
	0,8
F(X)	0,6
	0,4
	0,2
	0
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1
							Х

	3,5
	3
	2,5
f(X)	2
	1,5
	1
	0,5
	0
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
							Х
Мода дорівнює 1 (значення найбільшої ймовірності)

Медіану знайдемо з виразу:

	1	b						b b 3		1
			f ( x ) dx x 3								b 0,8
	2	0						0	2
			1	X			F (1)		F (0,5) 1 0,125			0,875
	P					2
			2

Для y 4 x :

0, при х 0

f ( y )			0 х 1
	12 x , при
		0, при	х 1

0, при х 0

F ( y ) 64 x 3 / 2 , при 0 х 1

		1, при х	1

Ширина інтервалу складе: