13 Л е к ц і я № 19

з навчальної дисципліни ”Основи вищої математики та теорії ймовірностей”

напряму підготовки ”Соціологія”

освітньо-кваліфікаційного рівня бакалавр

спеціальності _____________________________________________________

Лекцію розроблено доцентом кафедри ВМ ДУІКТ (2011р) Омецінською О.Б.

Тема: Формула повної ймовірності та формули Байєсса. Повторні випробування за схемою Бернуллі, граничні випадки формули Бернуллі – локальна і інтегральна теореми Лапласа, формула Пуассона. Найпростіший потік подій

Основний зміст

1. Формула повної ймовірності та формули Байєсса.

2. Схема повторних випробувань (схема Бернуллі).

2.1. Найімовірніше число появ випадкової події в схемі Бернуллі.

2.2. Кількість незалежних випробувань, необхідних для настання із заданою імовірністю принаймні однієї події в схемі Бернуллі.

3. Граничні теореми для схеми Бернуллі:

3.1. Локальна теорема Муавра-Лапласа.

3.2. Інтегральна теорема Лапласа. Відхилення відносної частоти від імовірності.

3.3. Гранична теорема Пуассона.

4. Математична модель найпростішого потоку подій.

Текст лекції

1. Формула повної ймовірності та формули Байєсса

Нехай подія А може відбутися тільки за умови настання однієї із попарно несумісних подій В_і (i=1,2,,n), В_iВ_j= при ij, які утворюють повну групу подій в даному випробуванні. Подамо подію А у вигляді суми попарно несумісних подій:

А=(А∩В₁)∪(А∩В₂)∪∪(А∩В_n).

Застосувавши до ймовірності цієї суми Аксіому аддитивності про ймовірність суми попарно несумісних подій, а для ймовірності кожної події-складової – теорему множення ймовірностей залежних подій, дістанемо формулу повної ймовірності події А:

, (1)

де Р(В_і) – імовірність події В_і, Р(А/В_і) – умовна ймовірність настання події А.

Зауваження 1. З аналізу формули (1) випливає, що повна ймовірність Р(А) події А не менша від найменшої і не більша від найбільшої з-посеред її умовних ймовірностей Р(А/В_і), (i=1,2,,n).

А тепер розглянемо події В_і (i=1,2,,n), що утворюють в даному випробувані повну групу попарно несумісних подій. Нехай подія А здійснюється. При цьому ми не можемо з певністю сказати, із якою саме подією із групи випадкових подій В_і (i=1,2,,n) відбулася подія А. Тому події В_і називають гіпотезами. Оскільки гіпотези складають повну групу попарно несумісних подій, то для їхніх ймовірностей справджується рівність

, (2)

Нехай відомі ймовірності гіпотез В_і та умовні ймовірності настання події А, Р(А/В_і), (i=1,2,,n). Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез В_і, тобто знайти умовні ймовірності гіпотез, Р(В_і/А).

Застосуємо теорему множення ймовірностей до залежних подій А, В_і:

Р(А∩В_і)=Р(А)Р(В_і/А)=Р(В_і)Р(А/В_і),

де для Р(А) має місце формула (1). З останнього співвідношення дістанемо формули Байєсса переоцінки ймовірності гіпотез

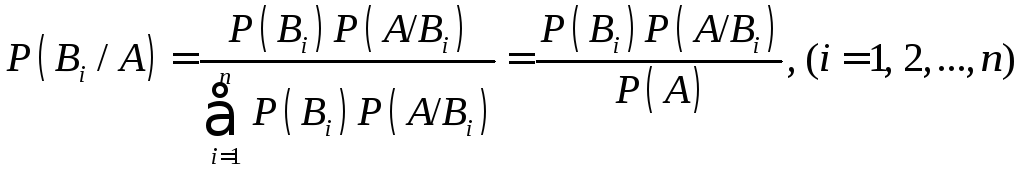. (3)

Формули Байєсса (3) слугують уточненню початкових ймовірностей гіпотез, які досить часто задають на базі статистичної інформації.

Зауваження 2. Після переоцінювання ймовірностей всіх гіпотез для їхніх умовних ймовірностей маємо

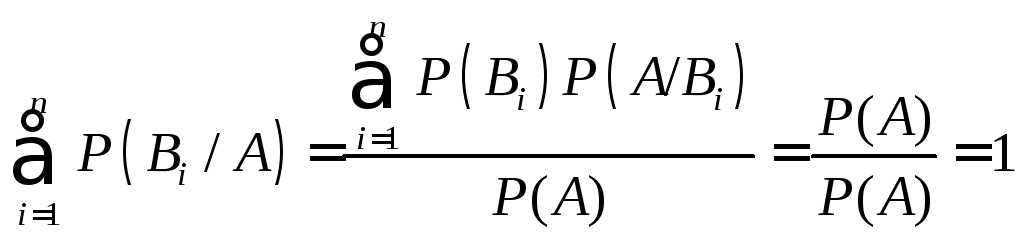, (4)

тобто сума умовних ймовірностей всіх гіпотез дорівнює 1.

Приклад 1. На двох верстатах-автоматах виробляють однакові деталі, які надходять на транспортер. Продуктивність першого верстата втричі більша, ніж другого, причому перший верстат виробляє нестандартну деталь з імовірністю 0,15, а другий — з імовірністю 0,2.

1. Знайти ймовірність того, що навмання взята з транспортера деталь буде стандартною.

2. Виявилось, що навмання взята з транспортера деталь стандартна. Знайти ймовірність того, що цю деталь вироблено на першому верстаті.

 Тут випробування – береться навмання одна деталь. Розглянемо події: В₁ – «деталь виготовлено на першому верстаті»; В₂ – «деталь виготовлено на другому верстаті»; А – «навмання взята деталь є стандартною». Події В₁ і В₂ є несумісними в одному і тому самому випробуванні й утворюють повну групу, що ж до події А, то вона може відбутись із кожною з цих подій-гіпотез. Згідно з умовою задачі продуктивність першого верстата втричі більша, ніж другого, тому Р(В₁)=3/4=0,75, Р(В₂)=1/4=0,25. Умовні ймовірності настання події А відомі: Р(А/В₁)=1-0,15=0,85; Р(А/В₂)=1-0,2=0,8.

1. За формулою повної ймовірності, (1), маємо:

Р(А)=Р(В₁)Р(А/В₁)+Р(В₂)Р(А/В₂)=0,750,85+0,250,8=0,6375+0,2=0,8385.

Відповідь узгоджується із вказаною в Зауваженні 1 властивістю повної ймовірності: 0,8Р(А)0,85.

2. Переоцінимо початкову ймовірність гіпотези В₁, з урахуванням додаткової інформації – навмання взята деталь виявилася стандартною, тобто за умови здійснення події А. Згідно з формулою Байєсса (3) для умовної ймовірності гіпотези В₁ дістанемо:

0,750,85/0,83850,760.

Отже, після переоцінки умовна ймовірність гіпотези В₁ виявилась дещо більшою порівняно з її початковою ймовірністю Р(В₁)=0,75. 

2. Схема повторних випробувань (схема Бернуллі)

Нехай проводяться n випробувань, у кожному з яких подія А може відбутись лише один раз з ймовірністю Р(А)=р або не відбутись з ймовірністю настання протилежної події Оскільки ймовірність р події А у кожному з випробувань однакова, тобто не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називають незалежними щодо події А. Зокрема, такі події мають місце у випадку повторення випробувань. Тому вживають термін – повторні випробування, а також і термін випробування за схемою Бернуллі.

Знайдемо ймовірність Р_n(k) появи події А k разів за проведення n повторних випробувань, 1kn.

Подамо подію А сумою несумісних подій в одному і тому самому складеному випробуванні, яке полягає в проведенні n повторних випробувань:

,

де А_і, і=1,2,n, – поява події А в і-тому випробуванні. Кількість таких подій-складових в записаній сумі дорівнює числу сполучень із n різних елементів по k елементів. Оскільки ймовірність кожної із подій-складових однакова і дорівнює р^kq^n-k, то з урахуванням Аксіоми адитивності про ймовірність суми попарно несумісних подій, дістанемо формулу Бернуллі

; 0≤k≤n, 0!=1. (5)