Лекція 11 державний стандарт україни 4145-2002

Cтандарт ДСТУ 4145-2002 встановлює механізм цифрового підпису, оснований на властивостях групи точок еліптичних кривих над полями характеристики 2, а саме, над полями, де- велике просте число.

11.1 Операції на еліптичних кривих над полями характеристики p≠3

Для невиродженої кривої над полем,, яка задається рівнянням,, комутативний груповий закон з нейтральним елементом(нескінченно віддалена точка) в афінних координатах має наступні властивості:

а) для всіх;

б) якщо , то;для всіх;

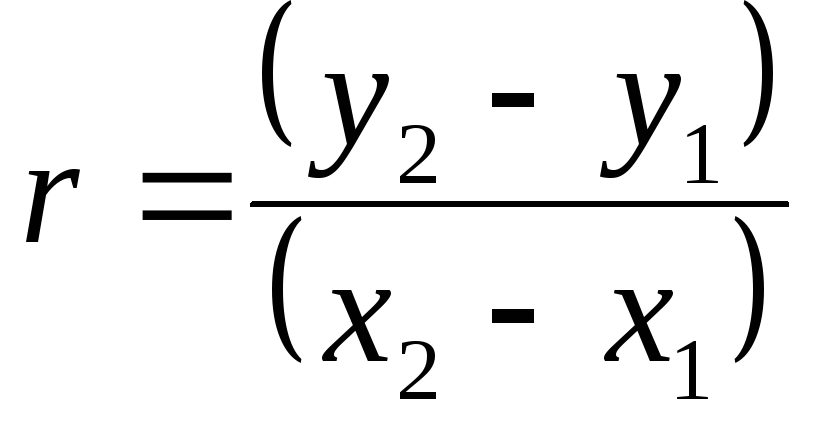в) якщо - скінченні точки, такі, що, і, а, то

, ;

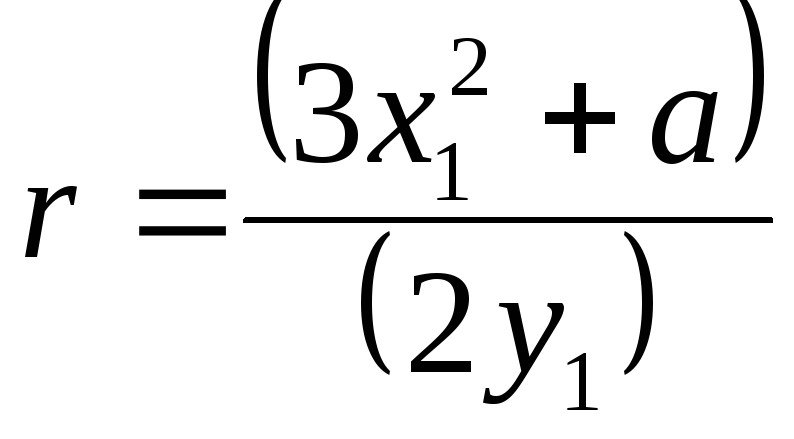г) якщо - скінченні точки,, а, то

, ;

д) Якщо знаменник виразу для дорівнює нулю, то результатом операції на кривій є.

Відомо, що цей алгоритм визначає комутативну і асоціативну групову операцію: (додавання на еліптичній кривій).

Операцію додавання двох однакових точок називають подвоєнням точки.

Опишемо тапер властивості групового закону з нейтральним елементом для невиродженої кривої над полем, яка в ДСТУ 4145-2002 задається рівнянням

, .

Якщо і,- дві точки еліптичної кривої в афінних координатах, то

і .

Крім того, сума точок обчислюється за такими правилами.

для всіх .

Якщо , то. Якщо, то координатиточкиобчислюються за формулами:

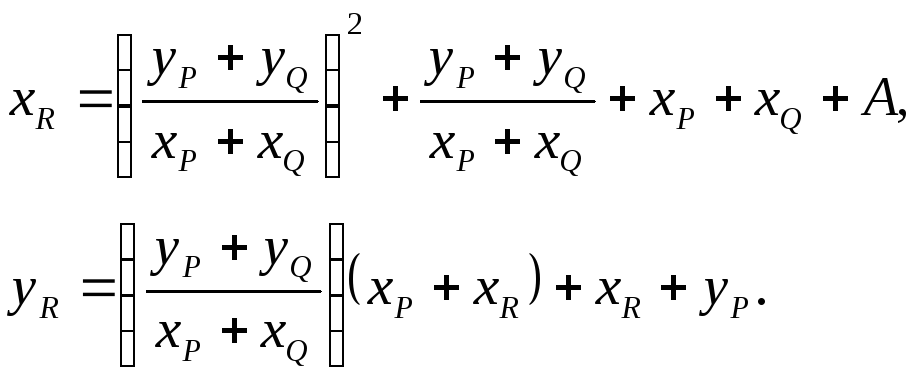
Якщо , то координати подвоєної точкиобчислюються за формулами:

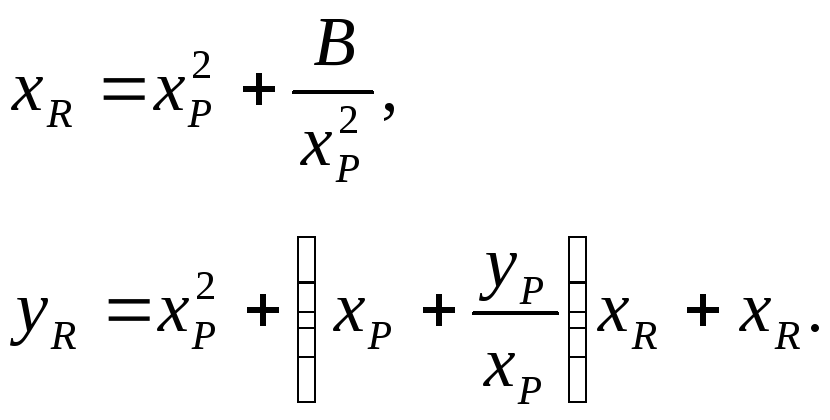
Наприклад, при подвоєнні точки з першою координатою результат приймаємо рівним.

Таким чином, у випадку нулів у знаменнику операції дають .

Якщо записувати - кратне додавання(разів) як, поклавши, то, приі деякому мінімальному значенні, отримаємо, тобто точки кривої утворять циклічну підгрупупорядкагрупи.

Точка називається базовою точкою підгрупи, послідовністьназивається орбітою точки, а число- її порядком. Операціяназивається скалярним множенням. В криптографії використовуються еліптичні криві, які мають підгрупивеликого простого порядку.

Якщо , то у виразікоефіцієнтможна зводити за модулем, а також розглядати вирази видуі, зокрема,, де, тощо.

Таким чином, при обчисленнях на кривій операції з координатами точок проводяться за правилами поля . Якщо знаменник у відповідній формулі дорівнює нулю, то результатом відповідної операції є. При скалярному множенні точок коефіцієнти можна зводити за модулем.

Слід усвідомити, що логіку криптопротоколів на еліптичних кривих легко зрозуміти, виходячи з властивостей скалярного множення, тобто самі формули групових законів для цього не важливі.

11.2 Параметри та формат цифрового підпису

До системних параметрів цифрового підпису належать:

- параметри поля , де- степінь розширення - просте число, а також незвідний поліномстепеня, що визначає операціі в;

- коефіцієнти еліптичної кривої виду , де;

- базова точка еліптичної кривої , що породжує підгрупугрупи;

- порядок базової точки (просте число);

- довжина представлення числау двійковому виді;

- ідентифікатор геш-функції, яка застосовується в мережі ;

- довжина цифрового підпису (довжина блоку даних, що містить цифровий підпис).

Реалізація співвідношень, що задають операції в групі кривої над, суттєво відрізняються від реалізації співвідношень для простого поляхарактеристики.

Наявність полінома ,, необхідна для виконання модульних операцій видунад двійковими векторами коефіціентів поліномів розмірності- елементами.

Всі поліноми , що рекомендовані у стандарті, мають три або п’ять ненульових коефіцієнти і вибрані з урахуванням оптимізації обчислень.

Для множення точки на велике ціле число, як зауважено у стандарті, можна використовувати способи, цілком аналогічні тим, що застосуються для піднесення цілого числа до степеня.

Наприклад, якщо  двійкове зображення числа k, то точку можна обчислити наступним чином:

- присвоїти значення;

- для віддо 0 присвоїти, якщо, інакше, якщо, обчислити.

Однією з особливостей ДСТУ 4145-2002 є можливість застосовувати довільні геш-функції повідомленняз довжиною геш-коду.

Вони розрізняються значенням ідентифікатора . Геш-функції функції, однак, мають узгоджуватися з уповноваженим органом.

Значення геш-кодів розширяється зліва нулями, або частина значущих розрядів зліва відкидається так, щоб довжина геш-коду дорівнювала 256.

За промовченням, без узгодження, а також без ідентифікатора, дозволяється використовувати геш-функцію, встановлену ГОСТ 34.311-95.

Таким чином, ДСТУ 4145-2002 залежить від ГОСТ 28147-89 за рахунок геш-функції, хоча й не так жорстко, як ГОСТ 34.310-95.

Інша особливість полягає у запису цифрового підпису: , а не, який представляється як двійковий рядокD довжини .

До того ж, необхідно, щоб . Таким чином, довжинаможе бути надмірною. Це було зроблено на прохання деяких користувачів, що використовували інший цифровий підпис до введення стандарту в дію.

Для запису ЦП поле розбивається на дві половини у молодших розрядах лівої половини розміщується, аналогічно, у правій половині розміщується. Позиції зайвих бітів заповнюються нулями.

Особистий (секретний) ключ цифрового підпису обчислюють таким чином:

- за визначеною процедурою, обчислюють випадкове ціле число ;

- якщо , то обирають як особистий ключ цифрового підпису, інакше, переходять до попереднього кроку.

Відкритий ключ цифрового підпису обчислюють як точку еліптичної кривої виду , де- базова точка еліптичної кривої.

При формуванні цифрового підпису використовуються рандомізатори.

Важливою особливістю ДСТУ 4145-2002 є те, що в ньому встановлено обов’язкову для використання схему криптографічного генератора псевдовипадкових чисел.

Стандартизація криптографічного генератора є важливим кроком, оскільки тільки з введенням ДСТУ 4145-2002 в дію можна повністю виправдати надійність застосування конкретних рандомізованих цифрових підписів.