Материалы что дал Мухачев / Материалы что дал Мухачев-1 / додаткова_Глава_74

ГЛАВА 74доп.

7.4. Криптосистемы на основе эллиптических кривых

Для построения СОК могут быть использованы эллиптические кривые – математические объекты, определенные над конечными полями [19].

Для случаев характеристик поля , , , алгоритмы вычисления значений, связанных с реализацией подобных СОК, существенно различны. Вместе с тем, основные принципы, на основе которых построены СОК на эллиптических кривых, в идейном смысле одинаковы.

Интересно отметить, что, в отличие от рассмотренных ранее криптосистем, построение открытых параметров для систем на эллиптических кривых является сложной алгоритмической проблемой. В данном случае эффект от стандартизации криптоалгоритмов особенно ощутим.

Для упрощения изложения, рассмотрим эллиптические кривые над простым полем характеристики .

Элиптическая кривая (ЭК) над полем вычетов по модулю непосредственно связана с решениями сравнения , при т.н. условии невырожденности кривой: .

Указанное сравнение называется уравнением кривой в аффинных координатах.

Каждое решение сравнения называется точкой кривой .

Множество решений сравнения можно расширить таким образом, что расширенное множество станет коммутативной группой . Эта группа называется группой точек на эллиптической кривой.

Групповой закон в группе называется сложением. Основной причиной, позволяющей построить группу , является возможность построения новых решений уравнения кривой, исходя из уже известных. Оказывается, если даны решения и то «практически всегда» можно найти третье решение, используя знание координат первых двух.

Операция, сопоставляющая двум (возможно, одинаковым) точкам их «сумму» , в аффинных координатах записывается в виде дробных выражений, поэтому при вычислениях может возникнуть особенность, если в соответствующем знаменателе появится нулевое значение (по модулю ).

Очевидно, это единственная ситуация, когда возникает особенность.

Следовательно, ей можно сопоставить некоторое обозначение () и расширить множество решений уравнения кривой, добавив символ , имитируя тем самым существование дополнительного элемента, называемого бесконечно удаленной точкой.

Можно показать, что если для операции «+» считать нейтральным элементом, то расширенное множество точек кривой превращается в коммутативную группу, а сама операция – в групповой закон.

На самом деле, для аналитического описания расширенного множества точек кривой следует использовать т.н. проективные координаты, в которых точки кривой будут задаваться не парой, а тройкой чисел.

Оказывается, в этом случае все точки кривой будут равноправными и будут подчиняться более общему групповому закону.

Групповой закон в афинных координатах был открыт при исследованиях эллиптических кривых на обычным полем вещественных чисел, что «подсказало» вид соответствующих преобразований над конечными полями.

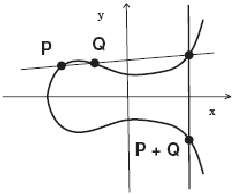
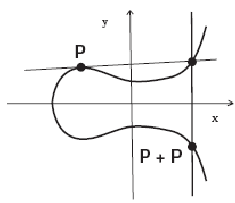
Сложение двух точек ЭК над полем вещественных чисел можно сформулировать в виде геометрического построеня, связывающего координаты точек-слагаемых с координатами точки-суммы (рис.7.2).

Для этого следует учитывать, что если прямая пересекает ЭК в двух точках расширенной кривой, то она пересекает кривую в третьей точке (точка касания считается двойной точкой).

а) б) в)

Рис. 7.2. График эллиптической кривой (а), сложение двух точек (б), кратная точка (в).

Для сложении точек и кривой (рис. 7.2.б) проводим через и прямую. Она пересечет ЭК в некоторой третьей точке . Проведем через прямую, параллельную оси ординат, которая пересечет ЭК в некоторой точке , которую примем за сумму точек кривой: .

Если , то точка является пересечением кривой и касательной к кривой в точке . В соответствующих случаях полагаем, что прямые параллельные оси ординат проходят через бесконечно удаленную точку .

Указанное геометрическое построение называется методом секущих и касательных.

Пусть . Обозначим . Очевидно, что при нашем построении , а . Рассмотрим точку . Пользуясь геометрическим построением, легко проследить, что . Иными словами, прибавление к точке точки эквивалентно «вычитанию» точки из точки . Таким образом, для определения операции вычитания, обратной сложению, положим .

Пусть , и т.д. Исходя из точки , можно построить последовательность точек некоторой длины .

Если записывать подобное -кратное сложение на кривой в виде , положив , то, очевидно, коэффициент можно приводить по модулю и рассматривать выражения вида и . Операция называется скалярным умножением точки на . Наименьшее целое , для которого , называется порядком точки .

Используя аналитическую геометрию, можно показать, что групповой закон соответствует некоторым правилам, которые, в случае конечного поля характеристики , сводятся к следующему.

1. , , где

, если и , если .

2. Если знаменатель обращается в нуль, то .

3. Операция, обратная к сложению:

4. Для любой точки расширенной кривой: .

Как правило, при построении СОК на эллиптической кривой используется точка большого простого порядка . Все операции в СОК осуществляются над точками вида , которые образуют циклическую подгруппу группы .

Покажем, как можно построить аналог алгоритма Диффи-Хеллмана на эллиптической кривой. Исходными параметрами являются сама кривая над конечным полем и точка большого простого порядка .

Пользователи криптосистемы независимо генерируют секретные большие числа и , которые являются параметрами для формирования общего секретного ключа. На их основе вычисляются открытые ключи и .

Произведя обмен открытыми ключами, каждый из абонентов может сформировать общий ключ .

Стойкость СОК основана на сложности задачи дискретного логарифмирования на кривой. Эта задача состоит в нахождении скалярного множителя из соотношения и, в общем случае, является вычислительно недоступной.

Наиболее трудоемким этапом вычисления открытых параметров эллиптической кривой является определение простого числа , которое является делителем количества елементов в группе .

Как правило, вычисление сводится к вычислению с его последующей факторизацией. Для вычисления , вообще говоря, используются сложные алгоритмы. Известны простые ограничения на коеффициенты уравнения ЭК, при которых либо , либо факторизация осуществима.

Теоретически группа состоит из не более, чем двух циклических подгрупп. Обычно параметры кривых таковы, что порядок одной из подгрупп очень мал и определяется сравнительно легко. После чего вычисляется в виде .

Общие алгоритмы вычисления существуют, но являются сложными и трудоемкими.

Для числа имеются оценки. Например, неравенство Хассе: , где – количество элементов в поле характеристики . Таким образом, , где .

Для некоторых кривих число можно вычислить теоретически.

Кривые, для которых называются аномальными, а кривые для которых – суперсингулярными.

Для кривых этих типов известны эффективные методы дискретного логарифмирования.

Тем не менее, сушествует класс криптопротоколов, в которых существенно используются свойства именно суперсингулярных эллиптических кривых.

Интересно отметить, что многие криптографические системы, разработанные на основе системы RSA, порождают аналоги на эллиптических кривых над кольцом вычетов для составного числа , где — различные простые числа.

Эллиптическая кривая над задается теми же алгебраическими уравнениями, что и в случае простого модуля. Например, кривая задается как множество решений основного сравнения , при НОД с бесконечно удаленной точкой .

Операции на выполняются по формулам, соответствующим методу секущих и касательных. К сожалению, такой объект не является группой.

Поэтому вместо рассматривается т.н. прямая сумма кривых : другой объект, который «мало» отличается от .

Каждый елемент – четырехмерный вектор, состоящий из двух точек кривых и .

Если пара удовлетворяет основному сравнению для , то пары вычетов и автоматически удовлетворяют тому же сравнению по модулям и соответственно.

Напомним, что Китайской теоремой об остатках называется следующее утверждение.

Пусть числа попарно взаимно просты и .

Тогда единственное по модулю решение системы сравнений , , имеет вид: , где , .

Действительно, в указанном выражении для слагаемое сравнимо с по модулю , а все прочие сравнимы по этому модулю с нулем.

В силу Китайской теоремы об остатках, и однозначно восстанавливаются по значениям и .

Однако, вместе с бесконечно удаленной точкой , группа содержит совокупность точек вида . Поэтому состоит из точек кривой и некоторого множества особых точек.

Приведем основные свойства , близкие к свойствам , что позволяет строить RSA-подобные криптосистемы.

1. Метод секущих и касательных, в случае, когда он определен для , совпадает с групповой операцией в .

Таким образом, если сложение конкретных точек в выполнимо, то оно выполнимо без факторизации .

2. При больших и , с вероятностью, близкой к единице, умножение точки на скаляр в ведет себя как аналогичная операция в .

Суть этого утверждения в следующем.

Положим НОК. Тогда для подавляющего числа точек и любых целых .

Рассмотрим аналог системы RSA с использованием эллиптической кривой. Открытым ключом является пара , где НОК, , секретным – число , такое, что .

Шифртекст сообщения , которое сопостовляется заранее выбранным способом некоторой точке кривой , отправитель получает спомощью скалярного умножения в виде . Получатель, зная число , восстанавливает .

Оказывается, однако, что сопоставление может потребовать факторизацию , т.е. указанная схема шифрования, вообще говоря, не является корректной. Тем не менее, существует ряд более совершенных RSA-подобных криптосистем, например, криптосистема Демитко (для кривых общего вида), либо криптосистема Кувакадо-Кояма для кривых вида .