Материалы что дал Мухачев / Материалы что дал Мухачев-1 / Consp_Lect_Fields

Скінченні поля і многочлени над полями

Полем називається множина 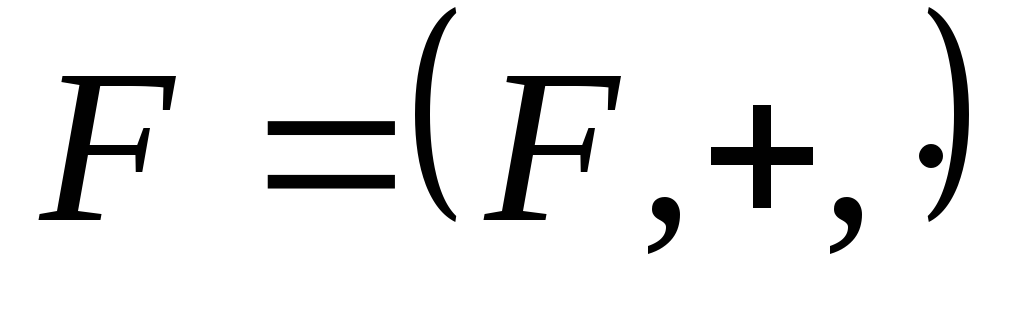з двома операціями, що називаються додаванням і множенням і для якої виконуються наступні аксіоми.

1. Кількість елементів у - не менше двох.

2.Асоциативнось додавання: .

3. Комутативность додавання: .

4. Розв’язність рівняння для усіх

5. Асоциативнось для множення: .

6. Комутативність для множення:

7. Дистрибутивний закон: .

8. Розв’язність рівняння для усіх , при .

Можна довести, що з аксіом випливає наявність нейтрального елемента 0 (нуля) для операції додавання, а також нейтрального елемента 1 (одиниці) для множення, при цьому .

Крім того доводяться звичайні правила операцій: , , тощо.

Існує тільки один розвязок рівняння при . Він позначається через .

Зауваження. Нехай . Тоді результатом ділення елемента на елемент називається операція .

Зауваження. Якщо і , то, принаймні, один з елементів дорівнює нулю. Приклад (дільники нуля): , це означає, що цільце лишків за модулем 6 не є полем.

Таки дільники існують завжди, якщо модуль – складене число.

Приклади полів: поле раціональних дробів , дійсних чисел і поле комплексних чисел . Очевидно, . Говорять, що є підполем (крім того, підполем поля ). З іншого боку, поля і називаються надполями або розширеннями поля .

Поле, що не є надполем ні для яких підполей називається простим (наприклад, поле раціональних чисел - просте).

Існують поля, що складаються зі скінченного числа елементів. Такі поля називаються полями Галуа.

Поле Галуа, що складається з елементів, позначається або . Додавання у полі має фундаментальну особливість: існує число таке, що результат додавання будь-якого елемента поля раз самим із собою дорівнює нулю.

Число називається характеристикою поля, якщо сума, що складається з одиниць дорівнює нулю і - мінімальне число з такою властивістю.

Характеристика поля позначається .

Поле такої властивості не має. У подібних випадках характеристика поля вважається рівною нулю: .

Можна довести, що:

- характеристика скінченного поля обов’язково є простим числом.

- для кожного простого числа існує просте поле характеристики , напр. кільце лишків за модулем (поле – частковий випадок комутативного кільця).

Виявляється, що число елементів довільного скінченного поля завжди є степенем деякого простого числа , що є його характеристікою: , тобто , ,

Число називається степенем розширення поля.

Мала теорема Ферма. Нехай множина ненулевих елементів поля .

, (теж саме, що , , але останне вірно також для ).

Можна довести, що у полі завжди знайдеться елемент , такий, що існує число : . Елемент називається генератором, або первісним елементом поля. Первісних елементів у полі багато, але знайти первісний елемент для великих полів вдається рідко.

Можна показати, що . Тобто і тому всі поля є розширеннями поля . Можна довести, що - просте поле, а всі нескінченні поля є розширеннями простого поля .

Многочлени над полем.

Многочлен над полем - це функція виду , де , . (, ).

Ціле число називається степенем многочлена і позначається . Многочлен степеня має коефіціент. Аналогічно визначається многочлен над комутативним кільцем. Множина усіх многочленів від однієї змінної над комутативним кільцем також є комутативним кільцем. Якщо , по многочлен називається зведеним (нормованим, унітарним). Многочлен називається дільником многочлена , , якщо існує многочлен , такий, що , і степені многочленів більші нуля.

Спільним дільником двох многочленів називається многочлен, що ділить обидва зазначені многочлени. таким чином, дільники многочленів визначаються з точністю до константи.

Найбільшим спільним дільником двох многочленів називається многочлен , такий, що будь-який спільний дільник многочленів і ділить .

Звичайно, в якості вибирається нормований многочлен.

Визначення. Многочлен ненульового степеня називається незвідним, якщо він ділиться тільки на константи і сам на себе.

Незвідний нормований многочлен степеня над полем можна використовувати для побудови розширення . У цьому випадку називається породжуючим поліномом поля. Породжуючий поліном називається примітивним, якщо один з первісних елементів полі має спеціальний вид (див. далі).

Деяки властивості розширень наступні.

1. є -вимірним лінійним векторним простором над полем і містить елементів (векторів) розмірності , координати яких є лишками за модулем .

2. Таким чином, при додаванні векторів у координати додаються за модулем .

3. Для добутку у векторів виду , , де координати – довільні лишки за модулем , виконуємо наступні операції.

3.1. Переходімо від векторів до многочленів: , , де , та знаходимо їхній добуток , який може бути многочленом степеня вище .

3.2. Знаходимо лишок , тобто залишок від ділиння на виду , де при відсутніх степенях змінної проставляємо нульові коефіціенти (очевидно, степінь не перевищує ).

3.3. Записуємо , де вектор відповідає .

4. У полі елементи підполя є «розширеними», тобто мають вид , , , , відповідно. Вони відповідають многочленам степеня нуль. Очевидно, результати суми і добутку цих елементів за правилами розширеного поля не виводять результати з їхньої множини, а самі результати можна також отримати за правилами поля, що виконуються лише над останніми координатими векторів. У цьому сенсі операції у полі діють на елементи підполя так само, як «старі» операції у підполі.

Зауваження. При записі алгебраїчних виразів для розширених елементів деколи застосовують запис виду .

Обернений елемент до вектора визначається як вектор , що задовільняє умову . Таким чином, .

Обчислення проводиться за алгоритмом Евкліда, аналогічно до побудови найбільшого спільного дільника чисел (вважаємо далі ).

1.	Розміщуємо 25, 15 і одиничну матрицю		25
			15
2	Ділимо (у стовбчику ) 25 на 15, Записуємо частку і залишок: 25=1·15+10. Задіємо два попередні рядки: частку множимо на елемент, що помічений однією крапкою і результат віднімаємо від єлемента, що помічений двома крапками: 1- 0·1=1. Результат записуємо у стовбчик . Аналогічно, 0-1·1=-1, записуємо у стовбчик .	1 частка	10 залишок		-1
3	Аналогічно, ділимо 15 на 10, Записуємо частку і залишок: У стовбчик записуємо 0-1·1=-1, а у стовбчик 1-1· (-1)=2	1 частка	5 залишок	-1	2
4.	Ділимо на , залишок – нуль. Виписуємо результат з попереднього рядка: .	2 частка	залишок

Перевіримо

Обчислимо . За алгоритмом, для виразу отримаємо . Зводимо ліву частину за модулем 25 і бачимо, що , тобто .

Для обчислення можна застосувати аналогічну схему, яку пояснимо для поля . У нас , тому породжуючий поліном буде мати степінь 3, скажимо (цей поліном незвідний на полем ). Поле містить 8 тримірних векторів. Знайдемо для . Очевидно, .

1.	Розміщуємо , і одиничну матрицю
2	Ділимо (у стовбчику ) на , Записуємо частку і залишок: . Частку множимо на елемент, що помічений однією крапкою і результат віднімаємо від єлемента, що помічений двома крапками: . Результат записуємо у стовбчик . Аналогічно, записуємо у стовбчик .	частка	залишок
3	Ділимо на , Записуємо частку і залишок: . У стовбчик записуємо , а у стовбчик -	частка	залишок
4.	Ділимо на , залишок – нуль. Виписуємо результат з попереднього кроку.	частка	залишок

Результат означає, що НСД і .

Остання рівність за модулем дає , тобто і .

Таблиця 1 Обернені елементи у полі

	001	010	011	100	101	110	111
	001	101	110	111	010	011	100